Hessian polyhedron

In geometry, the Hessian polyhedron is a regular complex polyhedron ₃{3}₃{3}₃, , in ${\displaystyle \mathbb {C} ^{3}}$. It has 27 vertices, 72 ₃{} edges, and 27 ₃{3}₃ faces. It is self-dual.

Hessian polyhedron
Orthographic projection (triangular 3-edges outlined as black edges)
Schläfli symbol	3{3}3{3}3
Coxeter diagram
Faces	27 3{3}3
Edges	72 3{}
Vertices	27
Petrie polygon	Dodecagon
van Oss polygon	12 3{4}2
Shephard group	L3 = 3[3]3[3]3, order 648
Dual polyhedron	Self-dual
Properties	Regular

Coxeter named it after Ludwig Otto Hesse for sharing the Hessian configuration ${\displaystyle \left[{\begin{smallmatrix}9&4\\3&12\end{smallmatrix}}\right]}$ or (9₄12₃), 9 points lying by threes on twelve lines, with four lines through each point.[1]

Its complex reflection group is ₃[3]₃[3]₃ or , order 648, also called a Hessian group. It has 27 copies of , order 24, at each vertex. It has 24 order-3 reflections. Its Coxeter number is 12, with degrees of the fundamental invariants 3, 6, and 12, which can be seen in projective symmetry of the polytopes.

The Witting polytope, ₃{3}₃{3}₃{3}₃, contains the Hessian polyhedron as cells and vertex figures.

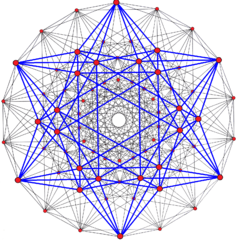
It has a real representation as the 2₂₁ polytope, , in 4-dimensional space, sharing the same 27 vertices. The 216 edges in 2₂₁ can be seen as the 72 ₃{} edges represented as 3 simple edges.

Coordinates

Its 27 vertices can be given coordinates in ${\displaystyle \mathbb {C} ^{3}}$: for (λ, μ = 0,1,2).

(0,ω^λ,−ω^μ)

(−ω^μ,0,ω^λ)

(ω^λ,−ω^μ,0)

where ${\displaystyle \omega ={\tfrac {-1+i{\sqrt {3}}}{2}}}$.

As a Configuration

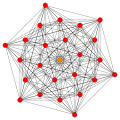
Hessian polyhedron with triangular 3-edges outlined as black edges, with one face outlined as blue.

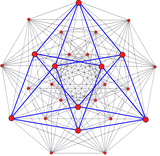One of 12 Van oss polygons, 3{4}2, in the Hessian polyhedron

Its symmetry is given by ₃[3]₃[3]₃ or , order 648.[2]

The configuation matrix for ₃{3}₃{3}₃ is:[3]

${\displaystyle \left[{\begin{smallmatrix}27&8&8\\3&72&3\\8&8&27\end{smallmatrix}}\right]}$

The number of k-face elements (f-vectors) can be read down the diagonal. The number of elements of each k-face are in rows below the diagonal. The number of elements of each k-figure are in rows above the diagonal.

L3		k-face	fk	f0	f1	f2	k-fig	Notes
L2		( )	f0	27	8	8	3{3}3	L3/L2 = 27*4!/4! = 27
L1L1		3{ }	f1	3	72	3	3{ }	L3/L1L1 = 27*4!/9 = 72
L2		3{3}3	f2	8	8	27	( )	L3/L2 = 27*4!/4! = 27

Images

These are 8 symmetric orthographic projections, some with overlapping vertices, shown by colors. Here the 72 triangular edges are drawn as 3-separate edges.

Coxeter plane orthographic projections

E6 [12]	Aut(E6) [18/2]	D5 [8]	D4 / A2 [6]
(1=red,3=orange)	(1)	(1,3)	(3,9)
B6 [12/2]	A5 [6]	A4 [5]	A3 / D3 [4]
(1,3)	(1,3)	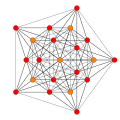(1,2)	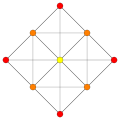(1,4,7)

Related complex polyhedra

Double Hessian polyhedron
Schläfli symbol	2{4}3{3}3
Coxeter diagram
Faces	72 2{4}3
Edges	216 {}
Vertices	54
Petrie polygon	Octadecagon
van Oss polygon	{6}
Shephard group	M3 = 3[3]3[4]2, order 1296
Dual polyhedron	Rectified Hessian polyhedron, 3{3}3{4}2
Properties	Regular

The Hessian polyhedron can be seen as an alternation of , = . This double Hessian polyhedron has 54 vertices, 216 simple edges, and 72 faces. Its vertices represent the union of the vertices and its dual .

Its complex reflection group is ₃[3]₃[4]₂, or , order 1296. It has 54 copies of , order 24, at each vertex. It has 24 order-3 reflections and 9 order-2 reflections. Its coxeter number is 18, with degrees of the fundamental invariants 6, 12, and 18 which can be seen in projective symmetry of the polytopes.

Coxeter noted that the three complex polytopes , , resemble the real tetrahedron (), cube (), and octahedron (). The Hessian is analogous to the tetrahedron, like the cube is a double tetrahedron, and the octahedron as a rectified tetrahedron. In both sets the vertices of the first belong to two dual pairs of the second, and the vertices of the third are at the center of the edges of the second.[4]

Its real representation 54 vertices are contained by two 2₂₁ polytopes in symmetric configurations: and . Its vertices can also be seen in the dual polytope of 1₂₂.

Construction

The elements can be seen in a configuration matrix:

M3		k-face	fk	f0	f1	f2	k-fig	Notes
L2		( )	f0	54	8	8	3{3}3	M3/L2 = 1296/24 = 54
L1A1		{ }	f1	2	216	3	3{ }	M3/L1A1 = 1296/6 = 216
M2		2{4}3	f2	6	9	72	( )	M3/M2 = 1296/18 = 72

Images

Orthographic projections

polyhedron

polyhedron with one face, 2{4}3 highlighted blue

polyhedron with 54 vertices, in two 2 alternate color

and , shown here with red and blue vertices form a regular compound

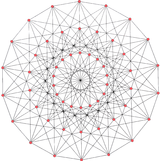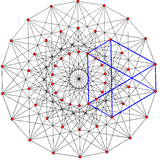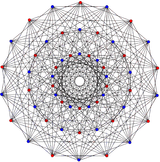Rectified Hessian polyhedron

Rectified Hessian polyhedron
Schläfli symbol	3{3}3{4}2
Coxeter diagrams	or .
Faces	54 3{3}3
Edges	216 3{}
Vertices	72
Petrie polygon	Octadecagon
van Oss polygon	9 3{4}3
Shephard group	M3 = 3[3]3[4]2, order 1296 3[3]3[3]3, order 648
Dual polyhedron	Double Hessian polyhedron 2{4}3{3}3
Properties	Regular

The rectification, doubles in symmetry as a regular complex polyhedron with 72 vertices, 216 ₃{} edges, 54 ₃{3}₃ faces. Its vertex figure is ₃{4}₂, and van oss polygon ₃{4}₃. It is dual to the double Hessian polyhedron.[5]

It has a real representation as the 1₂₂ polytope, , sharing the 72 vertices. Its 216 3-edges can be drawn as 648 simple edges, which is 72 less than 1₂₂'s 720 edges.

or has 72 vertices, 216 3-edges, and 54 3{3}3 faces

with one blue face, 3{3}3 highlighted

with one of 9 van oss polygon, 3{4}3, highlighted

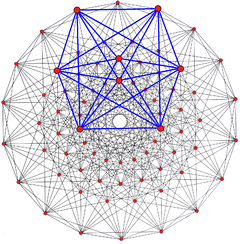Construction

The elements can be seen in two configuration matrices, a regular and quasiregular form.

M₃ = ₃[3]₃[4]₂ symmetry

M3		k-face	fk	f0	f1	f2	k-fig	Notes
	( )	f0	72	9	6	3{4}2	M3/M2 = 1296/18 = 72
L1A1		3{ }	f1	3	216	2	{ }	M3/L1A1 = 1296/3/2 = 216
L2		3{3}3	f2	8	8	54	( )	M3/L2 = 1296/24 = 54

L₃ = ₃[3]₃[3]₃ symmetry

L3		k-face	fk	f0	f1	f2		k-fig	Notes
L1L1		( )	f0	72	9	3	3	3{ }×3{ }	L3/L1L1 = 648/9 = 72
L1		3{ }	f1	3	216	1	1	{ }	L3/L1 = 648/3 = 216
L2		3{3}3	f2	8	8	27	*	( )	L3/L2 = 648/24 = 27
				8	8	*	27

References

1. Coxeter, Complex Regular polytopes, p.123
2. Coxeter Regular Convex Polytopes, 12.5 The Witting polytope
3. Coxeter, Complex Regular polytopes, p.132
4. Coxeter, Complex Regular Polytopes, p.127
5. Coxeter, H. S. M., Regular Complex Polytopes, second edition, Cambridge University Press, (1991). p.30 and p.47

• Coxeter, H. S. M. and Moser, W. O. J.; Generators and Relations for Discrete Groups (1965), esp pp 67–80.
• Coxeter, H. S. M.; Regular Complex Polytopes, Cambridge University Press, (1974).
• Coxeter, H. S. M. and Shephard, G.C.; Portraits of a family of complex polytopes, Leonardo Vol 25, No 3/4, (1992), pp 239–244,