Witting polytope

In 4-dimensional complex geometry, the Witting polytope is a regular complex polytope, named as: ₃{3}₃{3}₃{3}₃, and Coxeter diagram . It has 240 vertices, 2160 ₃{} edges, 2160 ₃{3}₃ faces, and 240 ₃{3}₃{3}₃ cells. It is self-dual. Each vertex belongs to 27 edges, 72 faces, and 27 cells, corresponding to the Hessian polyhedron vertex figure.

Witting polytope
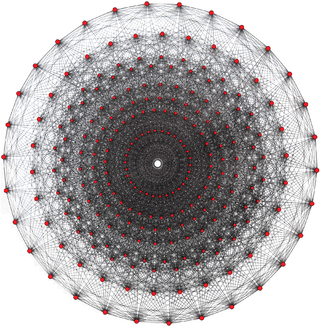Schläfli symbol	3{3}3{3}3{3}3
Coxeter diagram
Cells	240 3{3}3{3}3
Faces	2160 3{3}3
Edges	2160 3{}
Vertices	240
Petrie polygon	30-gon
van Oss polygon	90 3{4}3
Shephard group	L4 = 3[3]3[3]3[3]3, order 155,520
Dual polyhedron	Self-dual
Properties	Regular

Symmetry

Its symmetry by ₃[3]₃[3]₃[3]₃ or , order 155,520.[1] It has 240 copies of , order 648 at each cell.[2]

Structure

The configuration matrix is:[3] ${\displaystyle \left[{\begin{smallmatrix}240&27&72&27\\3&2160&8&8\\8&8&2160&3\\27&72&27&240\end{smallmatrix}}\right]}$

The number of vertices, edges, faces, and cells are seen in the diagonal of the matrix. These are computed by the order of the group divided by the order of the subgroup, by removing certain complex reflections, shown with X below. The number of elements of the k-faces are seen in rows below the diagonal. The number of elements in the vertex figure, etc, are given in rows above the digonal.

L4		k-face	fk	f0	f1	f2	f3	k-figure	Notes
L3		( )	f0	240	27	72	27	3{3}3{3}3	L4/L3 = 216*6!/27/4! = 240
L2L1		3{ }	f1	3	2160	8	8	3{3}3	L4/L2L1 = 216*6!/4!/3 = 2160
		3{3}3	f2	8	8	2160	3	3{ }
L3		3{3}3{3}3	f3	27	72	27	240	( )	L4/L3 = 216*6!/27/4! = 240

Coordinates

Its 240 vertices are given coordinates in ${\displaystyle \mathbb {C} ^{4}}$:

(0, ±ω^μ, -±ω^ν, ±ω^λ) (-±ω^μ, 0, ±ω^ν, ±ω^λ) (±ω^μ, -±ω^ν, 0, ±ω^λ) (-±ω^λ, -±ω^μ, -±ω^ν, 0)

(±ω^λ√3, 0, 0, 0) (0, ±ω^λ√3, 0, 0) (0, 0, ±ω^λ√3, 0) (0, 0, 0, ±ω^λ√3)

where ${\displaystyle \omega ={\tfrac {-1+i{\sqrt {3}}}{2}},\lambda ,\nu ,\mu =0,1,2}$.

The last 6 points form hexagonal holes on one of its 40 diameters. There are 40 hyperplanes contain central ₃{3}₃{4}₂, figures, with 72 vertices.

Witting configuration

Coxeter named it after Alexander Witting for being a Witting configuration in complex projective 3-space:[4]

${\displaystyle \left[{\begin{smallmatrix}40&12&12\\2&240&2\\12&12&40\end{smallmatrix}}\right]}$ or ${\displaystyle \left[{\begin{smallmatrix}40&9&12\\4&90&4\\12&9&40\end{smallmatrix}}\right]}$

The Witting configuration is related to the finite space PG(3,2²), consisting of 85 points, 357 lines, and 85 planes.[5]

Related real polytope

Its 240 vertices are shared with the real 8-dimensional polytope 4₂₁, . Its 2160 3-edges are sometimes drawn as 6480 simple edges, slightly less than the 6720 edges of 4₂₁. The 240 difference is accounted by 40 central hexagons in 4₂₁ whose edges are not included in ₃{3}₃{3}₃{3}₃.[6]

The honeycomb of Witting polytopes

The regular Witting polytope has one further stage as a 4-dimensional honeycomb, . It has the Witting polytope as both its facets, and vertex figure. It is self-dual, and its dual coincides with itself.[7]

Hyperplane sections of this honeycomb include 3-dimensional honeycombs .

The honeycomb of Witting polytopes has a real representation as the 8-dimensional polytope 5₂₁, .

Its f-vector element counts are in proportion: 1, 80, 270, 80, 1.[8] The configuration matrix for the honeycomb is:

L5		k-face	fk	f0	f1	f2	f3	f4	k-figure	Notes
L4		( )	f0	N	240	2160	2160	240	3{3}3{3}3{3}3	L5/L4 = N
L3L1		3{ }	f1	3	80N	27	72	27	3{3}3{3}3	L5/L3L1 = 80N
L2L2		3{3}3	f2	8	8	270N	8	8	3{3}3	L5/L2L2 = 270N
L3L1		3{3}3{3}3	f3	27	72	27	80N	3	3{}	L5/L3L1 = 80N
L4		3{3}3{3}3{3}3	f4	240	2160	2160	240	N	( )	L5/L4 = N

Notes

1. Coxeter Regular Convex Polytopes, 12.5 The Witting polytope
2. Coxeter, Complex Regular Polytopes, p.134
3. Coxeter, Complex Regular polytopes, p.132
4. Alexander Witting, Ueber Jacobi'sche Functionen k^ter Ordnung Zweier Variabler, Mathemematische Annalen 29 (1887), 157-70, see especially p.169
5. Coxeter, Complex regular polytopes, p.133
6. Coxeter, Complex Regular Polytopes, p.134
7. Coxeter, Complex Regular Polytopes, p.135
8. Coxeter Regular Convex Polytopes, 12.5 The Witting polytope

References

• Coxeter, H. S. M. and Moser, W. O. J.; Generators and Relations for Discrete Groups (1965), esp pp 67–80.
• Coxeter, H. S. M.; Regular Complex Polytopes, Cambridge University Press, second edition (1991). pp. 132–5, 143, 146, 152.
• Coxeter, H. S. M. and Shephard, G.C.; Portraits of a family of complex polytopes, Leonardo Vol 25, No 3/4, (1992), pp 239–244