Gauss iterated map

In mathematics, the Gauss map (also known as Gaussian map[1] or mouse map), is a nonlinear iterated map of the reals into a real interval given by the Gaussian function:

${\displaystyle x_{n+1}=\exp(-\alpha x_{n}^{2})+\beta ,\,}$

Cobweb plot of the Gauss map for ${\displaystyle \alpha =4.90}$ and ${\displaystyle \beta =-0.58}$. This shows an 8-cycle.

where α and β are real parameters.

Named after Johann Carl Friedrich Gauss, the function maps the bell shaped Gaussian function similar to the logistic map.

Properties

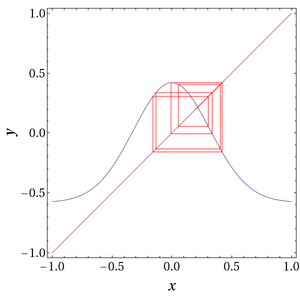
In the parameter real space ${\displaystyle x_{n}}$ can be chaotic. The map is also called the mouse map because its bifurcation diagram resembles a mouse (see Figures).

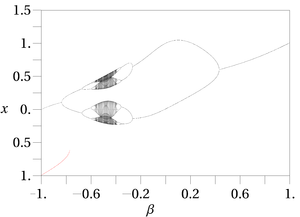Bifurcation diagram of the Gauss map with ${\displaystyle \alpha =4.90}$ and ${\displaystyle \beta }$ in the range −1 to +1. This graph resembles a mouse.

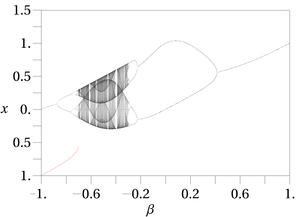Bifurcation diagram of the Gauss map with ${\displaystyle \alpha =6.20}$ and ${\displaystyle \beta }$ in the range −1 to +1.

References

1. Chaos and nonlinear dynamics: an introduction for scientists and engineers, by Robert C. Hilborn, 2nd Ed., Oxford, Univ. Press, New York, 2004.