Enharmonic

In modern musical notation and tuning, an enharmonic equivalent is a note, interval, or key signature that is equivalent to some other note, interval, or key signature but "spelled", or named differently. Thus, the enharmonic spelling of a written note, interval, or chord is an alternative way to write that note, interval, or chord.

Not to be confused with Anharmonic or Inharmonic.
Comparison of intervals near or enharmonic with the unison

Definition

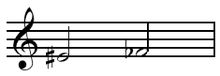
For example, in twelve-tone equal temperament (the currently predominant system of musical tuning in Western music), the notes C♯ and D♭ are enharmonic (or enharmonically equivalent) notes. Namely, they are the same key on a keyboard, and thus they are identical in pitch, although they have different names and different roles in harmony and chord progressions. Arbitrary amounts of accidentals can produce further enharmonic equivalents, such as B (meaning B double sharp), although these are much rarer and have less practical use.

In other words, if two notes have the same pitch but have different letter names, we call them enharmonic.[1] "Enharmonic intervals are intervals with the same sound that are spelled differently… [resulting], of course, from enharmonic tones."[2]

Prior to this modern meaning, "enharmonic" referred to notes that were very close in pitch—closer than the smallest step of a diatonic scale—but not identical in pitch. One such example is F♯, which is not the same note and sound as G♭ in many non-12-equal tempered tunings,[3] as in an enharmonic scale. "Enharmonic equivalence is peculiar to post-tonal theory."[4] "Much music since at least the 18th century, however, exploits enharmonic equivalence for purposes of modulation and this requires that enharmonic equivalents in fact be equivalent."[5]

The notes F♯ and G♭ are enharmonic equivalents.
E♯ and F♭, however, are not enharmonic equivalents, because E♯ is enharmonic with F♮.
G and B are enharmonic equivalents, both the same as A♮.
Enharmonically equivalent key signatures of B♮ and C♭ major, each followed by its respective tonic chord

Some key signatures have an enharmonic equivalent that represents a scale identical in sound but spelled differently. The number of sharps and flats of two enharmonically equivalent keys sum to twelve. For example, the key of B major, with 5 sharps, is enharmonically equivalent to the key of C♭ major with 7 flats, and 5 (sharps) + 7 (flats) = 12. Keys past 7 sharps or flats exist only theoretically and not in practice. The enharmonic keys are six pairs, three major pairs and three minor pairs: B major/C♭ major, G♯ minor/A♭ minor, F♯ major/G♭ major, D♯ minor/E♭ minor, C♯ major/D♭ major and A♯ minor/B♭ minor. There are practically no works composed in keys that require double sharps or double flats in the key signature. In practice, musicians learn and practice 15 major and 15 minor keys, three more than 12 due to the enharmonic spellings.

Enharmonic equivalents can also be used to improve the readability of a line of music. For example, a sequence of notes is more easily read as "ascending" or "descending" if the noteheads are on different positions on the staff. Doing so may also reduce the number of accidentals that must be used. Thus, in the key of B♭ major, the sequence B♭-B♮-B♭ is more easily read using the enharmonic spelling C♭ instead of B♮.

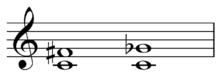
Enharmonic tritones: augmented 4th = diminished 5th on C Play .

For example, the intervals of a minor sixth on C, on B♯, and an augmented fifth on C are all enharmonic intervals Play . The most common enharmonic intervals are the augmented fourth and diminished fifth, or tritone, for example C–F♯ = C–G♭.[1]

Enharmonic equivalence is not to be confused with octave equivalence, nor are enharmonic intervals to be confused with inverted or compound intervals.

Examples in practice

A particularly ingenious example in popular music occurs in melody line of Jerome Kern's song “All the things you are”, where the note G sharp that concludes the bridge section repeats, over changing harmony, as an A flat, the first note of the returning “A” section. [6][7]

Beethoven's Piano Sonata in E minor, Op. 90, contains a passage where the lowest note, B-flat, becomes an A-sharp, altering its musical meaning and significance. The first two bars of the following passage unfold a simple descending scale of B-flat major. However, according to Wilfrid Mellers, the B-flats here "turn out to be a pun, for they change enharmonically into A-sharps, part of a dominant ninth leading to B minor."[8]

Beethoven Sonata in E minor Op 90, first movement, bars 37–45

Chopin's Prelude No. 15, known as the "Raindrop Prelude", features a pedal point on the note A-flat throughout its opening section.

Chopin Prelude No. 15, opening

"The repeated A-flats ... become enharmonically changed into G-sharps in the middle section of this Prelude, and take on a brooding, ominous character."[9]

Chopin Prelude No. 15, bars 28–29

One of the most spectacular enharmonic changes in all music occurs in the concluding passage of the slow movement of one of Schubert's last sonatas, his final piano sonata, in B-flat, D960. Here, the note B-sharp transforms into C natural as part of a progression from the chord of G-sharp (within they key of C-sharp minor) to the chord of C major:

G-sharp to C progression

The effect, in the context of the passage as a whole, (bars 102–103) is magical:

Schubert Piano Sonata D960 second movement, bars 98–106

According to pianist Paul Lewis:

As you come into this last page, there's a sense of reaching out for something that you can't quite reach, that you can't quite get. When you get to the top, you haven't got it — but there's a breathing out, an accepting that that's how it is. Then, to go from C-sharp minor into this unbelievable C-sharp major moment in triple piano. When Schubert uses the major like that, it's anything but a resolution. It's not a reassurance, either. It's not that everything is going to be all right — nothing is going to be all right. It's just about accepting the way things are. That's so Schubertian as an idea, and it's so wonderfully conveyed in this page.[10]

Tuning enharmonics

In principle, the modern musical use of the word enharmonic to mean identical tones is correct only in equal temperament, where the octave is divided into 12 equal semitones. In other tuning systems, however, enharmonic associations can be perceived by listeners and exploited by composers.[11]

Pythagorean
Main article: Pythagorean tuning

In Pythagorean tuning, all pitches are generated from a series of justly tuned perfect fifths, each with a frequency ratio of 3 to 2. If the first note in the series is an A♭, the thirteenth note in the series, G♯ is higher than the seventh octave (octave = ratio of 1 to 2, seven octaves is 1 to 27 = 128) of the A♭ by a small interval called a Pythagorean comma. This interval is expressed mathematically as:

Meantone
Main article: Meantone temperament

In quarter-comma meantone, on the other hand, consider G♯ and A♭. Call middle C's frequency x. Then high C has a frequency of 2x. The quarter-comma meantone has just (i.e., perfectly-tuned) major thirds, which means major thirds with a frequency ratio of exactly 4 to 5.

To form a just major third with the C above it, A♭ and high C must be in the ratio 4 to 5, so A♭ needs to have the frequency

To form a just major third above E, however, G♯ needs to form the ratio 5 to 4 with E, which, in turn, needs to form the ratio 5 to 4 with C. Thus the frequency of G♯ is

Thus, G♯ and A♭ are not the same note; G♯ is, in fact 41 cents lower in pitch (41% of a semitone, not quite a quarter of a tone). The difference is the interval called the enharmonic diesis, or a frequency ratio of 128/125. On a piano tuned in equal temperament, both G♯ and A♭ are played by striking the same key, so both have a frequency

Such small differences in pitch can escape notice when presented as melodic intervals. However, when they are sounded as chords, the difference between meantone intonation and equal-tempered intonation can be quite noticeable, even to untrained ears.

One can label enharmonically equivalent pitches with one and only one name; for instance, the numbers of integer notation, as used in serialism and musical set theory and employed by the MIDI interface.

Enharmonic genus
Main article: Genus (music) § Enharmonic

In ancient Greek music the enharmonic was one of the three Greek genera in music in which the tetrachords are divided (descending) as a ditone plus two microtones. The ditone can be anywhere from 16/13 to 9/7 (3.55 to 4.35 semitones) and the microtones can be anything smaller than 1 semitone.[12] Some examples of enharmonic genera are

  1. 1/1 36/35 16/15 4/3
  2. 1/1 28/27 16/15 4/3
  3. 1/1 64/63 28/27 4/3
  4. 1/1 49/48 28/27 4/3
  5. 1/1 25/24 13/12 4/3
gollark: Not a language feature.
gollark: It would make more sense as a macro.
gollark: I like it not.
gollark: ah.
gollark: Did they not already exist?

See also

Sources
  1. Benward, Bruce; Saker, Marilyn (2003). Music in Theory and Practice. I. p. 7 & 360. ISBN 978-0-07-294262-0.
  2. Benward, Bruce; Saker, Marilyn (2003). Music in Theory and Practice. I. p. 54. ISBN 978-0-07-294262-0.
  3. Elson, Louis Charles (1905). Elson's Music Dictionary. O. Ditson Company. p. 100. The relation existing between two chromatics, when, by the elevation of one and depression of the other, they are united into one.
  4. Randel, Don Michael, ed. (2003). "Set theory". The Harvard Dictionary of Music (4th ed.). Cambridge, MA: Belknap Press of Harvard University Press. p. 776. ISBN 978-0-674-01163-2.
  5. Randel, Don Michael, ed. (2003). "Enharmonic". The Harvard Dictionary of Music (4th ed.). Cambridge, MA: Belknap Press of Harvard University Press. p. 295. ISBN 978-0-674-01163-2.
  6. Kern, J. and Hammerstein, O. (1939, bars 23-25) “All the things you are”, New York, T. B. Harms Co.
  7. https://www.youtube.com/watch?v=OPapxr8GvGA
  8. Mellers, W. (1983, p.132) Beethoven and the Voice of God. London, Faber.
  9. Walker, A. (2018, p. 383), Fryderyk Chopin, a Life and Times. London, Faber.
  10. David Allen (1 August 2016). "Schubert's Final Acceptance, Rueful as Always". The New York Times. Retrieved 10 August 2020.
  11. Rushton, Julian (2001). "Enharmonic". In Sadie, Stanley; Tyrrell, John (eds.). The New Grove Dictionary of Music and Musicians (2nd ed.). London: Macmillan Publishers. ISBN 0-19-517067-9.
  12. Barbera, C. André (1977). "Arithmetic and Geometric Divisions of the Tetrachord". Journal of Music Theory. 21 (2): 294–323.

Further reading
  • The dictionary definition of enharmonic at Wiktionary
  • Media related to Enharmonic at Wikimedia Commons
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.