Electron configuration
In atomic physics and quantum chemistry, the electron configuration is the distribution of electrons of an atom or molecule (or other physical structure) in atomic or molecular orbitals.[1] For example, the electron configuration of the neon atom is 1s2 2s2 2p6, using the notation explained below.

Electronic configurations describe each electron as moving independently in an orbital, in an average field created by all other orbitals. Mathematically, configurations are described by Slater determinants or configuration state functions.
According to the laws of quantum mechanics, for systems with only one electron, a level of energy is associated with each electron configuration and in certain conditions, electrons are able to move from one configuration to another by the emission or absorption of a quantum of energy, in the form of a photon.
Knowledge of the electron configuration of different atoms is useful in understanding the structure of the periodic table of elements. This is also useful for describing the chemical bonds that hold atoms together. In bulk materials, this same idea helps explain the peculiar properties of lasers and semiconductors.
Shells and subshells
| s (ℓ=0) | p (ℓ=1) | |||
|---|---|---|---|---|
| m=0 | m=0 | m=±1 | ||
| s | pz | px | py | |
| n=1 | ||||
| n=2 | ||||
Electron configuration was first conceived under the Bohr model of the atom, and it is still common to speak of shells and subshells despite the advances in understanding of the quantum-mechanical nature of electrons.
An electron shell is the set of allowed states that share the same principal quantum number, n (the number before the letter in the orbital label), that electrons may occupy. An atom's nth electron shell can accommodate 2n2 electrons, e.g. the first shell can accommodate 2 electrons, the second shell 8 electrons, the third shell 18 electrons and so on. The factor of two arises because the allowed states are doubled due to electron spin—each atomic orbital admits up to two otherwise identical electrons with opposite spin, one with a spin +1/2 (usually denoted by an up-arrow) and one with a spin −1/2 (with a down-arrow).
A subshell is the set of states defined by a common azimuthal quantum number, ℓ, within a shell. The values ℓ = 0, 1, 2, 3 correspond to the s, p, d, and f labels, respectively. For example, the 3d subshell has n = 3 and ℓ = 2. The maximum number of electrons that can be placed in a subshell is given by 2(2ℓ+1). This gives two electrons in an s subshell, six electrons in a p subshell, ten electrons in a d subshell and fourteen electrons in an f subshell.
The numbers of electrons that can occupy each shell and each subshell arise from the equations of quantum mechanics,[2] in particular the Pauli exclusion principle, which states that no two electrons in the same atom can have the same values of the four quantum numbers.[3]
Open and closed shells
In the context of atomic orbitals, an open shell is a valence shell which is not completely filled with electrons or that has not given all of its valence electrons through chemical bonds with other atoms or molecules during a chemical reaction. Atoms generally reach a noble gas configuration in a molecule. The noble gases (He, Ne, Ar, Kr, Xe, Rn) are less reactive and have configurations 1s2 (He), 1s22s22p6 (Ne), 1s22s22p63s23p6 (Ar), etc.
For molecules it signifies that there are unpaired electrons. In molecular orbital theory, this leads to molecular orbitals that are singly occupied. In computational chemistry implementations of molecular orbital theory, open shell molecules have to be handled by either the restricted open-shell Hartree–Fock method or the unrestricted Hartree–Fock method.
Likewise a closed shell or closed shell configuration is obtained with a completely filled valence shell. This configuration is very stable.[4] In another meaning a closed shell configuration corresponds to a state where all molecular orbitals are either doubly occupied or empty (a singlet state).[5] Open shell molecules are more difficult to study computationally[6]
Notation
Physicists and chemists use a standard notation to indicate the electron configurations of atoms and molecules. For atoms, the notation consists of a sequence of atomic subshell labels (e.g. for phosphorus the sequence 1s, 2s, 2p, 3s, 3p) with the number of electrons assigned to each subshell placed as a superscript. For example, hydrogen has one electron in the s-orbital of the first shell, so its configuration is written 1s1. Lithium has two electrons in the 1s-subshell and one in the (higher-energy) 2s-subshell, so its configuration is written 1s2 2s1 (pronounced "one-s-two, two-s-one"). Phosphorus (atomic number 15) is as follows: 1s2 2s2 2p6 3s2 3p3.
For atoms with many electrons, this notation can become lengthy and so an abbreviated notation is used. The electron configuration can be visualized as the core electrons, equivalent to the noble gas of the preceding period, and the valence electrons: each element in a period differs only by the last few subshells. Phosphorus, for instance, is in the third period. It differs from the second-period neon, whose configuration is 1s2 2s2 2p6, only by the presence of a third shell. The portion of its configuration that is equivalent to neon is abbreviated as [Ne], allowing the configuration of phosphorus to be written as [Ne] 3s2 3p3 rather than writing out the details of the configuration of neon explicitly. This convention is useful as it is the electrons in the outermost shell that most determine the chemistry of the element.
For a given configuration, the order of writing the orbitals is not completely fixed since only the orbital occupancies have physical significance. For example, the electron configuration of the titanium ground state can be written as either [Ar] 4s2 3d2 or [Ar] 3d2 4s2. The first notation follows the order based on the Madelung rule for the configurations of neutral atoms; 4s is filled before 3d in the sequence Ar, K, Ca, Sc, Ti. The second notation groups all orbitals with the same value of n together, corresponding to the "spectroscopic" order of orbital energies that is the reverse of the order in which electrons are removed from a given atom to form positive ions; 3d is filled before 4s in the sequence Ti4+, Ti3+, Ti2+, Ti+, Ti.
The superscript 1 for a singly occupied subshell is not compulsory; for example aluminium may be written as either [Ne] 3s2 3p1 or [Ne] 3s2 3p. It is quite common to see the letters of the orbital labels (s, p, d, f) written in an italic or slanting typeface, although the International Union of Pure and Applied Chemistry (IUPAC) recommends a normal typeface (as used here). The choice of letters originates from a now-obsolete system of categorizing spectral lines as "sharp", "principal", "diffuse" and "fundamental" (or "fine"), based on their observed fine structure: their modern usage indicates orbitals with an azimuthal quantum number, l, of 0, 1, 2 or 3 respectively. After "f", the sequence continues alphabetically "g", "h", "i"... (l = 4, 5, 6...), skipping "j", although orbitals of these types are rarely required.[7][8]
The electron configurations of molecules are written in a similar way, except that molecular orbital labels are used instead of atomic orbital labels (see below).
Energy—ground state and excited states
The energy associated to an electron is that of its orbital. The energy of a configuration is often approximated as the sum of the energy of each electron, neglecting the electron-electron interactions. The configuration that corresponds to the lowest electronic energy is called the ground state. Any other configuration is an excited state.
As an example, the ground state configuration of the sodium atom is 1s2 2s2 2p6 3s1, as deduced from the Aufbau principle (see below). The first excited state is obtained by promoting a 3s electron to the 3p orbital, to obtain the 1s2 2s2 2p6 3p1 configuration, abbreviated as the 3p level. Atoms can move from one configuration to another by absorbing or emitting energy. In a sodium-vapor lamp for example, sodium atoms are excited to the 3p level by an electrical discharge, and return to the ground state by emitting yellow light of wavelength 589 nm.
Usually, the excitation of valence electrons (such as 3s for sodium) involves energies corresponding to photons of visible or ultraviolet light. The excitation of core electrons is possible, but requires much higher energies, generally corresponding to x-ray photons. This would be the case for example to excite a 2p electron of sodium to the 3s level and form the excited 1s2 2s2 2p5 3s2 configuration.
The remainder of this article deals only with the ground-state configuration, often referred to as "the" configuration of an atom or molecule.
History
Irving Langmuir was the first to propose in his 1919 article "The Arrangement of Electrons in Atoms and Molecules" in which, building on Gilbert N. Lewis's cubical atom theory and Walther Kossel's chemical bonding theory, he outlined his "concentric theory of atomic structure".[9] Langmuir had developed his work on electron atomic structure from other chemists as is shown in the development of the History of the periodic table and the Octet rule. Niels Bohr (1923) incorporated Langmuir’s model that the periodicity in the properties of the elements might be explained by the electronic structure of the atom.[10] His proposals were based on the then current Bohr model of the atom, in which the electron shells were orbits at a fixed distance from the nucleus. Bohr's original configurations would seem strange to a present-day chemist: sulfur was given as 2.4.4.6 instead of 1s2 2s2 2p6 3s2 3p4 (2.8.6). Bohr used 4 and 6 following Alfred Werner‘s 1893 paper. In fact, the chemists believed in atoms long before the physicists. Langmuir began his paper referenced above by saying, “The problem of the structure of atoms has been attacked mainly by physicists who have given little consideration to the chemical properties which must ultimately be explained by a theory of atomic structure. The vast store of knowledge of chemical properties and relationships, such as is summarized by the Periodic Table, should serve as a better foundation for a theory of atomic structure than the relatively meager experimental data along purely physical lines... These electrons arrange themselves in a series of concentric shells, the first shell containing two electrons, while all other shells tend to hold eight.” The valence electrons in the atom were described by Richard Abegg in 1904.[11]
In 1924, E. C. Stoner incorporated Sommerfeld's third quantum number into the description of electron shells, and correctly predicted the shell structure of sulfur to be 2.8.6.[12] However neither Bohr's system nor Stoner's could correctly describe the changes in atomic spectra in a magnetic field (the Zeeman effect).
Bohr was well aware of this shortcoming (and others), and had written to his friend Wolfgang Pauli to ask for his help in saving quantum theory (the system now known as "old quantum theory"). Pauli realized that the Zeeman effect must be due only to the outermost electrons of the atom, and was able to reproduce Stoner's shell structure, but with the correct structure of subshells, by his inclusion of a fourth quantum number and his exclusion principle (1925):[13]
It should be forbidden for more than one electron with the same value of the main quantum number n to have the same value for the other three quantum numbers k [l], j [ml] and m [ms].
The Schrödinger equation, published in 1926, gave three of the four quantum numbers as a direct consequence of its solution for the hydrogen atom:[2] this solution yields the atomic orbitals that are shown today in textbooks of chemistry (and above). The examination of atomic spectra allowed the electron configurations of atoms to be determined experimentally, and led to an empirical rule (known as Madelung's rule (1936),[14] see below) for the order in which atomic orbitals are filled with electrons.
Atoms: Aufbau principle and Madelung rule
The aufbau principle (from the German Aufbau, "building up, construction") was an important part of Bohr's original concept of electron configuration. It may be stated as:[15]
- a maximum of two electrons are put into orbitals in the order of increasing orbital energy: the lowest-energy orbitals are filled before electrons are placed in higher-energy orbitals.
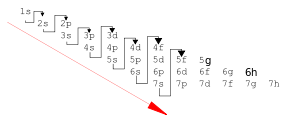
The principle works very well (for the ground states of the atoms) for the first 18 elements, then decreasingly well for the following 100 elements. The modern form of the aufbau principle describes an order of orbital energies given by Madelung's rule (or Klechkowski's rule). This rule was first stated by Charles Janet in 1929, rediscovered by Erwin Madelung in 1936,[14] and later given a theoretical justification by V.M. Klechkowski:[16]
- Orbitals are filled in the order of increasing n+l;
- Where two orbitals have the same value of n+l, they are filled in order of increasing n.
This gives the following order for filling the orbitals:
- 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p, (8s, 5g, 6f, 7d, 8p, and 9s)
In this list the orbitals in parentheses are not occupied in the ground state of the heaviest atom now known (Og, Z = 118).
The aufbau principle can be applied, in a modified form, to the protons and neutrons in the atomic nucleus, as in the shell model of nuclear physics and nuclear chemistry.
Periodic table
.svg.png)
Note that although the Madelung rule predicts that 4f should fill before 5d, this table follows most chemistry texts and breaks the d block apart, filling one 5d electron before the 4f electrons are supposed to go in. It is known that the 4f orbitals actually already become non-hydrogenic and rare-earth-like at lanthanum rather than cerium, and some authors have on this and other bases advocated drawing a table following Madelung's rule more closely and not having this gap.[17] However the traditional form with a broken d-block still appears in a plurality of textbooks published in the 2010s, and most chemists seem either unconvinced by or unaware of the arguments to change it;[18] as such the traditional form has been shown above.
The form of the periodic table is closely related to the electron configuration of the atoms of the elements. For example, all the elements of group 2 have an electron configuration of [E] ns2 (where [E] is an inert gas configuration), and have notable similarities in their chemical properties. In general, the periodicity of the periodic table in terms of periodic table blocks is clearly due to the number of electrons (2, 6, 10, 14...) needed to fill s, p, d, and f subshells.
The outermost electron shell is often referred to as the "valence shell" and (to a first approximation) determines the chemical properties. It should be remembered that the similarities in the chemical properties were remarked on more than a century before the idea of electron configuration.[19] It is not clear how far Madelung's rule explains (rather than simply describes) the periodic table,[20] although some properties (such as the common +2 oxidation state in the first row of the transition metals) would obviously be different with a different order of orbital filling.
Shortcomings of the aufbau principle
The aufbau principle rests on a fundamental postulate that the order of orbital energies is fixed, both for a given element and between different elements; in both cases this is only approximately true. It considers atomic orbitals as "boxes" of fixed energy into which can be placed two electrons and no more. However, the energy of an electron "in" an atomic orbital depends on the energies of all the other electrons of the atom (or ion, or molecule, etc.). There are no "one-electron solutions" for systems of more than one electron, only a set of many-electron solutions that cannot be calculated exactly[21] (although there are mathematical approximations available, such as the Hartree–Fock method).
The fact that the aufbau principle is based on an approximation can be seen from the fact that there is an almost-fixed filling order at all, that, within a given shell, the s-orbital is always filled before the p-orbitals. In a hydrogen-like atom, which only has one electron, the s-orbital and the p-orbitals of the same shell have exactly the same energy, to a very good approximation in the absence of external electromagnetic fields. (However, in a real hydrogen atom, the energy levels are slightly split by the magnetic field of the nucleus, and by the quantum electrodynamic effects of the Lamb shift.)
Ionization of the transition metals
The naïve application of the aufbau principle leads to a well-known paradox (or apparent paradox) in the basic chemistry of the transition metals. Potassium and calcium appear in the periodic table before the transition metals, and have electron configurations [Ar] 4s1 and [Ar] 4s2 respectively, i.e. the 4s-orbital is filled before the 3d-orbital. This is in line with Madelung's rule, as the 4s-orbital has n+l = 4 (n = 4, l = 0) while the 3d-orbital has n+l = 5 (n = 3, l = 2). After calcium, most neutral atoms in the first series of transition metals (Sc-Zn) have configurations with two 4s electrons, but there are two exceptions. Chromium and copper have electron configurations [Ar] 3d5 4s1 and [Ar] 3d10 4s1 respectively, i.e. one electron has passed from the 4s-orbital to a 3d-orbital to generate a half-filled or filled subshell. In this case, the usual explanation is that "half-filled or completely filled subshells are particularly stable arrangements of electrons". However this is not supported by the facts, as tungsten (W) has a Madelung-following d4s2 configuration and not d5s1, and niobium (Nb) has an anomalous d4s1 configuration that does not give it a half-filled or completely filled subshell.[22]
The apparent paradox arises when electrons are removed from the transition metal atoms to form ions. The first electrons to be ionized come not from the 3d-orbital, as one would expect if it were "higher in energy", but from the 4s-orbital. This interchange of electrons between 4s and 3d is found for all atoms of the first series of transition metals.[23] The configurations of the neutral atoms (K, Ca, Sc, Ti, V, Cr, ...) usually follow the order 1s, 2s, 2p, 3s, 3p, 4s, 3d, ...; however the successive stages of ionization of a given atom (such as Fe4+, Fe3+, Fe2+, Fe+, Fe) usually follow the order 1s, 2s, 2p, 3s, 3p, 3d, 4s, ...
This phenomenon is only paradoxical if it is assumed that the energy order of atomic orbitals is fixed and unaffected by the nuclear charge or by the presence of electrons in other orbitals. If that were the case, the 3d-orbital would have the same energy as the 3p-orbital, as it does in hydrogen, yet it clearly doesn't. There is no special reason why the Fe2+ ion should have the same electron configuration as the chromium atom, given that iron has two more protons in its nucleus than chromium, and that the chemistry of the two species is very different. Melrose and Eric Scerri have analyzed the changes of orbital energy with orbital occupations in terms of the two-electron repulsion integrals of the Hartree-Fock method of atomic structure calculation.[24] More recently Scerri has argued that contrary to what is stated in the vast majority of sources including the title of his previous article on the subject, 3d orbitals rather than 4s are in fact preferentially occupied.[25]
In chemical environments, configurations can change even more: Th3+ as a bare ion has a configuration of [Rn]5f1, yet in most ThIII compounds the thorium atom has a 6d1 configuration instead.[26][27] Mostly, what is present is rather a superposition of various configurations.[22] For instance, copper metal is not well-described by either an [Ar]3d104s1 or an [Ar]3d94s2 configuration, but is rather well described as a 90% contribution of the first and a 10% contribution of the second. Indeed, visible light is already enough to excite electrons in most transition metals, and they often continuously "flow" through different configurations when that happens (copper and its group are an exception).[28]
Similar ion-like 3dx4s0 configurations occur in transition metal complexes as described by the simple crystal field theory, even if the metal has oxidation state 0. For example, chromium hexacarbonyl can be described as a chromium atom (not ion) surrounded by six carbon monoxide ligands. The electron configuration of the central chromium atom is described as 3d6 with the six electrons filling the three lower-energy d orbitals between the ligands. The other two d orbitals are at higher energy due to the crystal field of the ligands. This picture is consistent with the experimental fact that the complex is diamagnetic, meaning that it has no unpaired electrons. However, in a more accurate description using molecular orbital theory, the d-like orbitals occupied by the six electrons are no longer identical with the d orbitals of the free atom.
Other exceptions to Madelung's rule
There are several more exceptions to Madelung's rule among the heavier elements, and as atomic number increases it becomes more and more difficult to find simple explanations such as the stability of half-filled subshells. It is possible to predict most of the exceptions by Hartree–Fock calculations,[29] which are an approximate method for taking account of the effect of the other electrons on orbital energies. Qualitatively, for example, we can see that the 4d elements have the greatest concentration of Madelung anomalies, because the 4d–5s gap is smaller than the 3d–4s and 5d–6s gaps.[30]
For the heavier elements, it is also necessary to take account of the effects of special relativity on the energies of the atomic orbitals, as the inner-shell electrons are moving at speeds approaching the speed of light. In general, these relativistic effects[31] tend to decrease the energy of the s-orbitals in relation to the other atomic orbitals.[32] This is the reason why the 6d elements are predicted to have no Madelung anomalies apart from lawrencium (for which relativistic effects stabilise the p1/2 orbital as well and cause its occupancy in the ground state), as relativity intervenes to make the 7s orbitals lower in energy than the 6d ones.
The table below shows the ground state configuration in terms of orbital occupancy, but it does not show the ground state in terms of the sequence of orbital energies as determined spectroscopically. For example, in the transition metals, the 4s orbital is of a higher energy than the 3d orbitals; and in the lanthanides, the 6s is higher than the 4f and 5d. The ground states can be seen in the Electron configurations of the elements (data page). However this also depends on the charge: a Ca atom has 4s lower in energy than 3d, but a Ca2+ cation has 3d lower in energy than 4s. In practice the configurations predicted by the Madelung rule are at least close to the ground state even in these anomalous cases.[33] The empty f orbitals in lanthanum, actinium, and thorium contribute to chemical bonding,[34][35] as do the empty p orbitals in transition metals.[36]
Vacant s, d, and f orbitals have been shown explicitly, as is occasionally done,[37] to emphasise the filling order and to clarify that even orbitals unoccupied in the ground state (e.g. lanthanum 4f or palladium 5s) may be occupied and bonding in chemical compounds. (The same is also true for the p-orbitals, which are not explicitly shown because they are only actually occupied for lawrencium in gas-phase ground states.)
| Period 4 | Period 5 | Period 6 | Period 7 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Element | Z | Electron Configuration | Element | Z | Electron Configuration | Element | Z | Electron Configuration | Element | Z | Electron Configuration | |||
| Lanthanum | 57 | [Xe] 6s2 4f0 5d1 | Actinium | 89 | [Rn] 7s2 5f0 6d1 | |||||||||
| Cerium | 58 | [Xe] 6s2 4f1 5d1 | Thorium | 90 | [Rn] 7s2 5f0 6d2 | |||||||||
| Praseodymium | 59 | [Xe] 6s2 4f3 5d0 | Protactinium | 91 | [Rn] 7s2 5f2 6d1 | |||||||||
| Neodymium | 60 | [Xe] 6s2 4f4 5d0 | Uranium | 92 | [Rn] 7s2 5f3 6d1 | |||||||||
| Promethium | 61 | [Xe] 6s2 4f5 5d0 | Neptunium | 93 | [Rn] 7s2 5f4 6d1 | |||||||||
| Samarium | 62 | [Xe] 6s2 4f6 5d0 | Plutonium | 94 | [Rn] 7s2 5f6 6d0 | |||||||||
| Europium | 63 | [Xe] 6s2 4f7 5d0 | Americium | 95 | [Rn] 7s2 5f7 6d0 | |||||||||
| Gadolinium | 64 | [Xe] 6s2 4f7 5d1 | Curium | 96 | [Rn] 7s2 5f7 6d1 | |||||||||
| Terbium | 65 | [Xe] 6s2 4f9 5d0 | Berkelium | 97 | [Rn] 7s2 5f9 6d0 | |||||||||
| Dysprosium | 66 | [Xe] 6s2 4f10 5d0 | Californium | 98 | [Rn] 7s2 5f10 6d0 | |||||||||
| Holmium | 67 | [Xe] 6s2 4f11 5d0 | Einsteinium | 99 | [Rn] 7s2 5f11 6d0 | |||||||||
| Erbium | 68 | [Xe] 6s2 4f12 5d0 | Fermium | 100 | [Rn] 7s2 5f12 6d0 | |||||||||
| Thulium | 69 | [Xe] 6s2 4f13 5d0 | Mendelevium | 101 | [Rn] 7s2 5f13 6d0 | |||||||||
| Ytterbium | 70 | [Xe] 6s2 4f14 5d0 | Nobelium | 102 | [Rn] 7s2 5f14 6d0 | |||||||||
| Scandium | 21 | [Ar] 4s2 3d1 | Yttrium | 39 | [Kr] 5s2 4d1 | Lutetium | 71 | [Xe] 6s2 4f14 5d1 | Lawrencium | 103 | [Rn] 7s2 5f14 6d0 7p1 | |||
| Titanium | 22 | [Ar] 4s2 3d2 | Zirconium | 40 | [Kr] 5s2 4d2 | Hafnium | 72 | [Xe] 6s2 4f14 5d2 | Rutherfordium | 104 | [Rn] 7s2 5f14 6d2 | |||
| Vanadium | 23 | [Ar] 4s2 3d3 | Niobium | 41 | [Kr] 5s1 4d4 | Tantalum | 73 | [Xe] 6s2 4f14 5d3 | Dubnium | 105 | [Rn] 7s2 5f14 6d3 | |||
| Chromium | 24 | [Ar] 4s1 3d5 | Molybdenum | 42 | [Kr] 5s1 4d5 | Tungsten | 74 | [Xe] 6s2 4f14 5d4 | Seaborgium | 106 | [Rn] 7s2 5f14 6d4 | |||
| Manganese | 25 | [Ar] 4s2 3d5 | Technetium | 43 | [Kr] 5s2 4d5 | Rhenium | 75 | [Xe] 6s2 4f14 5d5 | Bohrium | 107 | [Rn] 7s2 5f14 6d5 | |||
| Iron | 26 | [Ar] 4s2 3d6 | Ruthenium | 44 | [Kr] 5s1 4d7 | Osmium | 76 | [Xe] 6s2 4f14 5d6 | Hassium | 108 | [Rn] 7s2 5f14 6d6 | |||
| Cobalt | 27 | [Ar] 4s2 3d7 | Rhodium | 45 | [Kr] 5s1 4d8 | Iridium | 77 | [Xe] 6s2 4f14 5d7 | Meitnerium | 109 | [Rn] 7s2 5f14 6d7 (predicted) | |||
| Nickel | 28 | [Ar] 4s2 3d8 or [Ar] 4s1 3d9 (disputed)[39] | Palladium | 46 | [Kr] 5s0 4d10 | Platinum | 78 | [Xe] 6s1 4f14 5d9 | Darmstadtium | 110 | [Rn] 7s2 5f14 6d8 (predicted) | |||
| Copper | 29 | [Ar] 4s1 3d10 | Silver | 47 | [Kr] 5s1 4d10 | Gold | 79 | [Xe] 6s1 4f14 5d10 | Roentgenium | 111 | [Rn] 7s2 5f14 6d9 (predicted) | |||
| Zinc | 30 | [Ar] 4s2 3d10 | Cadmium | 48 | [Kr] 5s2 4d10 | Mercury | 80 | [Xe] 6s2 4f14 5d10 | Copernicium | 112 | [Rn] 7s2 5f14 6d10 (predicted) | |||
The electron-shell configuration of elements beyond hassium has not yet been empirically verified, but they are expected to follow Madelung's rule without exceptions until element 120. Beyond element 120, Madelung's rule is expected to stop holding altogether due to the closeness in energy of the 5g, 6f, 7d, and 8p1/2 orbitals.[40]
Electron configuration in molecules
In molecules, the situation becomes more complex, as each molecule has a different orbital structure. The molecular orbitals are labelled according to their symmetry,[41] rather than the atomic orbital labels used for atoms and monatomic ions: hence, the electron configuration of the dioxygen molecule, O2, is written 1σg2 1σu2 2σg2 2σu2 3σg2 1πu4 1πg2,[42][43] or equivalently 1σg2 1σu2 2σg2 2σu2 1πu4 3σg2 1πg2.[1] The term 1πg2 represents the two electrons in the two degenerate π*-orbitals (antibonding). From Hund's rules, these electrons have parallel spins in the ground state, and so dioxygen has a net magnetic moment (it is paramagnetic). The explanation of the paramagnetism of dioxygen was a major success for molecular orbital theory.
The electronic configuration of polyatomic molecules can change without absorption or emission of a photon through vibronic couplings.
Electron configuration in solids
In a solid, the electron states become very numerous. They cease to be discrete, and effectively blend into continuous ranges of possible states (an electron band). The notion of electron configuration ceases to be relevant, and yields to band theory.
Applications
The most widespread application of electron configurations is in the rationalization of chemical properties, in both inorganic and organic chemistry. In effect, electron configurations, along with some simplified form of molecular orbital theory, have become the modern equivalent of the valence concept, describing the number and type of chemical bonds that an atom can be expected to form.
This approach is taken further in computational chemistry, which typically attempts to make quantitative estimates of chemical properties. For many years, most such calculations relied upon the "linear combination of atomic orbitals" (LCAO) approximation, using an ever-larger and more complex basis set of atomic orbitals as the starting point. The last step in such a calculation is the assignment of electrons among the molecular orbitals according to the Aufbau principle. Not all methods in calculational chemistry rely on electron configuration: density functional theory (DFT) is an important example of a method that discards the model.
For atoms or molecules with more than one electron, the motion of electrons are correlated and such a picture is no longer exact. A very large number of electronic configurations are needed to exactly describe any multi-electron system, and no energy can be associated with one single configuration. However, the electronic wave function is usually dominated by a very small number of configurations and therefore the notion of electronic configuration remains essential for multi-electron systems.
A fundamental application of electron configurations is in the interpretation of atomic spectra. In this case, it is necessary to supplement the electron configuration with one or more term symbols, which describe the different energy levels available to an atom. Term symbols can be calculated for any electron configuration, not just the ground-state configuration listed in tables, although not all the energy levels are observed in practice. It is through the analysis of atomic spectra that the ground-state electron configurations of the elements were experimentally determined.
See also
- Born–Oppenheimer approximation
- Electron configurations of the elements (data page)
- Periodic table (electron configurations)
- Molecular term symbol
- HOMO/LUMO
- Group (periodic table)
- d electron count
- Extended periodic table – discusses the limits of the periodic table
- Spherical harmonics
- Free radical
- Octet rule
- Valence shell
Notes
- IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "configuration (electronic)". doi:10.1351/goldbook.C01248
- In formal terms, the quantum numbers n, ℓ and mℓ arise from the fact that the solutions to the time-independent Schrödinger equation for hydrogen-like atoms are based on spherical harmonics.
- IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Pauli exclusion principle". doi:10.1351/goldbook.PT07089
- "Periodic table". Archived from the original on 3 November 2007. Retrieved 1 November 2007.
- "Chapter 11. Configuration Interaction". www.semichem.com.
- "Laboratory for Theoretical Studies of Electronic Structure and Spectroscopy of Open-Shell and Electronically Excited Species - iOpenShell". iopenshell.usc.edu.
- Weisstein, Eric W. (2007). "Electron Orbital". wolfram.
- Ebbing, Darrell D.; Gammon, Steven D. (12 January 2007). General Chemistry. p. 284. ISBN 978-0-618-73879-3.
- Langmuir, Irving (June 1919). "The Arrangement of Electrons in Atoms and Molecules". Journal of the American Chemical Society. 41 (6): 868–934. doi:10.1021/ja02227a002.
- Bohr, Niels (1923). "Über die Anwendung der Quantumtheorie auf den Atombau. I". Zeitschrift für Physik. 13 (1): 117. Bibcode:1923ZPhy...13..117B. doi:10.1007/BF01328209. S2CID 123582460.
- Abegg, R. (1904). "Die Valenz und das periodische System. Versuch einer Theorie der Molekularverbindungen" [Valency and the periodic system. Attempt at a theory of molecular compounds]. Zeitschrift für Anorganische Chemie. 39 (1): 330–380. doi:10.1002/zaac.19040390125.
- Stoner, E.C. (1924). "The distribution of electrons among atomic levels". Philosophical Magazine. 6th Series. 48 (286): 719–36. doi:10.1080/14786442408634535.
- Pauli, Wolfgang (1925). "Über den Einfluss der Geschwindigkeitsabhändigkeit der elektronmasse auf den Zeemaneffekt". Zeitschrift für Physik. 31 (1): 373. Bibcode:1925ZPhy...31..373P. doi:10.1007/BF02980592. S2CID 122477612. English translation from Scerri, Eric R. (1991). "The Electron Configuration Model, Quantum Mechanics and Reduction" (PDF). The British Journal for the Philosophy of Science. 42 (3): 309–25. doi:10.1093/bjps/42.3.309.
- Madelung, Erwin (1936). Mathematische Hilfsmittel des Physikers. Berlin: Springer.
- IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "aufbau principle". doi:10.1351/goldbook.AT06996
- Wong, D. Pan (1979). "Theoretical justification of Madelung's rule". Journal of Chemical Education. 56 (11): 714–18. Bibcode:1979JChEd..56..714W. doi:10.1021/ed056p714.
- Hamilton, David C. (1965). "Position of Lanthanum in the Periodic Table". American Journal of Physics. 33 (8): 637–640. doi:10.1119/1.1972042.
- Scerri, E. (2012). "Mendeleev's Periodic Table Is Finally Completed and What To Do about Group 3?". Chemistry International. 34 (4). doi:10.1515/ci.2012.34.4.28. Archived from the original on 5 July 2017.
- The similarities in chemical properties and the numerical relationship between the atomic weights of calcium, strontium and barium was first noted by Johann Wolfgang Döbereiner in 1817.
- Scerri, Eric R. (1998). "How Good Is the Quantum Mechanical Explanation of the Periodic System?" (PDF). Journal of Chemical Education. 75 (11): 1384–85. Bibcode:1998JChEd..75.1384S. doi:10.1021/ed075p1384. Ostrovsky, V.N. (2005). "On Recent Discussion Concerning Quantum Justification of the Periodic Table of the Elements". Foundations of Chemistry. 7 (3): 235–39. doi:10.1007/s10698-005-2141-y. S2CID 93589189.
- Electrons are identical particles, a fact that is sometimes referred to as "indistinguishability of electrons". A one-electron solution to a many-electron system would imply that the electrons could be distinguished from one another, and there is strong experimental evidence that they can't be. The exact solution of a many-electron system is a n-body problem with n ≥ 3 (the nucleus counts as one of the "bodies"): such problems have evaded analytical solution since at least the time of Euler.
- Scerri, Eric (2019). "Five ideas in chemical education that must die". Foundations of Chemistry. 21: 61–69. doi:10.1007/s10698-018-09327-y.
- There are some cases in the second and third series where the electron remains in an s-orbital.
- Melrose, Melvyn P.; Scerri, Eric R. (1996). "Why the 4s Orbital is Occupied before the 3d". Journal of Chemical Education. 73 (6): 498–503. Bibcode:1996JChEd..73..498M. doi:10.1021/ed073p498.
- Scerri, Eric (7 November 2013). "The trouble with the aufbau principle". Education in Chemistry. Vol. 50 no. 6. Royal Society of Chemistry. pp. 24–26. Archived from the original on 21 January 2018. Retrieved 12 June 2018.
- Langeslay, Ryan R.; Fieser, Megan E.; Ziller, Joseph W.; Furche, Philip; Evans, William J. (2015). "Synthesis, structure, and reactivity of crystalline molecular complexes of the {[C5H3(SiMe3)2]3Th}1− anion containing thorium in the formal +2 oxidation state". Chem. Sci. 6 (1): 517–521. doi:10.1039/C4SC03033H. PMC 5811171. PMID 29560172.
- Wickleder, Mathias S.; Fourest, Blandine; Dorhout, Peter K. (2006). "Thorium". In Morss, Lester R.; Edelstein, Norman M.; Fuger, Jean (eds.). The Chemistry of the Actinide and Transactinide Elements (PDF). 3 (3rd ed.). Dordrecht, the Netherlands: Springer. pp. 52–160. doi:10.1007/1-4020-3598-5_3. Archived from the original (PDF) on 7 March 2016.
- 10.26434/chemrxiv.11860941
- Meek, Terry L.; Allen, Leland C. (2002). "Configuration irregularities: deviations from the Madelung rule and inversion of orbital energy levels". Chemical Physics Letters. 362 (5–6): 362–64. Bibcode:2002CPL...362..362M. doi:10.1016/S0009-2614(02)00919-3.
- Kulsha, Andrey (2004). "Периодическая система химических элементов Д. И. Менделеева" [D. I. Mendeleev's periodic system of the chemical elements] (PDF). primefan.ru (in Russian). Retrieved 17 May 2020.
- IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "relativistic effects". doi:10.1351/goldbook.RT07093
- Pyykkö, Pekka (1988). "Relativistic effects in structural chemistry". Chemical Reviews. 88 (3): 563–94. doi:10.1021/cr00085a006.
- See the NIST tables
- Glotzel, D. (1978). "Ground-state properties of f band metals: lanthanum, cerium and thorium". Journal of Physics F: Metal Physics. 8 (7): L163–L168. Bibcode:1978JPhF....8L.163G. doi:10.1088/0305-4608/8/7/004.
- Xu, Wei; Ji, Wen-Xin; Qiu, Yi-Xiang; Schwarz, W. H. Eugen; Wang, Shu-Guang (2013). "On structure and bonding of lanthanoid trifluorides LnF3 (Ln = La to Lu)". Physical Chemistry Chemical Physics. 2013 (15): 7839–47. Bibcode:2013PCCP...15.7839X. doi:10.1039/C3CP50717C. PMID 23598823.
- Example for platinum
- See for example this Russian periodic table poster by A. V. Kulsha and T. A. Kolevich
- Miessler, G. L.; Tarr, D. A. (1999). Inorganic Chemistry (2nd ed.). Prentice-Hall. p. 38.
- Scerri, Eric R. (2007). The periodic table: its story and its significance. Oxford University Press. pp. 239–240. ISBN 978-0-19-530573-9.
- Hoffman, Darleane C.; Lee, Diana M.; Pershina, Valeria (2006). "Transactinides and the future elements". In Morss; Edelstein, Norman M.; Fuger, Jean (eds.). The Chemistry of the Actinide and Transactinide Elements (3rd ed.). Dordrecht, The Netherlands: Springer Science+Business Media. ISBN 978-1-4020-3555-5.
- The labels are written in lowercase to indicate that they correspond to one-electron functions. They are numbered consecutively for each symmetry type (irreducible representation in the character table of the point group for the molecule), starting from the orbital of lowest energy for that type.
- Levine I.N. Quantum Chemistry (4th ed., Prentice Hall 1991) p.376 ISBN 0-205-12770-3
- Miessler G.L. and Tarr D.A. Inorganic Chemistry (2nd ed., Prentice Hall 1999) p.118 ISBN 0-13-841891-8
External links
| Wikimedia Commons has media related to Electron configurations. |
