Eight-bar linkage

An eight-bar linkage is a one degree-of-freedom mechanism that is constructed from eight links and 10 joints.[1] These linkages are rare compared to four-bar and six-bar linkages, but two well-known examples are the Peaucellier linkage and the linkage designed by Theo Jansen for his walking machines.

Peaucellier-Lipkin linkage:
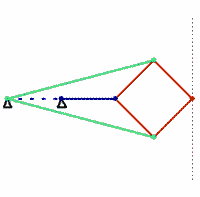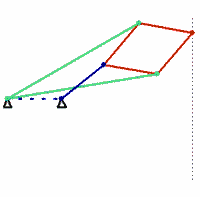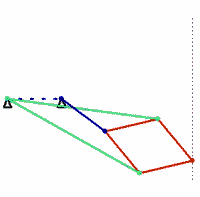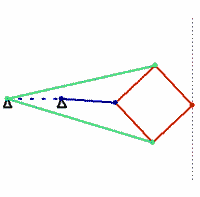
bars of identical colour are of equal length
Theo Jansen's kinetic sculpture Strandbeest. A wind-driven walking machine.

Classification of eight-bar linkages

Eight-bar linkages are classified by how many binary, ternary and quaternary links they have. A binary link connects two joints, a ternary link connects three joints and a quaternary link connects four joints. There are three classes of eight-bar linkage denoted (4, 4, 0, 0), (5, 2, 1, 0) and (6, 0, 2, 0), distinguished by the count of binary, ternary and quaternary links, when read from left to right---the final zero is traditionally added to the class label though no eight-bar linkage has a quintanary link..[2]

There are sixteen different topologies of eight-bar linkages which are distinguished by their non-isomorphic linkage graphs. Of these 16 topologies, nine are in class (4, 4, 0, 0), five are in (5, 2, 1, 0) and two in (6, 0, 2, 0).

The Peaucellier linkage

The Peaucellier linkage (or Peaucellier–Lipkin cell, or Peaucellier–Lipkin Inversor) is an eight-bar linkage constructed from hinged joints that traces a pure straight line from a rotary input. It is named after Charles-Nicolas Peaucellier (1832–1913), a French army officer, and Yom Tov Lipman Lipkin (1846–1876), a Lithuanian Jew and son of the famed Rabbi Israel Salanter.[3][4]

This linkage clearly consists of eight bars when the ground frame is counted as a bar. The Chebychev–Grübler–Kutzbach criterion shows that an eight-bar linkage must have ten single degree-of-freedom joints, while the Peaucellier linkage appears to have only six hinged joints. This is resolved by noting that four of the hinged joints each connect three bars. This is considered to be a special case of two joints that are located in the same place. Thus, six plus four provides the 10 one degree-of-freedom joints.

The Peaucellier linkage is a (4, 4, 0, 0) eight-bar linkage, which means four of the bars have two joints and four bars have three joints.

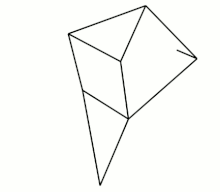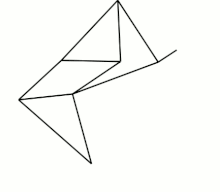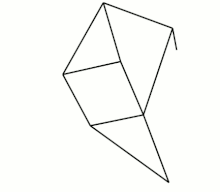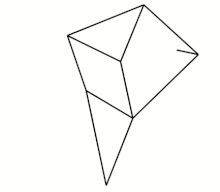
Animation of one leg of Theo Jansen's Strandbeest

The Jansen linkage

The eight bars of the Jansen linkage, which include the ground frame, are readily identified, and include two triangular links. In this case only seven of the 10 hinged joints are readily identified. However, there are three joints that connect three links. The first is the end of the drive crank, the second is the other base pivot and the third is one side of the triangle that forms the lower leg. Separating these overlapping joints provides three additional joints so there are 10 single degree-of-freedom joints.

The Jansen linkage is of type (5, 2, 1, 0), because the upper triangular link supports four joints, two of which overlap at the ground joint, the lower triangular link and the input crank connect three joints and are ternary links. The remaining five links, which includes the ground link, are binary links.

gollark: My laptop's low-capacity SSD can only store two of these "50GB games". I mostly get smaller games without fancy textures or whatever though.
gollark: It's very green.
gollark: Technically, I think distilled water is also pretty nonconductive...
gollark: 'Tis nonconductive.
gollark: No it wouldn't.

References
  1. J. M. McCarthy and G. S. Soh, Geometric Design of Linkages, 2nd Edition, Springer 2010
  2. L. W. Tsai, ''Mechanism design: enumeration of kinematic structures according to function'', CRC Press, 2000. Books.google.com. Retrieved 2013-06-13.
  3. "Mathematical tutorial of the Peaucellier–Lipkin linkage". Kmoddl.library.cornell.edu. Retrieved 2011-12-06.
  4. Taimina, Daina. "How to draw a straight line by Daina Taimina". Kmoddl.library.cornell.edu. Retrieved 2011-12-06.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.