Leg mechanism

A leg mechanism (walking mechanism) is a mechanical system designed to provide a propulsive force by intermittent frictional contact with the ground. This is in contrast with wheels or continuous tracks which are intended to maintain continuous frictional contact with the ground. Mechanical legs are linkages that can have one or more actuators, and can perform simple planar or complex motion. Compared to a wheel, a leg mechanism is potentially better fitted to uneven terrain, as it can step over obstacles.[1].

Theo Jansen's Strandbeest, a group of planar walking mechanisms.

An early design for a leg mechanism called the Plantigrade Machine by Pafnuty Chebyshev was shown at the Exposition Universelle (1878). The original engravings for this leg mechanism are available.[2] The design of the leg mechanism for the Ohio State Adaptive Suspension Vehicle (ASV) is presented in the 1988 book Machines that Walk.[3] In 1996, W-B. Shieh presented a design methodology for leg mechanisms.[4]

The artwork of Theo Jansen[5], see Jansen's linkage, has been particularly inspiring for the design of leg mechanisms, as well as the Klann patent, which is the basis for the leg mechanism of the Mondo Spider.

Design goals
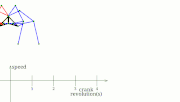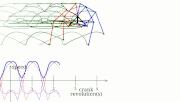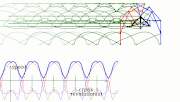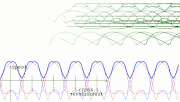
  • horizontal speed as constant as possible while touching the ground (support phase)[1][6]
  • while the foot is not touching the ground, it should move as fast as possible
  • constant torque/force input (or at least no extreme spikes/changes)
  • stride height (enough for clearance, not too much to conserve energy)
  • the foot has to touch the ground for at least half of the cycle for a two/four leg mechanism[1] or respectively, a third of the cycle for a three/six leg mechanism
  • minimized moving mass
  • vertical center of mass always inside the base of support[1]
  • the speed of each leg or group of legs should be separately controllable for steering[6]
  • the leg mechanism should allow forward and backward walking[6]

Another design goal can be, that stride height and length etc. can be controlled by the operator.[6] This can relatively easily be achieved with a hydraulic leg mechanism, but is not practicable with a crank-based leg mechanism.[6]

The optimization has to be done for the whole vehicle – ideally the force/torque variation during a rotation should cancel each other out.[1]

History

Richard Lovell Edgeworth tried in 1770 to construct a machine he called a "Wooden Horse", but was not successful.[7][8]

Patents

Patents for leg mechanism designs range from rotating cranks to four-bar and six-bar linkages.[9] See for example the following patents:

Stationary
  • Jansen linkage
  • Klann linkage
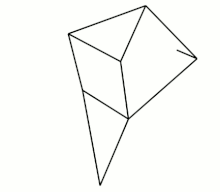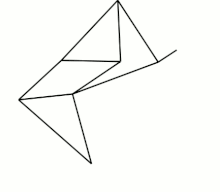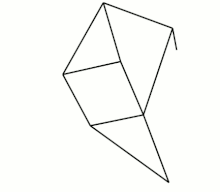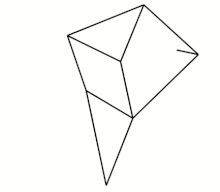
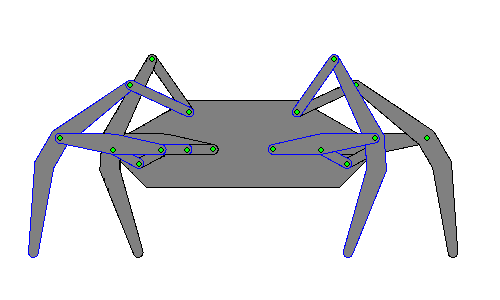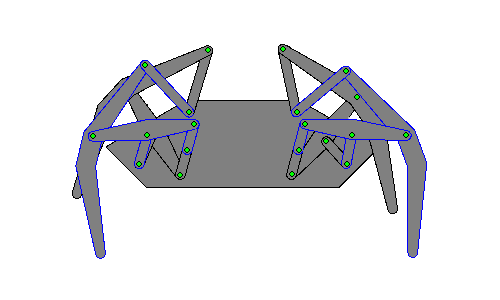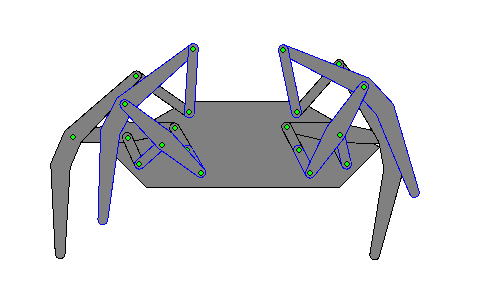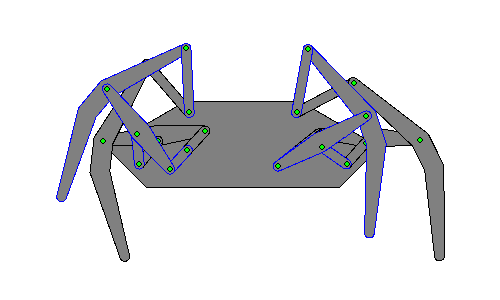
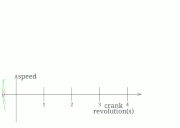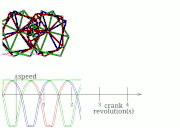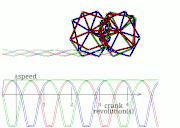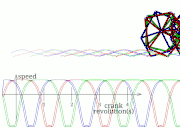
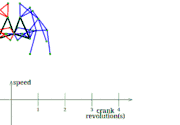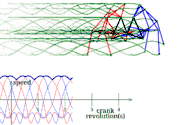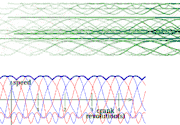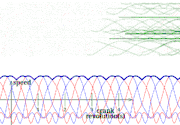
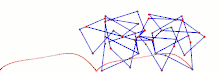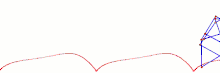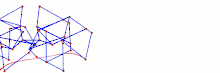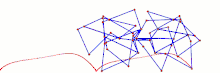
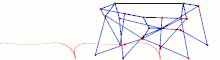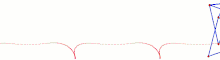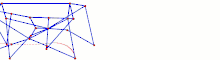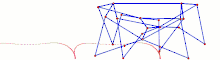
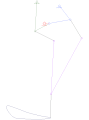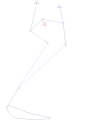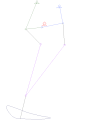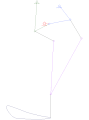  • Eight-bar leg mechanism [10]
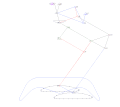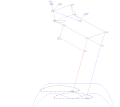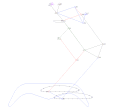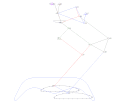  • Tokyo Institute of Technology walking chair[11]
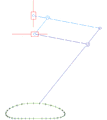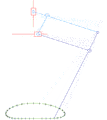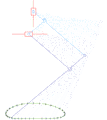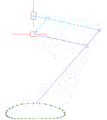  • 2 DOF pantograph leg mechanism[12]
  • 2 DOF leg mechanism of the RPRPR type.[13]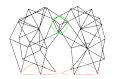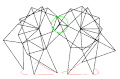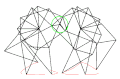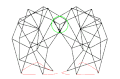
  • Strandbeest (applied Jansen linkage)
  • Ghassaei Linkage[1]
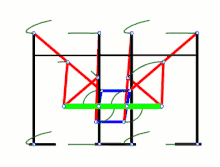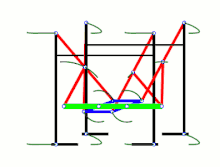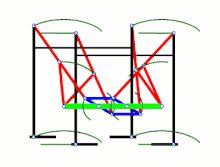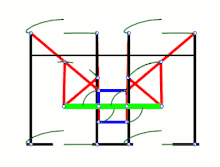  • Tchebyshevs plantigrade machine[14]
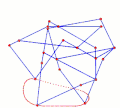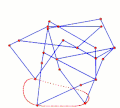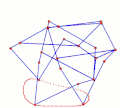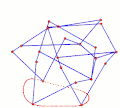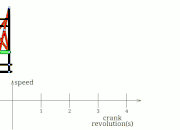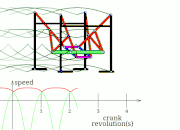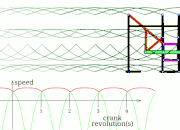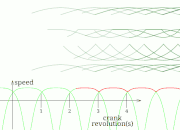
  • TrotBot Linkage (without heel linkage)[15]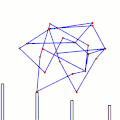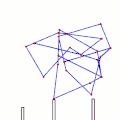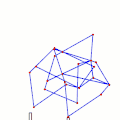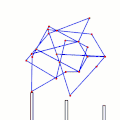
  • TrotBot[16] Linkage Speed Variability as Ground Height Changes
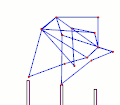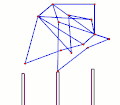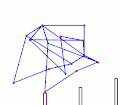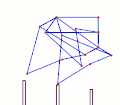  • Strider[16] Linkage Speed Variability as Ground Height Changes
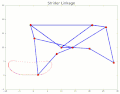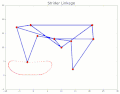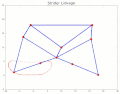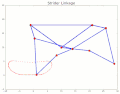  • Strider Linkage[17]
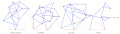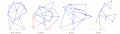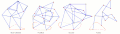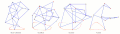  • Foot-Paths of Strandbeest, TrotBot, Strider and Klann Linkages

Walking
* 4 legs 6 legs
Strandbeest
Ghassaei
Klann linkage 1
Klann linkage 2
Plantigrade Mechanism
Trotbot[18]
Strider Linkage[17]
Strider Prototype, 4 legs/side

Complex mechanism

Shown above are only planar mechanisms, but there are also more complex mechanisms:

gollark: It's not obscure, it's pretty commonly known.
gollark: So all we need to do is modify Perl to be parseable, and then the halting problem is solved...
gollark: I have a thing to obfuscate python which produces output like this:```pythonimport zlib,base64,marshal;exec(marshal.loads(zlib.decompress(base64.b85decode("c${5PO>fjN5Vf6T<8HegI8ekXNF3Nh;}%p=P*owS!ilOBAu3-gZ#;Cf<O|zrx6u|ME%*L~?UBEff52bhgq>2UG|{{nKacaCCkeXq_%>eK&_66lByol~?lR$|%O3Y^CYhfHJithL(*KEg4?-EtF-FjnJsHl4twKpVCXh>W%qe)2r9~g;71k2G#j>lqe#^<_Rn(pF7Atba@e+ST!@+OoX@7{@K1?f7$XbI+$Q{3Z8@tZ)js=4zctK|93SU0GAjX?viRa|<{)K1!MKB{X@5<_YMw{pZIz&geDv7Kj*>B0&XxM9ewaT(|#6tz&YS4y<mMAMITED}d9@i$#_;ONK=U>tc%F$%#bI*3QzFTvuKv!j<ZB^Fh*m1v*3a!UKbXyyh7AHF`mE~EHl|l~O1>9{Ac|_Eb&CP?oDI`{;IEfBanSiVnM4NH5J~pP(uNZ^8p2kVSPC@C^DzUAtk$4F&1l!%+%j=`HBr)+ssAj-SUa|OQ`Q%_MG(;OwQsz|#2IA-qoTNq3Np*YA;wJje;;c+W#`IVyU`gWim^)J&P;9+<d}E{%+Q29+V!O$dIAe$JH=cib_f|BNX(N=Wt7df~PDQk4^`rmX3<vz)^{nH6qgI~1y$UR}q|`htbzBKER@l*QGHp=V=^0L?FydIIs`Xt%+k<JUjc#c!zJjH-{Y&T8S>8?k7Et#Qx}BG@&S1yM>4z35aqo&xDJA{u+U9%YFJ<1>Xa"))))```but I think the output only works on the same version/platform.
gollark: I've heard that you can't actually unambiguously parse perl.
gollark: I see.

See also

References
  1. Ghassaei, Amanda (20 April 2011). The Design and Optimization of a Crank-Based Leg Mechanism (PDF) (Thesis). Pomona College. Archived (PDF) from the original on 29 October 2013. Retrieved 27 July 2016.
  2. P. L. Tchebyshev. Plantigrade Machine Engraving. stored in the Musée des arts et métiers du Conservatoire national des arts et métiers Paris, France CNAM 10475-0000.
  3. S. M. Song and K. J. Waldron (November 1988). Machines that Walk: The Adaptive Suspension Vehicle. The MIT Press.
  4. W. B. Shieh (1996). Design and Optimization of Planar Leg Mechanisms Featuring Symmetrical Foot-Point Paths (Thesis). PhD Dissertation, The University of Maryland.
  5. Theo Jansen. Strangdbeest.
  6. Shigley, Joseph E. (September 1960). The Mechanics of Walking Vehicles: A Feasibility Study (PDF) (Report). University of Michigan Department of Mechanical Engineering. Archived (PDF) from the original on 4 March 2016. Retrieved 27 July 2016. Alt URL
  7. Giesbrecht, Daniel (8 April 2010). Design and optimization of a one-degree-of-freedom eight-bar leg mechanism for a walking machine (Thesis). University of Manitoba. hdl:1993/3922.
  8. Uglow, Jenny (2002). The Lunar Men: Five Friends Whose Curiosity Changed the World. New York, New York: Farrar, Strauss and Giroux. ISBN 0-374-19440-8. Retrieved 27 July 2016.
  9. J. Michael McCarthy (March 2019). Kinematic Synthesis of Mechanisms: a project based approach. MDA Press.
  10. Simionescu, P.A.; Tempea, I. (20–24 June 1999). Kinematic and kinetostatic simulation of a leg mechanism (PDF). 10th World Congress on the Theory of Machines and Mechanisms. Oulu, Finland. pp. 572–577. Retrieved 27 July 2016.
  11. Funabashi, H.; Takeda, Y.; Kawabuchi, I.; Higuchi, M. (20–24 June 1999). Development of a walking chair with a self-attitude-adjusting mechanism for stable walking on uneven terrain. 10th World Congress on the Theory of Machines and Mechanisms. Oulu, Finland. pp. 1164–1169.
  12. Simionescu, P.A. (21–24 August 2016). MeKin2D: Suite for Planar Mechanism Kinematics (PDF). ASME 2016 Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Charlotte, NC, USA. pp. 1–10. Retrieved 7 January 2017.
  13. Simionescu, P.A. (2014). Computer Aided Graphing and Simulation Tools for AutoCAD Users (1st ed.). Boca Raton, Florida: CRC Press. ISBN 978-1-4822-5290-3.
  14. http://en.tcheb.ru/1
  15. Vagle, Wade. "TrotBot Linkage Plans". DIYwalkers.
  16. "Shigley's Study Applied". DIYwalkers.
  17. Vagle, Wade. "Strider Linkage Plans". DIYwalkers.
  18. https://www.diywalkers.com/trotbot.html

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.