Counter automaton

In computer science, more particular in the theory of formal languages, a counter automaton, or counter machine, is a pushdown automaton with only two symbols, ${\displaystyle A}$ and the initial symbol in ${\displaystyle \Gamma }$, the finite set of stack symbols.[1]^:171

Diagram of a counter automaton. Each cell of its stack either contains an "A" or a space symbol.

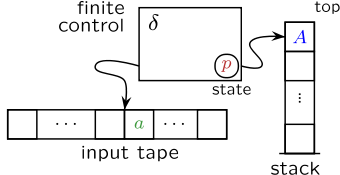
Equivalently, a counter automaton is a nondeterministic finite automaton with an additional memory cell that can hold one nonnegative integer number (of unlimited size), which can be incremented, decremented, and tested for being zero.[2]^:351

Properties

The class of counter automata can recognize a proper superset of the regular[note 1] and a subset of the deterministic context free languages.[2]^:352

For example, the language ${\displaystyle \{a^{n}b^{n}:n\in \mathbb {N} \}}$ is a non-regular[note 2] language accepted by a counter automaton: It can use the symbol ${\displaystyle A}$ to count the number of ${\displaystyle a}$s in a given input string ${\displaystyle x}$ (writing an ${\displaystyle A}$ for each ${\displaystyle a}$ in ${\displaystyle x}$), after that, it can delete an ${\displaystyle A}$ for each ${\displaystyle b}$ in ${\displaystyle x}$.

A two-counter automaton, that is, a two-stack Turing machine with a two-symbol alphabet, can simulate an arbitrary Turing machine.[1]^:172

Notes

1. Every regular language L is accepted by some finite automaton F (see Regular language#Equivalent formalisms). Enriching F with a two-symbol stack which is ignored by F’s control makes it a counter automaton accepting L.
2. by the pumping lemma for regular languages

References

1. John E. Hopcroft and Jeffrey D. Ullman (1979). Introduction to Automata Theory, Languages, and Computation. Reading/MA: Addison-Wesley. ISBN 0-201-02988-X.
2. John E. Hopcroft and Rajeev Motwani and Jeffrey D. Ullman (2003). Introduction to Automata Theory, Languages, and Computation. Upper Saddle River/NJ: Addison Wesley. ISBN 0-201-44124-1.