Completing the square

In elementary algebra, completing the square is a technique for converting a quadratic polynomial of the form

${\displaystyle ax^{2}+bx+c}$

to the form

${\displaystyle a(x-h)^{2}+k}$

for some values of h and k.

Completing the square is used in

• solving quadratic equations,
• deriving the quadratic formula,
• graphing quadratic functions,
• evaluating integrals in calculus, such as Gaussian integrals with a linear term in the exponent,
• finding Laplace transforms.

In mathematics, completing the square is often applied in any computation involving quadratic polynomials.

Overview

Background

The formula in elementary algebra for computing the square of a binomial is:

${\displaystyle (x+p)^{2}\,=\,x^{2}+2px+p^{2}.}$

For example:

${\displaystyle {\begin{alignedat}{2}(x+3)^{2}\,&=\,x^{2}+6x+9&&(p=3)\\[3pt](x-5)^{2}\,&=\,x^{2}-10x+25\qquad &&(p=-5).\end{alignedat}}}$

In any perfect square, the coefficient of x is twice the number p, and the constant term is equal to p².

Basic example

Consider the following quadratic polynomial:

${\displaystyle x^{2}+10x+28.}$

This quadratic is not a perfect square, since 28 is not the square of 5:

${\displaystyle (x+5)^{2}\,=\,x^{2}+10x+25.}$

However, it is possible to write the original quadratic as the sum of this square and a constant:

${\displaystyle x^{2}+10x+28\,=\,(x+5)^{2}+3.}$

This is called completing the square.

General description

Given any monic quadratic

${\displaystyle x^{2}+bx+c,}$

it is possible to form a square that has the same first two terms:

${\displaystyle \left(x+{\tfrac {1}{2}}b\right)^{2}\,=\,x^{2}+bx+{\tfrac {1}{4}}b^{2}.}$

This square differs from the original quadratic only in the value of the constant term. Therefore, we can write

${\displaystyle x^{2}+bx+c\,=\,\left(x+{\tfrac {1}{2}}b\right)^{2}+k,}$

where ${\displaystyle k\,=\,c-{\frac {b^{2}}{4}}}$. This operation is known as completing the square. For example:

${\displaystyle {\begin{alignedat}{1}x^{2}+6x+11\,&=\,(x+3)^{2}+2\\[3pt]x^{2}+14x+30\,&=\,(x+7)^{2}-19\\[3pt]x^{2}-2x+7\,&=\,(x-1)^{2}+6.\end{alignedat}}}$

Non-monic case

Given a quadratic polynomial of the form

${\displaystyle ax^{2}+bx+c}$

it is possible to factor out the coefficient a, and then complete the square for the resulting monic polynomial.

Example:

${\displaystyle {\begin{aligned}3x^{2}+12x+27&=3(x^{2}+4x+9)\\&{}=3\left((x+2)^{2}+5\right)\\&{}=3(x+2)^{2}+15\end{aligned}}}$

This allows us to write any quadratic polynomial in the form

${\displaystyle a(x-h)^{2}+k.}$

Formula

Scalar case

The result of completing the square may be written as a formula. For the general case:[1]

${\displaystyle ax^{2}+bx+c\;=\;a(x-h)^{2}+k,\quad {\text{where}}\quad h=-{\frac {b}{2a}}\quad {\text{and}}\quad k=c-ah^{2}=c-{\frac {b^{2}}{4a}}.}$

Specifically, when a = 1:

${\displaystyle x^{2}+bx+c\;=\;(x-h)^{2}+k,\quad {\text{where}}\quad h=-{\frac {b}{2}}\quad {\text{and}}\quad k=c-{\frac {b^{2}}{4}}.}$

Matrix case

The matrix case looks very similar:

${\displaystyle x^{\mathrm {T} }Ax+x^{\mathrm {T} }b+c=(x-h)^{\mathrm {T} }A(x-h)+k\quad {\text{where}}\quad h=-{\frac {1}{2}}A^{-1}b\quad {\text{and}}\quad k=c-{\frac {1}{4}}b^{\mathrm {T} }A^{-1}b}$

where ${\displaystyle A}$ has to be symmetric.

If ${\displaystyle A}$ is not symmetric the formulae for ${\displaystyle h}$ and ${\displaystyle k}$ have to be generalized to:

${\displaystyle h=-(A+A^{\mathrm {T} })^{-1}b\quad {\text{and}}\quad k=c-h^{\mathrm {T} }Ah=c-b^{\mathrm {T} }(A+A^{\mathrm {T} })^{-1}A(A+A^{\mathrm {T} })^{-1}b}$.

Relation to the graph

Graphs of quadratic functions shifted to the right by h = 0, 5, 10, and 15.

Graphs of quadratic functions shifted upward by k = 0, 5, 10, and 15.

Graphs of quadratic functions shifted upward and to the right by 0, 5, 10, and 15.

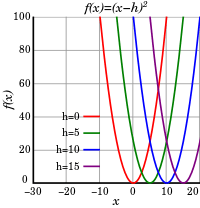
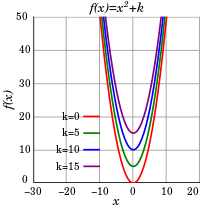
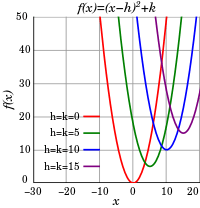
In analytic geometry, the graph of any quadratic function is a parabola in the xy-plane. Given a quadratic polynomial of the form

${\displaystyle (x-h)^{2}+k\quad {\text{or}}\quad a(x-h)^{2}+k}$

the numbers h and k may be interpreted as the Cartesian coordinates of the vertex (or stationary point) of the parabola. That is, h is the x-coordinate of the axis of symmetry (i.e. the axis of symmetry has equation x = h), and k is the minimum value (or maximum value, if a < 0) of the quadratic function.

One way to see this is to note that the graph of the function ƒ(x) = x² is a parabola whose vertex is at the origin (0, 0). Therefore, the graph of the function ƒ(x − h) = (x − h)² is a parabola shifted to the right by h whose vertex is at (h, 0), as shown in the top figure. In contrast, the graph of the function ƒ(x) + k = x² + k is a parabola shifted upward by k whose vertex is at (0, k), as shown in the center figure. Combining both horizontal and vertical shifts yields ƒ(x − h) + k = (x − h)² + k is a parabola shifted to the right by h and upward by k whose vertex is at (h, k), as shown in the bottom figure.

Solving quadratic equations

Completing the square may be used to solve any quadratic equation. For example:

${\displaystyle x^{2}+6x+5=0,}$

The first step is to complete the square:

${\displaystyle (x+3)^{2}-4=0.}$

Next we solve for the squared term:

${\displaystyle (x+3)^{2}=4.}$

Then either

${\displaystyle x+3=-2\quad {\text{or}}\quad x+3=2,}$

and therefore

${\displaystyle x=-5\quad {\text{or}}\quad x=-1.}$

This can be applied to any quadratic equation. When the x² has a coefficient other than 1, the first step is to divide out the equation by this coefficient: for an example see the non-monic case below.

Irrational and complex roots

Unlike methods involving factoring the equation, which is reliable only if the roots are rational, completing the square will find the roots of a quadratic equation even when those roots are irrational or complex. For example, consider the equation

${\displaystyle x^{2}-10x+18=0.}$

Completing the square gives

${\displaystyle (x-5)^{2}-7=0,}$

so

${\displaystyle (x-5)^{2}=7.}$

Then either

${\displaystyle x-5=-{\sqrt {7}}\quad {\text{or}}\quad x-5={\sqrt {7}},}$

In terser language:

${\displaystyle x-5=\pm {\sqrt {7}}.}$

so

${\displaystyle x=5\pm {\sqrt {7}}.}$

Equations with complex roots can be handled in the same way. For example:

${\displaystyle {\begin{array}{c}x^{2}+4x+5\,=\,0\\[6pt](x+2)^{2}+1\,=\,0\\[6pt](x+2)^{2}\,=\,-1\\[6pt]x+2\,=\,\pm i\\[6pt]x\,=\,-2\pm i.\end{array}}}$

Non-monic case

For an equation involving a non-monic quadratic, the first step to solving them is to divide through by the coefficient of x². For example:

${\displaystyle {\begin{array}{c}2x^{2}+7x+6\,=\,0\\[6pt]x^{2}+{\tfrac {7}{2}}x+3\,=\,0\\[6pt]\left(x+{\tfrac {7}{4}}\right)^{2}-{\tfrac {1}{16}}\,=\,0\\[6pt]\left(x+{\tfrac {7}{4}}\right)^{2}\,=\,{\tfrac {1}{16}}\\[6pt]x+{\tfrac {7}{4}}={\tfrac {1}{4}}\quad {\text{or}}\quad x+{\tfrac {7}{4}}=-{\tfrac {1}{4}}\\[6pt]x=-{\tfrac {3}{2}}\quad {\text{or}}\quad x=-2.\end{array}}}$

Applying this procedure to the general form of a quadratic equation leads to the quadratic formula.

Other applications

Integration

Completing the square may be used to evaluate any integral of the form

${\displaystyle \int {\frac {dx}{ax^{2}+bx+c}}}$

using the basic integrals

${\displaystyle \int {\frac {dx}{x^{2}-a^{2}}}={\frac {1}{2a}}\ln \left|{\frac {x-a}{x+a}}\right|+C\quad {\text{and}}\quad \int {\frac {dx}{x^{2}+a^{2}}}={\frac {1}{a}}\arctan \left({\frac {x}{a}}\right)+C.}$

For example, consider the integral

${\displaystyle \int {\frac {dx}{x^{2}+6x+13}}.}$

Completing the square in the denominator gives:

${\displaystyle \int {\frac {dx}{(x+3)^{2}+4}}\,=\,\int {\frac {dx}{(x+3)^{2}+2^{2}}}.}$

This can now be evaluated by using the substitution u = x + 3, which yields

${\displaystyle \int {\frac {dx}{(x+3)^{2}+4}}\,=\,{\frac {1}{2}}\arctan \left({\frac {x+3}{2}}\right)+C.}$

Complex numbers

Consider the expression

${\displaystyle |z|^{2}-b^{*}z-bz^{*}+c,}$

where z and b are complex numbers, z^* and b^* are the complex conjugates of z and b, respectively, and c is a real number. Using the identity |u|² = uu^* we can rewrite this as

${\displaystyle |z-b|^{2}-|b|^{2}+c,}$

which is clearly a real quantity. This is because

${\displaystyle {\begin{aligned}|z-b|^{2}&{}=(z-b)(z-b)^{*}\\&{}=(z-b)(z^{*}-b^{*})\\&{}=zz^{*}-zb^{*}-bz^{*}+bb^{*}\\&{}=|z|^{2}-zb^{*}-bz^{*}+|b|^{2}.\end{aligned}}}$

As another example, the expression

${\displaystyle ax^{2}+by^{2}+c,}$

where a, b, c, x, and y are real numbers, with a > 0 and b > 0, may be expressed in terms of the square of the absolute value of a complex number. Define

${\displaystyle z={\sqrt {a}}\,x+i{\sqrt {b}}\,y.}$

Then

${\displaystyle {\begin{aligned}|z|^{2}&{}=zz^{*}\\&{}=({\sqrt {a}}\,x+i{\sqrt {b}}\,y)({\sqrt {a}}\,x-i{\sqrt {b}}\,y)\\&{}=ax^{2}-i{\sqrt {ab}}\,xy+i{\sqrt {ba}}\,yx-i^{2}by^{2}\\&{}=ax^{2}+by^{2},\end{aligned}}}$

so

${\displaystyle ax^{2}+by^{2}+c=|z|^{2}+c.}$

Idempotent matrix

A matrix M is idempotent when M ² = M. Idempotent matrices generalize the idempotent properties of 0 and 1. The completion of the square method of addressing the equation

${\displaystyle a^{2}+b^{2}=a,}$

shows that some idempotent 2 × 2 matrices are parametrized by a circle in the (a,b)-plane:

The matrix ${\displaystyle {\begin{pmatrix}a&b\\b&1-a\end{pmatrix}}}$ will be idempotent provided ${\displaystyle a^{2}+b^{2}=a,}$ which, upon completing the square, becomes

${\displaystyle (a-{\tfrac {1}{2}})^{2}+b^{2}={\tfrac {1}{4}}.}$

In the (a,b)-plane, this is the equation of a circle with center (1/2, 0) and radius 1/2.

Geometric perspective

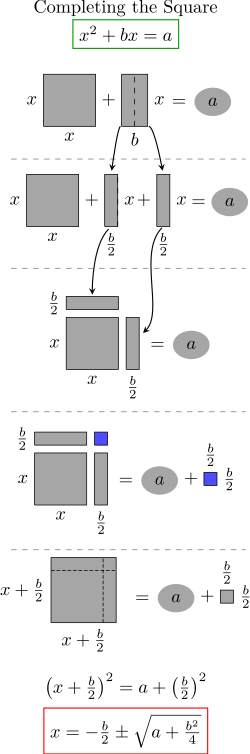
Consider completing the square for the equation

${\displaystyle x^{2}+bx=a.}$

Since x² represents the area of a square with side of length x, and bx represents the area of a rectangle with sides b and x, the process of completing the square can be viewed as visual manipulation of rectangles.

Simple attempts to combine the x² and the bx rectangles into a larger square result in a missing corner. The term (b/2)² added to each side of the above equation is precisely the area of the missing corner, whence derives the terminology "completing the square".

A variation on the technique

As conventionally taught, completing the square consists of adding the third term, v ² to

${\displaystyle u^{2}+2uv}$

to get a square. There are also cases in which one can add the middle term, either 2uv or −2uv, to

${\displaystyle u^{2}+v^{2}}$

to get a square.

Example: the sum of a positive number and its reciprocal

By writing

${\displaystyle {\begin{aligned}x+{1 \over x}&{}=\left(x-2+{1 \over x}\right)+2\\&{}=\left({\sqrt {x}}-{1 \over {\sqrt {x}}}\right)^{2}+2\end{aligned}}}$

we show that the sum of a positive number x and its reciprocal is always greater than or equal to 2. The square of a real expression is always greater than or equal to zero, which gives the stated bound; and here we achieve 2 just when x is 1, causing the square to vanish.

Example: factoring a simple quartic polynomial

Consider the problem of factoring the polynomial

${\displaystyle x^{4}+324.}$

This is

${\displaystyle (x^{2})^{2}+(18)^{2},}$

so the middle term is 2(x²)(18) = 36x². Thus we get

${\displaystyle {\begin{aligned}x^{4}+324&{}=(x^{4}+36x^{2}+324)-36x^{2}\\&{}=(x^{2}+18)^{2}-(6x)^{2}={\text{a difference of two squares}}\\&{}=(x^{2}+18+6x)(x^{2}+18-6x)\\&{}=(x^{2}+6x+18)(x^{2}-6x+18)\end{aligned}}}$

(the last line being added merely to follow the convention of decreasing degrees of terms).

The same argument shows that ${\displaystyle x^{4}+4a^{2}}$ is always factorizable as

${\displaystyle x^{4}+4a^{4}=(x^{2}+2ax+2a^{2})(x^{2}-2ax+2a^{2})}$

(here ${\displaystyle a=3}$).

References

1. Narasimhan, Revathi (2008). Precalculus: Building Concepts and Connections. Cengage Learning. pp. 133–134. ISBN 0-618-41301-4., Section Formula for the Vertex of a Quadratic Function, page 133–134, figure 2.4.8

• Algebra 1, Glencoe, ISBN 0-07-825083-8, pages 539–544
• Algebra 2, Saxon, ISBN 0-939798-62-X, pages 214–214, 241–242, 256–257, 398–401

External links

• "Completing the square". PlanetMath.