Coequalizer

In category theory, a coequalizer (or coequaliser) is a generalization of a quotient by an equivalence relation to objects in an arbitrary category. It is the categorical construction dual to the equalizer.

Definition

A coequalizer is a colimit of the diagram consisting of two objects X and Y and two parallel morphisms f, g : X → Y.

More explicitly, a coequalizer can be defined as an object Q together with a morphism q : Y → Q such that q ∘ f = q ∘ g. Moreover, the pair (Q, q) must be universal in the sense that given any other such pair (Q′, q′) there exists a unique morphism u : Q → Q′ such that u ∘ q = q′. This information can be captured by the following commutative diagram:

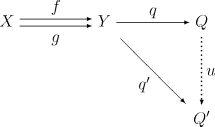
As with all universal constructions, a coequalizer, if it exists, is unique up to a unique isomorphism (this is why, by abuse of language, one sometimes speaks of "the" coequalizer of two parallel arrows).

It can be shown that a coequalizer q is an epimorphism in any category.

Examples
  • In the category of sets, the coequalizer of two functions f, g : X → Y is the quotient of Y by the smallest equivalence relation such that for every , we have .[1] In particular, if R is an equivalence relation on a set Y, and r1, r2 are the natural projections (R ⊂ Y × Y) → Y then the coequalizer of r1 and r2 is the quotient set Y/R. (See also: quotient by an equivalence relation.)
  • The coequalizer in the category of groups is very similar. Here if f, g : X → Y are group homomorphisms, their coequalizer is the quotient of Y by the normal closure of the set
  • For abelian groups the coequalizer is particularly simple. It is just the factor group Y / im(f – g). (This is the cokernel of the morphism f – g; see the next section).
  • In the category of topological spaces, the circle object can be viewed as the coequalizer of the two inclusion maps from the standard 0-simplex to the standard 1-simplex.
  • Coequalisers can be large: There are exactly two functors from the category 1 having one object and one identity arrow, to the category 2 with two objects and one non-identity arrow going between them. The coequaliser of these two functors is the monoid of natural numbers under addition, considered as a one-object category. In particular, this shows that while every coequalising arrow is epic, it is not necessarily surjective.

Properties
  • Every coequalizer is an epimorphism.
  • In a topos, every epimorphism is the coequalizer of its kernel pair.

Special cases

In categories with zero morphisms, one can define a cokernel of a morphism f as the coequalizer of f and the parallel zero morphism.

In preadditive categories it makes sense to add and subtract morphisms (the hom-sets actually form abelian groups). In such categories, one can define the coequalizer of two morphisms f and g as the cokernel of their difference:

coeq(f, g) = coker(g – f).

A stronger notion is that of an absolute coequalizer, this is a coequalizer that is preserved under all functors. Formally, an absolute coequalizer of a pair of parallel arrows f, g : X → Y in a category C is a coequalizer as defined above, but with the added property that given any functor F: C → D, F(Q) together with F(q) is the coequalizer of F(f) and F(g) in the category D. Split coequalizers are examples of absolute coequalizers.

gollark: Did the server crash?
gollark: I can't seem to actually interact *or* chat.
gollark: I'll relog™.
gollark: I can't seem to actually use chat.
gollark: Initiating "Mine craft version one point eighteen point two".

See also

Notes
  1. Barr, Michael; Wells, Charles (1998). Category theory for computing science (PDF). p. 278. Archived from the original (PDF) on 2016-03-04. Retrieved 2013-07-25.

References
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.