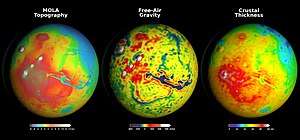
Gravity of Mars

The gravity of Mars is a natural phenomenon, due to the law of gravity, or gravitation, by which all things with mass around the planet Mars are brought towards it. It is weaker than Earth's gravity due to the planet's smaller mass. The average gravitational acceleration on Mars is 3.72076 ms⁻² (about 38% of that of Earth) and it varies laterally.[1] In general, topography-controlled isostasy drives the short wavelength free-air gravity anomalies.[2] At the same time, convective flow and finite strength of the mantle lead to long-wavelength planetary-scale free-air gravity anomalies over the entire planet.[3][4] Variation in crustal thickness, magmatic and volcanic activities, impact-induced Moho-uplift, seasonal variation of polar ice caps, atmospheric mass variation and variation of porosity of the crust could also correlate to the lateral variations.[5][6][7][8][9] Over the years models consisting of an increasing but limited number of spherical harmonics have been produced. Maps produced have included free-air gravity anomaly, Bouguer gravity anomaly, and crustal thickness. In some areas of Mars there is a correlation between gravity anomalies and topography. Given the known topography, higher resolution gravity field can be inferred. Tidal deformation of Mars by the Sun or Phobos can be measured by its gravity. This reveals how stiff the interior is, and shows that the core is partially liquid. The study of surface gravity of Mars can therefore yield information about different features and provide beneficial information for future landing projects.

Measurement

Rotating spherical harmonic, with ${\displaystyle l}$ = 0 to 4 for the vertical, and ${\displaystyle m}$ = 0 to 4 for the horizontal. For the Martian C₂₀ and C₃₀, they vary with time because of the seasonal variation of mass of the polar ice caps through the annual sublimation-condensation cycle of carbon dioxide.

To understand the gravity of Mars, its gravitational field strength g and gravitational potential U are often measured. Simply, if Mars is assumed to be a static perfectly spherical body of radius R_M, provided that there is only one satellite revolving around Mars in a circular orbit and such gravitation interaction is the only force acting in the system, the equation would be,

${\displaystyle {\frac {GMm}{r^{2}}}=mr\omega ^{2}}$,

where G is the universal constant of gravitation (commonly taken as G = 6.674 x 10⁻¹¹ m³ kg⁻¹ s⁻²),[10] M is the mass of Mars (most updated value: 6.41693 x 10²³ kg),[11] m is the mass of the satellite, r is the distance between Mars and the satellite, and ${\displaystyle \omega }$ is the angular velocity of the satellite, which is also equivalent to ${\displaystyle {\frac {2\pi }{T}}}$ (T is the orbiting period of the satellite).

Therefore, ${\displaystyle g={\frac {GM}{R_{M}^{2}}}={\frac {r^{3}\omega ^{2}}{R_{M}^{2}}}={\frac {4r^{3}\pi ^{2}}{T^{2}R_{M}^{2}}}}$, where R_M is the radius of Mars. With proper measurement, r, T and R_M are obtainable parameters from Earth.

However, as Mars is a generic, non-spherical planetary body and influenced by complex geological processes, more accurately, the gravitational potential is described with spherical harmonic functions, following convention in geodesy, see Geopotential_model.

${\displaystyle U(r,\lambda ,\psi )=-{\frac {GM}{r}}\left(1+\textstyle \sum _{l=2}^{l=L}\displaystyle \left({\frac {R}{r}}\right)^{l}\left(C_{l0}P_{l}^{0}(\sin \ \psi )+\sum _{m=1}^{+l}(C_{lm}\cos \ m\lambda +S_{lm}\sin \ m\lambda )P_{l}^{m}(\sin \ \psi )\right)\right)}$,[12]

where ${\displaystyle r,\psi ,\lambda }$ are spherical coordinates of the test point.[12] ${\displaystyle \lambda }$ is longitude and ${\displaystyle \psi }$ is latitude. ${\displaystyle C_{lm}}$ and ${\displaystyle S_{lm}}$ are dimensionless harmonic coefficients of degree ${\displaystyle l}$ and order ${\displaystyle m}$.[12] ${\displaystyle P_{l}^{m}}$ is the Legendre polynomial of degree ${\displaystyle l}$ with ${\displaystyle m=0}$ and is the associated Legendre polynomial with ${\displaystyle m>0}$. These are used to describe solutions of Laplace's equation.[12] ${\displaystyle R}$ is the mean radius of the planet.[12] The coefficient ${\displaystyle C_{l0}}$ is sometimes written as ${\displaystyle J_{n}}$.

1. The lower the degree ${\displaystyle l}$ and order ${\displaystyle m}$, the longer wavelength of anomaly it represents. In turn, long-wavelength gravity anomaly is influenced by global geophysical structures.
2. The higher the degree ${\displaystyle l}$ and order ${\displaystyle m}$, the shorter wavelength of anomaly it represents. For degree over 50, it has been shown that those variations have high correlation with the topography.[13] Geophysical interpretation of surface features could further help deriving a more complete picture of the Martian gravity field, though misleading results could be produced.[13]

The oldest technique in determining the gravity of Mars is through Earth-based observation. Later with the arrival of unmanned spacecraft, subsequent gravity models were developed from radio tracking data.

Earth-based observation

Before the arrival of the Mariner 9 and Viking orbiter spacecraft at Mars, only an estimate of the Mars gravitational constant GM, i.e. the universal constant of gravitation times the mass of Mars, was available for deducing the properties of the Martian gravity field.[14] GM could be obtained through observations of the motions of the natural satellites of Mars (Phobos and Deimos) and spacecraft flybys of Mars (Mariner 4 and Mariner 6).[14]

Long term Earth-based observations of the motions of Phobos and Deimos provide physical parameters including semi-major axis, eccentricity, inclination angle to the Laplacian plane etc.,[15] which allow calculation of the ratio of solar mass to the mass of Mars, moment of inertia and coefficient of the gravitational potential of Mars, and give initial estimates of the gravity field of Mars.[15]

Inferred from radio tracking data

Three-way Doppler, with signal transmitter and receiver separated

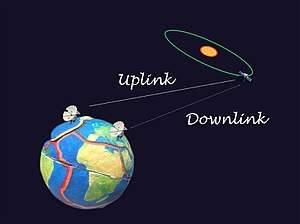
Precise tracking of spacecraft is of prime importance for accurate gravity modeling, as gravity models are developed from observing tiny perturbation of spacecraft, i.e. small variation in velocity and altitude. The tracking is done basically by the antennae of the Deep Space Network (DSN), with one-way, two-way and three-way Doppler and range tracking applied.[16] One-way tracking means the data is transmitted in one way to the DSN from the spacecraft, while two-way and three-way involve transmitting signals from Earth to the spacecraft (uplink), and thereafter transponded coherently back to the Earth (downlink).[16] The difference between two-way and three-way tracking is, the former one has the same signal transmitter and receiver on Earth, while the latter one has the transmitter and receiver at different locations on Earth.[16] The use of these three types of tracking data enhances the coverage and quality of the data, as one could fill in the data gap of another.[16]

Doppler tracking is a common technique in tracking the spacecraft, utilizing radial velocity method, which involves detection of Doppler shifts.[13] As the spacecraft moves away from us along line of sight, there would be redshift of signal, while for the reverse, there would be blueshift of signal. Such technique has also been applied for observation of the motion of exoplanets.[17] While for the range tracking, it is done through measurement of round trip propagation time of the signal.[13] Combination of Doppler shift and range observation promotes higher tracking accuracy of the spacecraft.

The tracking data would then be converted to develop global gravity models using the spherical harmonic equation displayed above. However, further elimination of the effects due to affect of solid tide, various relativistic effects due to the Sun, Jupiter and Saturn, non-conservative forces (e.g. angular momentum desaturations (AMD), atmospheric drag and solar radiation pressure) have to be done,[13] otherwise, considerable errors result.

History

The latest gravity model for Mars is the Goddard Mars Model 3 (GMM-3), produced in 2016, with spherical harmonics solution up to degree and order 120.[13] This model is developed from 16 years of radio tracking data from Mars Global Surveyor (MGS), Mars Odyssey and Mars Reconnaissance Orbiter (MRO), as well as the MOLA topography model and provides a global resolution of 115 km.[13] A separate free-air gravity anomaly map, Bouguer gravity anomaly map and a map of crustal thickness were produced along with this model.[13] Compared with MRO110C and other previous models, major improvement of the estimation of the gravity field comes from more careful modeling of the non-conservative forces applied to the spacecraft.[13]

Gravity solutions	Authors	Year	Degree (m) and order (l) of the spherical harmonic solution [Surface resolution (km)]	Data source
–	JP Gapcynski, RH Tolson and WH Michael Jr	1977	6[18]	Tracking data of Mariner 9, Viking 1 and 2 spacecraft[18]
Geoide martien[19]	G Balmino, B Moynot and N Vales	1982	18[19] [¬600 km]	Tracking data of Mariner 9, Viking 1 and 2 spacecraft[19]
GMM-1[20]	DE Smith, FJ Lerch, RS Nerem, MT Zuber, GB Patel, SK Fricke and FG Lemoine	1993	50[20] [200–300 km]	Tracking data of Mariner 9, Viking 1 and 2 spacecraft[20]
Mars50c[21]	AS Konopliv, WL Sjogren	1995	50[21]	Tracking data of Mariner 9, Viking 1 and 2 spacecraft[21]
GMM-2B[14]	FG Lemoine, DE Smith, DD Rowlands, MT Zuber, GA Neumann, DS Chinn, and DE Pavlis	2001	80[14]	Tracking data of Mars Global Surveyor (MGS), and MOLA-derived topography data [14]
GGM1041C[22]	FG Lemoine	2001	90[22]	Tracking data of Mars Global Surveyor (MGS) and Mars Odyssey, and MOLA-derived topography data[22]
MGS95J[23]	AS Konopliv, CF Yoder, EM Standish, DN Yuan, WL Sjogren	2006	95[23] [~112 km]	Tracking data of Mars Global Surveyor (MGS) and Mars Odyssey, and MOLA-derived topography data [23]
MGGM08A[7]	JC Marty, G Balmino, J Duron, P Rosenblatt, S Le Maistre, A Rivoldini, V Dehant, T. Van Hoolst	2009	95[7] [~112 km]	Tracking data of Mars Global Surveyor (MGS) and Mars Odyssey, and MOLA-derived topography data[7]
MRO110B2[24]	AS Konopliv, SW Asmar, WM Folkner, Ö Karatekin, DC Nunes, SE Smrekar, CF Yoder, MT Zuber	2011	110[24]	Tracking data of Mars Global Surveyor (MGS), Mars Odyssey and Mars Reconnaissance Orbiter (MRO), and MOLA-derived topography data[24]
MGM2011[1]	C Hirt, SJ Claessens, M Kuhn, WE Featherstone	2012	[3 km (equator) – 125 km][1]	Gravity solution MRO110B2, and MOLA-derived topography data[1]
GMM-3[13]	A Genova, S Goossens, FG Lemoine, E Mazarico, GA Neumann, DE Smith, MT Zuber	2016	120[13] [115 km]	Mars Global Surveyor (MGS), Mars Odyssey and Mars Reconnaissance Orbiter (MRO)[13] MGS (SPO-1, SPO-2, GCO, MAP)[13] ODY (ODYT, ODYM)[13] MRO (MROT, MROM)[13]

The techniques in tracking the spacecraft and geophysical interpretation of surface features can affect the resolution of the strength of gravity field. The better technique favors spherical harmonic solutions to higher degrees and orders. Independent analysis on Mariner 9 and Viking Orbiter tracking data yielded a degree and order of 6 spherical harmonic solution.,[18] Further combination of the two data sets, along with correlation of anomalies with volcanic features (positive anomaly) and deep-printed depression (negative anomaly) assisted by image data allows a degree and order of 18 spherical harmonic solution produced.[19] Further use of spatial a priori constraint method, which had taken the topography into account in solving the Kaula power law constraint, had favored model of up to degree 50 spherical harmonic solution in global resolution (Goddard Mars Model-1, or GMM-1)[20] then the subsequent models with higher completeness and degree and order up to 120 for the latest GMM-3.[13]

Mars free-air gravity map produced along with the GMM-3 gravity solution[13] (Red: gravity high; Blue: gravity low) (Credit: NASA's Scientific Visualization Studio)

Therefore, gravity models nowadays are not directly produced through transfer of the measured gravity data to any spatial information system because there is difficulty in producing model with sufficiently high resolution. Topography data obtained from the MOLA instrument aboard the Mars Global Surveyor thus becomes a useful tool in producing a more detailed short-scale gravity model, utilizing the gravity-topography correlation in short-wavelength.[13] However, not all regions on Mars show such correlation, notably the northern lowland and the poles.[13] Misleading results could be easily produced, which could lead to wrong geophysics interpretation.[13]

The later modifications of gravity model include taking other non-conservative forces acting on spacecraft into account, including atmospheric drag, solar radiation pressure, Mars reflected solar radiation pressure, Mars thermal emission, and spacecraft thrusting which despins or desaturates the angular moment wheels.[14] In addition, Martian precession and third body attraction due to the Sun, Moon and planets, which could affect the spacecraft orbit, as well as relavistic effects on the measurements should also be corrected.[7] These factors could lead to offset of the true gravity field. Accurate modeling is thus required to eliminate the offset. Such work is still ongoing.

Static gravity field

Many researchers have outlined the correlation between short-wavelength (locally varying) free-air gravity anomalies and topography. For regions with higher correlation, free-air gravity anomalies could be expanded to higher degree strength through geophysical interpretation of surface features,[13] so that the gravity map could offer higher resolution. It has been found that the southern highland has high gravity/topography correlation but not for the northern lowland.[13] Therefore, the resolution of free-air gravity anomaly model typically has higher resolution for the southern hemisphere, as high as over 100 km.[13]

Free-air gravity anomalies are relatively easier to measure than the Bouguer anomalies as long as topography data is available because it does not need to eliminate the gravitational effect due to the effect of mass surplus or deficit of the terrain after the gravity is reduced to sea level. However, to interpret the crustal structure, further elimination of such gravitational effect is necessary so that the reduced gravity would only be the result of the core, mantle and crust below datum.[5] The product after elimination is the Bouguer anomalies. However, density of the material in building up the terrain would be the most important constraint in the calculation, which may vary laterally on the planet and is affected by porosity and geochemistry of the rock.[5][9] Relevant information could be obtained from Martian meteorites and in-situ analysis.

Local gravity anomalies

The crust-mantle boundary variation, intrusion, volcanism and topography can bring effect to the orbit of spacecraft, due to the higher density of mantle and volcanic material and lower density of the crust. (Not in scale) +ve: Positive anomaly; -ve: Negative anomaly

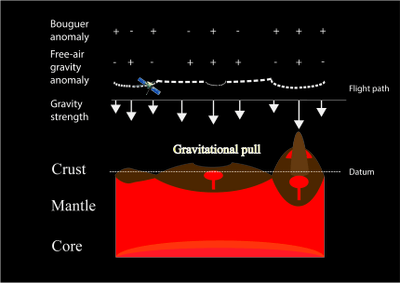
Since Bouguer gravity anomalies have strong link with depth of crust-mantle boundary, one with positive Bouguer anomalies may mean that it has a thinner crust composed of lower density material and is influenced more strongly by the denser mantle, and vice versa. However, it could also be contributed by the difference in density of the erupted volcanic load and sedimentary load, as well as subsurface intrusion and removal of material.[5][6][25] Many of these anomalies are associated with either geological or topographic features.[5] Few exception includes the 63°E, 71°N anomaly,[5] which may represent an extensive buried structure as large as over 600 km, predated the early-Noachian buried surface.[5]

Topography anomalies

Strong correlation between topography and short-wavelength free-air gravity anomalies has been shown for both study of the gravity field of the Earth and the Moon,[2] and it can be explained by the wide occurrence of isostasy.[2][26] High correlation is expected for degree over 50 (short-wavelength anomaly) on Mars.[13] And it could be as high as 0.9 for degrees between 70 and 85.[13] Such correlation could be explained by flexural compensation of topographic loads.[2][26] It is noted that older regions on Mars are isostatically compensated when the younger region are usually only partially compensated.[13]

Anomalies from volcanic constructs

Mars Bouguer gravity map, produced along with GMM-3 gravity solution in 2016[13](Red: gravity high; Blue: gravity low) (Credit: NASA's Scientific Visualization Studio)

Different volcanic constructs could behave differently in terms of gravity anomalies. Large volcanoes Olympus Mons and the Tharsis Montes produce the largest positive free-air gravity anomalies in the solar system.[5] Alba Patera, also a volcanic rise, north of the Tharsis Montes, however, produces negative Bouguer anomaly, though its extension is similar to that of Olympus Mons.[5] And for the Elysium Mons, its center is found to have slight increase in Bouguer anomalies in an overall broad negative anomaly context in the Elysium rise.[5]

The knowledge of anomaly of volcanoes, along with density of the volcanic material, would be useful in determining the lithospheric composition and crustal evolution of different volcanic edifices.[27] It has been suggested that the extruded lava could range from andesite (low density) to basaltic (high density) and the composition could change during the construction of the volcanic shield, which contributes to the anomaly.[27] Another scenario is it is possible for high density material intruded beneath the volcano.[27][6] Such setting has already been observed over the famous Syrtis major, which has been inferred to have an extinct magma chamber with 3300 kg m³ underlying the volcano, evident from positive Bouguer anomaly.[6]

Anomalies from depressions

Different depressions also behave differently in Bouguer anomaly. Giant impact basins like Argyre, Isidis, Hellas and Utopia basins also exhibit very strong positive Bouguer anomalies in circular manner.[5] These basins have been debated for their impact crater origin. If they are, the positive anomalies may be due to uplift of Moho, crustal thinning and modification events by sedimentary and volcanic surface loads after impacting.[5][25]

But at the same time there are also some large basins that are not associated with such positive Bouguer anomaly, for example, Daedalia, northern Tharsis and Elysium, which are believed to be underlain by the northern lowland plain.[5]

In addition, certain portions of Coprates, Eos Chasma and Kasei Valles are also found to have positive Bouguer anomalies,[5] though they are topographic depressions. This may suggest that these depressions are underlain by shallow dense intrusion body.[5]

Global gravity anomalies

Global gravity anomalies, also termed as long-wavelength gravity anomalies, are the low-degree harmonics of the gravity field,[4] which cannot be attributed to local isostasy, but rather finite strength of the mantle and density differences in the convection current.[13][3][4] For Mars, the largest component of Bouguer anomaly is the degree one harmonic, which represents the mass deficit in the southern hemisphere and excess in the northern hemisphere.[5] The second largest component corresponds to the planet flattening and Tharsis bulge.[5]

Early study of the geoid in the 1950s and 1960s has focused on the low-degree harmonics of the Earth's gravity field in order to understand its interior structure.[4] It has been suggested that such long-wavelength anomalies on Earth could be contributed by the sources located in deep mantle and not in the crust, for example, caused by the density differences in driving the convection current,[4][28] which has been evolving with time. The correlation between certain topography anomalies and long-wavelength gravity anomalies, for example, the mid-Atlantic ridge and Carlsberg ridge, which are topography high and gravity high on the ocean floor, thus became the argument for the convection current idea on Earth in the 1970s,[29][30] though such correlations are weak in the global picture.

Another possible explanation for the global scale anomalies is the finite strength of the mantle (in contrast to zero stress), which makes the gravity deviated from hydrostatic equilibrium.[3] For this theory, because of the finite strength, flow may not exist for most of the region that are understressed.[3] And the variations of density of the deep mantle could be the result of chemical inhomogeneities associated with continent separations,[3] and scars left on Earth after the torn away of the moon.[3] These are the cases suggested to work when slow flow is allowed to happen under certain circumstances.[3] However, it has been argued that the theory may not be physically feasible.[4]

Time-variable gravity field

Sublimation-condensation cycle occurs on Mars which results in carbon dioxide exchange between the cryosphere and the atmosphere. In turn, there is exchange in mass between the two spheres, which gives seasonal variation of gravity. (Courtesy NASA/JPL-Caltech)

Seasonal change of gravity field at the poles

The sublimation-condensation cycle of carbon dioxide on Mars between the atmosphere and cryosphere (polar ice cap) operates seasonally.[8] This cycle contributes as almost the only variable accounting for changes in gravity field on Mars.[8] The measured gravitational potential of Mars from orbiters could be generalized as the equation below,

${\displaystyle V(Mars)=V({Solid\,planet})+V(Seasonal\,caps+Atmosphere)}$[8]

In turn, when there is more mass in the seasonal caps due to the more condensation of carbon dioxide from the atmosphere, the mass of the atmosphere would drop. They have inverse relationship with each other. And the change in mass has direct effect towards the measured gravitational potential.

The seasonal mass exchange between the northern polar cap and southern polar cap exhibits long-wavelength gravity variation with time.[8][13] Long years of continuous observation has found that the determination of even zonal, normalized gravity coefficient C_{l=2, m=0}, and odd zonal, normalized gravity coefficient C_{l=3, m=0} are crucial for outlining the time-variable gravity due to such mass exchange,[24][8][31][32] where ${\displaystyle l}$ is the degree while ${\displaystyle m}$ is the order. More commonly, they are represented in form of C_lm in research papers.

If we regard the two poles as two distinct point masses, then, their masses are defined as,

${\displaystyle M_{NP}={\frac {C_{20}+C_{30}}{2}}\,M_{Mars}}$[32]

${\displaystyle M_{SP}={\frac {C_{20}-C_{30}}{2}}\,M_{Mars}}$[32]

Data has indicated that the maximum mass variation of the southern polar cap is approximately 8.4 x 10¹⁵ kg,[13] occurring near the autumnal equinox,[13] while for that of the northern polar is approximately 6.2 x 10¹⁵ kg,[13] occurring in between the winter solstice and spring equinox.[13]

In long term speaking, it has been found that the mass of ice stored in North Pole would increase by (1.4 ± 0.5) x 10¹¹ kg,[8] while in South Pole it would decrease by (0.8 ± 0.6) x 10¹¹ kg.[8] In addition, the atmosphere would have decrease in term of the mass of carbon dioxide by (0.6 ± 0.6) x 10¹¹ kg in long term as well.[8] Due to existence of uncertainties, it is unclear whether migration of material from the South Pole to the North Pole is ongoing, though such a possibility cannot be ruled out.[8]

Tide

The two major tidal forces acting on Mars are the solar tide and Phobos tide.[13] Love number k₂ is an important proportional dimensionless constant relating the tidal field acting to the body with the multipolar moment resulting from the mass distribution of the body. Usually k₂ can tell quadrupolar deformation.[13] Finding k₂ is helpful in understanding the interior structure on Mars.[13] The most updated k₂ obtained by Genova's team is 0.1697 ± 0.0009.[13] As if k₂ is smaller than 0.10 a solid core would be indicated, this tells that at least the outer core is liquid on Mars,[31] and the predicted core radius is 1520–1840 km.[31]

However, current radio tracking data from MGS, ODY and MRO does not allow the effect of phase lag on the tides to be detected because it is too weak and needs more precise measurement on the perturbation of spacecraft in the future.[13]

Geophysical implications

Crustal thickness

No direct measurement of crustal thickness on Mars is currently available. Geochemical implications from SNC meteorites and orthopyroxenite meteorite ALH84001 suggested that mean crustal thickness of Mars is 100–250 km.[33] Viscous relaxation analysis suggested that the maximum thickness is 50–100 km. Such thickness is critical in maintaining hemispheric crustal variations and preventing channel flow.[34] Combination studies on geophysics and geochemistry suggested that average crustal thickness could be down to 50 ± 12 km.[35]

Measurement of gravity field by different orbiters allows higher-resolution global Bouguer potential model to be produced.[5] With local shallow density anomalies and effect of core flattening eliminated,[5] the residual Bouguer potential is produced, as indicated by the following equation,

${\displaystyle U_{RB}=U_{B}-U_{core}-U_{local}}$[5]

Histogram of percentage area against crustal thickness of Mars: 32 km and 58 km are the two major peaks of the histogram.

The residual Bouguer potential is contributed by the mantle.[5] The undulation of the crust-mantle boundary, or the Moho surface, with mass of terrain corrected, should have resulted in varying residual anomaly.[5] In turn, if undulating boundary is observed, there should be changes in crustal thickness.

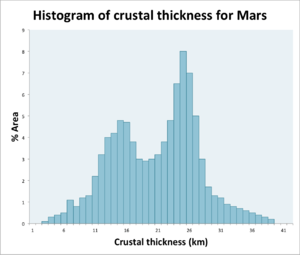
Global study of residual Bouguer anomaly data indicates that crustal thickness of Mars varies from 5.8 km to 102 km.[5] Two major peaks at 32 km and 58 km are identified from an equal-area histogram of crustal thickness.[5] These two peaks are linked to the crustal dichotomy of Mars.[5] Almost all the crust thicker than 60 km are contributed by the southern highland, with generally uniform thickness.[5] And the northern lowland in general has thinner crust. The crustal thickness of the Arabia Terra region and northern hemisphere are found to be latitude-dependent.[5] The more southward towards the Sinai Planum and Lunae Planum, the more thickened the crust is.[5]

Comparison of topography, free-air gravity anomaly and crustal density map – Red: gravity high; Blue: gravity low

Among all regions, the Thaumasia and Claritis contain the thickest portion of crust on Mars that account for the histogram > 70 km.[5] The Hellas and Argyre basins are observed to have crust thinner than 30 km,[5] which are the exceptionally thin area in the southern hemisphere.[5] Isidis and Utopia are also observed to have significant crustal thinning,[5] with the center of Isidis basins believed to have the thinnest crust on Mars.[5]

Crust redistribution by impacting and viscous relaxation

After the initial impact, high heat flux and high water content would have favored viscous relaxation to take place. The crust becomes more ductile. The basin topography of the craters is thus subjected to greater stress due to self-gravitation, which further drive crustal flow and decay of relief. However, this analysis may not work for giant impact craters such as Hellas, Utopia, Argyre and Isidis basins.[25]

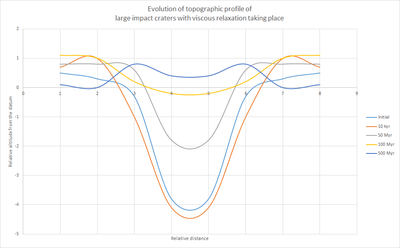
Crustal thinning is believed to have taken place underneath almost all the major impact craters.[5] Crustal excavation, modification through emplacement of volcanic material and crustal flow taking place in the weak lithosphere are the possible causes.[5] With the pre-impact crust excavated, gravitational restoration would take place through central mantle uplift, so that the mass deficit of cavity could be compensated by the mass of the uplifted denser material.[5]

Giant impact basins Utopia, Hellas, Argyre and Isidis are some of the most prominent examples.[5] Utopia, an impact basin located in northern lowland, is filled by light and water-deposited sedimentary material and has slightly thickened crust at the center.[5] This is potentially due to large resurfacing process in the northern lowland.[5] While for Hellas, Argyre and Isidis basins, they have great Moho uplifted relief and exhibit annuli of diffuse thickened crust beyond the crustal rim.[5]

But on the contrary, almost all the Martian basins with diameter of 275 km < D < 1000 km are associated with low amplitude surface and low amplitude Moho relief.[25] Many are even found to have negative free air gravity anomaly, though evidence has shown that all of them should have experienced gravity high (positive free air gravity anomaly).[25] These have been suggested not caused by erosion and burial alone, as the adding of material into the basin would in fact increase the gravity strength rather than decrease it.[25] Thus viscous relaxation should have been taking place.[25] High heat flux and high water content in the early Martian crust favored viscous relaxation.[25] These two factors have made the crust more ductile. The basin topography of the craters would be subjected to greater stress due to self-gravitation. Such stress would drive crustal flow and therefore decay of relief. The giant impact basins are the exceptions that have not experienced viscous relaxation, as crustal thinning has made the crust too thin to sustain sub-solidus crustal flow.[5][25]

Low bulk crustal density

The most recent crustal density model RM1 developed in 2017 gives the bulk crustal density to be 2582 ± 209 kg m⁻³ for Mars,[9] which represents a global average value.[9] Lateral variation of the crustal density should exist.[9] For example, over the volcanic complexes, local density is expected to be as high as 3231 ± 95 kg m⁻³,[9] which matched the meteorite data and previous estimations. In addition, the density of the northern hemisphere is in general higher than that of the southern hemisphere,[9] which may imply that the latter is more porous than the former.

To achieve the bulk value, porosity could play an important role. If the mineral grain density is chosen to be 3100 kg m⁻³,[9] 10% to 23% porosity could give a 200 kg m⁻³ drop in the bulk density.[9] If the pore spaces are filled with water or ice, bulk density decrease is also expected.[9] A further drop in bulk density could be explained by increasing density with depth,[9] with the surface layer more porous than the deeper Mars, and the increase of density with depth also has geographical variation.[9]

Engineering and scientific applications

Areoid

See also: Geography of Mars § Zero elevation, and Mars § Geography

Further information: Vertical datum

The topography model MEDGRs was developed through range (distance) measurement done by MOLA 2 instrument and radio tracking data of the Mars Global Surveyor (MGS).[36] The highest point is located at the Olympus Mons while the deepest point is located within the Hellas Basin.[36](Brown-Red: Topography high; Green-Blue: Topography low) (Credit: NASA/JPL-Caltech)

The areoid represents the gravitational and rotational equipotential figure of Mars, analogous to the concept of geoid ("sea level") on Earth.[5][36][37] This has been set as the reference frame for developing the MOLA Mission Experiment Gridded Data Records (MEGDRs),[5][36] which is a global topography model. The topography model is important in mapping the geomorphological features and understanding different kinds of processes on Mars.

To derive the areoid, two parts of works are required. First, as gravity data is essential for identifying the position of the center of mass of the planet,[36] which is largely affected by the distribution of the mass of the interior, radio tracking data of spacecraft is necessary.[36] This was largely done by the Mars Global Surveyor (MGS).[5][36] Then, the MOLA 2 instrument aboard the MGS, which operates at 400-km elevation orbit, could measure the range (distance) between the spacecraft and the ground surface through counting the round-trip time of flight of the pulse from the instrument.[36] Combination of these two works allows the areoid as well as the MEGDRs to be constructed. Based on the above, the areoid has taken the radius as the mean radius of the planet at the equator as 3396 km.[5][36]

Surface landing

As there is a large distance between Mars and Earth, immediate command to the lander is almost impossible and the landing relies highly on its autonomous system. It has been recognized that to avoid failure, precise understanding of the gravity field of Mars is essential for the landing projects, so that offsetting factors and uncertainties of gravitational effects could be minimized, allowing for a smooth landing progress.[38][39] The first ever man-made object landing on Mars, the Mars 2 lander, crashed for an unknown reason. Since the surface environment of Mars is complex, composed of laterally varying morphological patterns, in order to avoid rock hazard the landing progress should be further assisted by employment of LIDAR on site in determining the exact landing position and other protective measures.[38][39]

References

1. Hirt, C.; Claessens, S.J.; Kuhn, M.; Featherstone, W.E. (2012). "Kilometer-resolution gravity field of Mars: MGM2011". Planetary and Space Science. 67 (1): 147–154. Bibcode:2012P&SS...67..147H. doi:10.1016/j.pss.2012.02.006. hdl:20.500.11937/32270.
2. Watts, A. B.; Bodine, J. H.; Ribe, N. M. (1980-02-07). "Observations of flexure and the geological evolution of the Pacific Ocean basin". Nature. 283 (5747): 532–537. Bibcode:1980Natur.283..532W. doi:10.1038/283532a0. ISSN 1476-4687.
3. Jeffreys, H. (1959). The Earth 4th ed., 420.
4. Runcorn, S. K. (1965). "Changes in the Convection Pattern in the Earth's Mantle and Continental Drift: Evidence for a Cold Origin of the Earth". Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. 258 (1088): 228–251. doi:10.1098/rsta.1965.0037. JSTOR 73348.
5. Neumann, G. A.; Zuber, M. T.; Wieczorek, M. A.; McGovern, P. J.; Lemoine, F. G.; Smith, D. E. (2004-08-01). "Crustal structure of Mars from gravity and topography". Journal of Geophysical Research: Planets. 109 (E8): E08002. Bibcode:2004JGRE..109.8002N. doi:10.1029/2004je002262. ISSN 2156-2202.
6. Kiefer, Walter S. (2004-05-30). "Gravity evidence for an extinct magma chamber beneath Syrtis Major, Mars: a look at the magmatic plumbing system". Earth and Planetary Science Letters. 222 (2): 349–361. Bibcode:2004E&PSL.222..349K. doi:10.1016/j.epsl.2004.03.009.
7. Marty, J.C.; Balmino, G.; Duron, J.; Rosenblatt, P.; Maistre, S. Le; Rivoldini, A.; Dehant, V.; Hoolst, T. Van (2009). "Martian gravity field model and its time variations from MGS and Odyssey data". Planetary and Space Science. 57 (3): 350–363. Bibcode:2009P&SS...57..350M. doi:10.1016/j.pss.2009.01.004.
8. Smith, David E.; Zuber, Maria T.; Torrence, Mark H.; Dunn, Peter J.; Neumann, Gregory A.; Lemoine, Frank G.; Fricke, Susan K. (2009-05-01). "Time variations of Mars' gravitational field and seasonal changes in the masses of the polar ice caps". Journal of Geophysical Research: Planets. 114 (E5): E05002. Bibcode:2009JGRE..114.5002S. doi:10.1029/2008je003267. hdl:1721.1/74244. ISSN 2156-2202.
9. Goossens, Sander; Sabaka, Terence J.; Genova, Antonio; Mazarico, Erwan; Nicholas, Joseph B.; Neumann, Gregory A. (2017-08-16). "Evidence for a low bulk crustal density for Mars from gravity and topography". Geophysical Research Letters. 44 (15): 2017GL074172. Bibcode:2017GeoRL..44.7686G. doi:10.1002/2017gl074172. ISSN 1944-8007. PMC 5619241. PMID 28966411.
10. "CODATA Value: Newtonian constant of gravitation". The NIST Reference on Constants, Units, and Uncertainty. US National Institute of Standards and Technology. June 2015. Retrieved 2017-12-14. "2014 CODATA recommended values"
11. Jacobson, R. A. (2008). Ephemerides of the Martian Satellites—MAR080. JPL IOM 343R–08–006.
12. Kaula, W. M. (1966-11-15). "Tests and combination of satellite determinations of the gravity field with gravimetry". Journal of Geophysical Research. 71 (22): 5303–5314. Bibcode:1966JGR....71.5303K. doi:10.1029/JZ071i022p05303. ISSN 2156-2202.
13. Genova, Antonio; Goossens, Sander; Lemoine, Frank G.; Mazarico, Erwan; Neumann, Gregory A.; Smith, David E.; Zuber, Maria T. (2016). "Seasonal and static gravity field of Mars from MGS, Mars Odyssey and MRO radio science". Icarus. 272: 228–245. Bibcode:2016Icar..272..228G. doi:10.1016/j.icarus.2016.02.050.
14. Lemoine, F. G.; Smith, D. E.; Rowlands, D. D.; Zuber, M. T.; Neumann, G. A.; Chinn, D. S.; Pavlis, D. E. (2001-10-25). "An improved solution of the gravity field of Mars (GMM-2B) from Mars Global Surveyor". Journal of Geophysical Research: Planets. 106 (E10): 23359–23376. Bibcode:2001JGR...10623359L. doi:10.1029/2000je001426. ISSN 2156-2202.
15. Sinclair, A. T. (1971-12-01). "The Motions of the Satellites of Mars". Monthly Notices of the Royal Astronomical Society. 155 (2): 249–274. Bibcode:1971MNRAS.155..249S. doi:10.1093/mnras/155.2.249. ISSN 0035-8711.
16. Asmar, S. W.; Armstrong, J. W.; Iess, L.; Tortora, P. (2005-04-01). "Spacecraft Doppler tracking: Noise budget and accuracy achievable in precision radio science observations". Radio Science. 40 (2): RS2001. Bibcode:2005RaSc...40.2001A. doi:10.1029/2004RS003101. ISSN 1944-799X.
17. Mayor, Michel; Queloz, Didier (1995-11-23). "A Jupiter-mass companion to a solar-type star". Nature. 378 (6555): 355–359. Bibcode:1995Natur.378..355M. doi:10.1038/378355a0. ISSN 1476-4687.
18. Gapcynski, J. P.; Tolson, R. H.; Michael, W. H. (1977-09-30). "Mars gravity field: Combined Viking and Mariner 9 results". Journal of Geophysical Research. 82 (28): 4325–4327. Bibcode:1977JGR....82.4325G. doi:10.1029/js082i028p04325. ISSN 2156-2202.
19. Balmino, G.; Moynot, B.; Valès, N. (1982-01-01). "Gravity field model of mars in spherical harmonics up to degree and order eighteen". Journal of Geophysical Research: Solid Earth. 87 (B12): 9735–9746. Bibcode:1982JGR....87.9735B. doi:10.1029/jb087ib12p09735. ISSN 2156-2202.
20. Smith, D. E.; Lerch, F. J.; Nerem, R. S.; Zuber, M. T.; Patel, G. B.; Fricke, S. K.; Lemoine, F. G. (1993-11-25). "An improved gravity model for Mars: Goddard Mars model 1". Journal of Geophysical Research: Planets. 98 (E11): 20871–20889. Bibcode:1993JGR....9820871S. doi:10.1029/93JE01839. ISSN 2156-2202.
21. Konopliv, Alexander S; Sjogren, William L (February 1, 1995). "The JPL Mars gravity field, Mars50c, based upon Viking and Mariner 9 Doppler tracking data" – via NASA Technical Report Server. Cite journal requires |journal= (help)
22. Lemoine, F. G., 2009. NASA PDS. http://pdf-geosciences.wustl.edu/mro/mro-m-rss-5-sdp-v1/mrors_1xxx/data/shadr/ggmro_095a_sha.lbl.
23. Konopliv, Alex S.; Yoder, Charles F.; Standish, E. Myles; Yuan, Dah-Ning; Sjogren, William L. (2006). "A global solution for the Mars static and seasonal gravity, Mars orientation, Phobos and Deimos masses, and Mars ephemeris". Icarus. 182 (1): 23–50. Bibcode:2006Icar..182...23K. doi:10.1016/j.icarus.2005.12.025.
24. Konopliv, Alex S.; Asmar, Sami W.; Folkner, William M.; Karatekin, Özgür; Nunes, Daniel C.; Smrekar, Suzanne E.; Yoder, Charles F.; Zuber, Maria T. (2011). "Mars high resolution gravity fields from MRO, Mars seasonal gravity, and other dynamical parameters". Icarus. 211 (1): 401–428. Bibcode:2011Icar..211..401K. doi:10.1016/j.icarus.2010.10.004.
25. Mohit, P. Surdas; Phillips, Roger J. (2007-11-01). "Viscous relaxation on early Mars: A study of ancient impact basins". Geophysical Research Letters. 34 (21): L21204. Bibcode:2007GeoRL..3421204M. doi:10.1029/2007GL031252. ISSN 1944-8007.
26. Airy, G. B. (1855). "On the Computation of the Effect of the Attraction of Mountain-Masses, as Disturbing the Apparent Astronomical Latitude of Stations in Geodetic Surveys". Philosophical Transactions of the Royal Society of London. 145: 101–104. doi:10.1098/rstl.1855.0003. JSTOR 108511.
27. Beuthe, M.; Le Maistre, S.; Rosenblatt, P.; Pätzold, M.; Dehant, V. (2012-04-01). "Density and lithospheric thickness of the Tharsis Province from MEX MaRS and MRO gravity data". Journal of Geophysical Research: Planets. 117 (E4): E04002. Bibcode:2012JGRE..117.4002B. doi:10.1029/2011je003976. ISSN 2156-2202.
28. Runcorn, S. K. (1963). "Satellite gravity measurements and convection in the mantle". Nature. 200 (4907): 628–630. doi:10.1038/200628a0.
29. A B Watts; Daly, and S. F. (1981). "Long Wavelength Gravity and Topography Anomalies". Annual Review of Earth and Planetary Sciences. 9 (1): 415–448. Bibcode:1981AREPS...9..415W. doi:10.1146/annurev.ea.09.050181.002215.
30. McKenzie, Dan (1977-02-01). "Surface deformation, gravity anomalies and convection". Geophysical Journal of the Royal Astronomical Society. 48 (2): 211–238. Bibcode:1977GeoJ...48..211M. doi:10.1111/j.1365-246X.1977.tb01297.x. ISSN 1365-246X.
31. Yoder, C. F.; Konopliv, A. S.; Yuan, D. N.; Standish, E. M.; Folkner, W. M. (2003-04-11). "Fluid Core Size of Mars from Detection of the Solar Tide". Science. 300 (5617): 299–303. Bibcode:2003Sci...300..299Y. CiteSeerX 10.1.1.473.6377. doi:10.1126/science.1079645. ISSN 0036-8075. PMID 12624177.
32. Karatekin, Ö.; Van Hoolst, T.; Dehant, V. (2006-06-01). "Martian global-scale CO2 exchange from time-variable gravity measurements". Journal of Geophysical Research: Planets. 111 (E6): E06003. Bibcode:2006JGRE..111.6003K. doi:10.1029/2005je002591. ISSN 2156-2202.
33. Sohl, Frank; Spohn, Tilman (1997-01-25). "The interior structure of Mars: Implications from SNC meteorites". Journal of Geophysical Research: Planets. 102 (E1): 1613–1635. Bibcode:1997JGR...102.1613S. CiteSeerX 10.1.1.456.2309. doi:10.1029/96JE03419. ISSN 2156-2202.
34. Nimmo, F.; Stevenson, D. J. (2001-03-25). "Estimates of Martian crustal thickness from viscous relaxation of topography". Journal of Geophysical Research: Planets. 106 (E3): 5085–5098. Bibcode:2001JGR...106.5085N. doi:10.1029/2000JE001331. ISSN 2156-2202.
35. Wieczorek, Mark A.; Zuber, Maria T. (2004-01-01). "Thickness of the Martian crust: Improved constraints from geoid-to-topography ratios". Journal of Geophysical Research: Planets. 109 (E1): E01009. Bibcode:2004JGRE..109.1009W. doi:10.1029/2003JE002153. ISSN 2156-2202.
36. Smith, David E.; Zuber, Maria T.; Frey, Herbert V.; Garvin, James B.; Head, James W.; Muhleman, Duane O.; Pettengill, Gordon H.; Phillips, Roger J.; Solomon, Sean C. (2001-10-25). "Mars Orbiter Laser Altimeter: Experiment summary after the first year of global mapping of Mars". Journal of Geophysical Research: Planets. 106 (E10): 23689–23722. Bibcode:2001JGR...10623689S. doi:10.1029/2000je001364. ISSN 2156-2202.
37. Ardalan, A. A.; Karimi, R.; Grafarend, E. W. (2009). "A New Reference Equipotential Surface, and Reference Ellipsoid for the Planet Mars". Earth, Moon, and Planets. 106 (1): 1–13. doi:10.1007/s11038-009-9342-7. ISSN 0167-9295.
38. Balaram, J., Austin, R., Banerjee, P., Bentley, T., Henriquez, D., Martin, B., ... & Sohl, G. (2002). Dsends-a high-fidelity dynamics and spacecraft simulator for entry, descent and surface landing. In Aerospace Conference Proceedings, 2002. IEEE (Vol. 7, pp. 7–7). IEEE.
39. Braun, R. D.; Manning, R. M. (2007). "Mars Exploration Entry, Descent, and Landing Challenges". Journal of Spacecraft and Rockets. 44 (2): 310–323. Bibcode:2007JSpRo..44..310B. CiteSeerX 10.1.1.463.8773. doi:10.2514/1.25116.