Adventures Among the Toroids

Adventures Among the Toroids: A study of orientable polyhedra with regular faces is a book on toroidal polyhedra that have regular polygons as their faces. It was written, hand-lettered, and illustrated by mathematician Bonnie Stewart, and self-published under the imprint "Number One Tall Search Book" in 1970.[1][2] Stewart put out a second edition, again hand-lettered and self-published, in 1980.[3][4][5] Although out of print, the Basic Library List Committee of the Mathematical Association of America has recommended its inclusion in undergraduate mathematics libraries.[6]

Topics
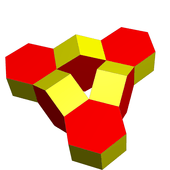
One of the Stewart toroids, formed as a ring of six hexagonal prisms

The Platonic solids, known to antiquity, have all faces regular polygons, all symmetric to each other (each face can be taken to each other face by a symmetry of the polyhedron). However, if less symmetry is required, a greater number of polyhedra can be formed while having all faces regular. The convex polyhedra with all faces regular were catalogued in 1966 by Norman Johnson (after earlier study e.g. by Martyn Cundy and A. P. Rollett), and have come to be known as the Johnson solids. Adventures Among the Toroids extends the investigation of polyhedra with regular faces to non-convex polyhedra, and in particular to polyhedra of higher genus than the sphere.[1][2][4] Many of these polyhedra can be formed by gluing together smaller polyhedral pieces, carving polyhedral tunnels through them, or piling them into elaborate towers.[4] The toroidal polyhedra described in this book, formed from regular polygons with no self-intersections or flat angles, have come to be called Stewart toroids.[7]

A ring of octahedra discussed in the second edition of the book

The second edition is rewritten in a different page format, letter sized in landscape mode compared to the tall and narrow 5 inches (13 cm) by 13 inches (33 cm) page size of the first edition,[5] with two columns per page.[3] It includes new material on knotted polyhedra and on rings of regular octahedra and regular dodecahedra; as the ring of dodecahedra forms the outline of a golden rhombus, it can be extended to make skeletal pentagon-faced versions of the convex polyhedra formed from the golden rhombus, including the Bilinski dodecahedron, rhombic icosahedron, and rhombic triacontahedron.[3] The second edition also includes the Császár polyhedron and Szilassi polyhedron, toroidal polyhedra with non-regular faces but with pairwise adjacent vertices and faces respectively, and constructions by Alaeglu and Giese of polyhedra with irregular but congruent faces and with the same numbers of edges at every vertex.[5]

Audience and reception

The second edition describes its intended audience in an elaborate subtitle, a throwback to times when long subtitles were more common: "a study of Quasi-Convex, aplanar, tunneled orientable polyhedra of positive genus having regular faces with disjoint interiors, being an elaborate description and instructions for the construction of an enormous number or new and fascinating mathematical models of interest to students of euclidean geometry and topology, both secondary and collegiate, to designers, engineers and architects, to the scientific audience concerned with molecular and other structural problems, and to mathematicians, both professional and dilletante, with hundreds of exercises and search projects, many outlined for self-instruction".[4]

Reviewer H. S. M. Coxeter summarizes the book as "a remarkable combination of sound mathematics, art, instruction and humor",[1] while Henry Crapo calls it "highly recommended" to others interested in polyhedra and their juxtapositions.[4]

Mathematician Joseph A. Troccolo calls a method of constructing physical models of polyhedra developed in the book, using cardboard and rubber bands, "of inestimable value in the classroom".[8] One virtue of this technique is that it allows for the quick disassembly and reuse of its parts.[9]

gollark: 320 doesn't really add anything much.
gollark: I see. Why not 256?
gollark: <@201731509223292928> What would this "reverse sigmoid function" be used for? I am interested in new control mechanisms.
gollark: Just simulate the universe up to when you think you remembered.
gollark: Instead of strictly a range.

References
  1. Coxeter, H. S. M., "Review of Adventures Among the Toroids (1st ed.)", Mathematical Reviews, MR 0275266
  2. "Review of Adventures Among the Toroids (1st ed.)", zbMATH (in German), Zbl 0214.47703
  3. Coxeter, H. S. M. (1982), "Review of Adventures Among the Toroids (2nd ed.)", Mathematical Reviews, MR 0588511
  4. Crapo, Henry (1980), "Review of Adventures Among the Toroids (2nd ed.)" (PDF), Structural Topology, 5: 45–48
  5. "Review of Adventures Among the Toroids (2nd ed.)", zbMATH, Zbl 0443.52005
  6. "Adventures Among the Toroids (unreviewed listing)", MAA Reviews, Mathematical Association of America, retrieved 2020-08-01
  7. Webb, Robert (2000), "Stella: Polyhedron Navigator", Symmetry: Culture and Science, 11 (1–4): 231–268
  8. Troccolo, Joseph A. (March 1976), "The algebra and geometry of polyhedra", The Mathematics Teacher, 69 (3): 220–224, JSTOR 27960432
  9. Prichett, Gordon D. (January 1976), "Three-dimensional discovery", The Mathematics Teacher, 69 (1): 5–10, JSTOR 27960351
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.