2-satisfiability
In computer science, 2-satisfiability, 2-SAT or just 2SAT is a computational problem of assigning values to variables, each of which has two possible values, in order to satisfy a system of constraints on pairs of variables. It is a special case of the general Boolean satisfiability problem, which can involve constraints on more than two variables, and of constraint satisfaction problems, which can allow more than two choices for the value of each variable. But in contrast to those more general problems, which are NP-complete, 2-satisfiability can be solved in polynomial time.
Instances of the 2-satisfiability problem are typically expressed as Boolean formulas of a special type, called conjunctive normal form (2-CNF) or Krom formulas. Alternatively, they may be expressed as a special type of directed graph, the implication graph, which expresses the variables of an instance and their negations as vertices in a graph, and constraints on pairs of variables as directed edges. Both of these kinds of inputs may be solved in linear time, either by a method based on backtracking or by using the strongly connected components of the implication graph. Resolution, a method for combining pairs of constraints to make additional valid constraints, also leads to a polynomial time solution. The 2-satisfiability problems provide one of two major subclasses of the conjunctive normal form formulas that can be solved in polynomial time; the other of the two subclasses is Horn-satisfiability.
2-satisfiability may be applied to geometry and visualization problems in which a collection of objects each have two potential locations and the goal is to find a placement for each object that avoids overlaps with other objects. Other applications include clustering data to minimize the sum of the diameters of the clusters, classroom and sports scheduling, and recovering shapes from information about their cross-sections.
In computational complexity theory, 2-satisfiability provides an example of an NL-complete problem, one that can be solved non-deterministically using a logarithmic amount of storage and that is among the hardest of the problems solvable in this resource bound. The set of all solutions to a 2-satisfiability instance can be given the structure of a median graph, but counting these solutions is #P-complete and therefore not expected to have a polynomial-time solution. Random instances undergo a sharp phase transition from solvable to unsolvable instances as the ratio of constraints to variables increases past 1, a phenomenon conjectured but unproven for more complicated forms of the satisfiability problem. A computationally difficult variation of 2-satisfiability, finding a truth assignment that maximizes the number of satisfied constraints, has an approximation algorithm whose optimality depends on the unique games conjecture, and another difficult variation, finding a satisfying assignment minimizing the number of true variables, is an important test case for parameterized complexity.
Problem representations
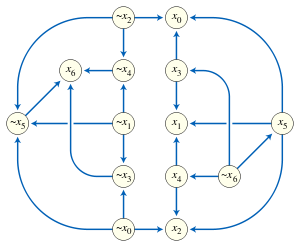
A 2-satisfiability problem may be described using a Boolean expression with a special restricted form. It is a conjunction (a Boolean and operation) of clauses, where each clause is a disjunction (a Boolean or operation) of two variables or negated variables. The variables or their negations appearing in this formula are known as literals.[1] For example, the following formula is in conjunctive normal form, with seven variables, eleven clauses, and 22 literals:
The 2-satisfiability problem is to find a truth assignment to these variables that makes the whole formula true. Such an assignment chooses whether to make each of the variables true or false, so that at least one literal in every clause becomes true. For the expression shown above, one possible satisfying assignment is the one that sets all seven of the variables to true. Every clause has at least one non-negated variable, so this assignment satisfies every clause. There are also 15 other ways of setting all the variables so that the formula becomes true. Therefore, the 2-satisfiability instance represented by this expression is satisfiable.
Formulas in this form are known as 2-CNF formulas. The "2" in this name stands for the number of literals per clause, and "CNF" stands for conjunctive normal form, a type of Boolean expression in the form of a conjunction of disjunctions.[1] They are also called Krom formulas, after the work of UC Davis mathematician Melven R. Krom, whose 1967 paper was one of the earliest works on the 2-satisfiability problem.[2]
Each clause in a 2-CNF formula is logically equivalent to an implication from one variable or negated variable to the other. For example, the second clause in the example may be written in any of three equivalent ways:
Because of this equivalence between these different types of operation, a 2-satisfiability instance may also be written in implicative normal form, in which we replace each or clause in the conjunctive normal form by the two implications to which it is equivalent.[3]
A third, more graphical way of describing a 2-satisfiability instance is as an implication graph. An implication graph is a directed graph in which there is one vertex per variable or negated variable, and an edge connecting one vertex to another whenever the corresponding variables are related by an implication in the implicative normal form of the instance. An implication graph must be a skew-symmetric graph, meaning that it has a symmetry that takes each variable to its negation and reverses the orientations of all of the edges.[4]
Algorithms
Several algorithms are known for solving the 2-satisfiability problem. The most efficient of them take linear time.[2][4][5]
Resolution and transitive closure
Krom (1967) described the following polynomial time decision procedure for solving 2-satisfiability instances.[2]
Suppose that a 2-satisfiability instance contains two clauses that both use the same variable x, but that x is negated in one clause and not in the other. Then the two clauses may be combined to produce a third clause, having the two other literals in the two clauses; this third clause must also be satisfied whenever the first two clauses are both satisfied. For instance, we may combine the clauses and in this way to produce the clause . In terms of the implicative form of a 2-CNF formula, this rule amounts to finding two implications and , and inferring by transitivity a third implication .[2]
Krom writes that a formula is consistent if repeated application of this inference rule cannot generate both the clauses and , for any variable . As he proves, a 2-CNF formula is satisfiable if and only if it is consistent. For, if a formula is not consistent, it is not possible to satisfy both of the two clauses and simultaneously. And, if it is consistent, then the formula can be extended by repeatedly adding one clause of the form or at a time, preserving consistency at each step, until it includes such a clause for every variable. At each of these extension steps, one of these two clauses may always be added while preserving consistency, for if not then the other clause could be generated using the inference rule. Once all variables have a clause of this form in the formula, a satisfying assignment of all of the variables may be generated by setting a variable to true if the formula contains the clause and setting it to false if the formula contains the clause .[2]
Krom was concerned primarily with completeness of systems of inference rules, rather than with the efficiency of algorithms. However, his method leads to a polynomial time bound for solving 2-satisfiability problems. By grouping together all of the clauses that use the same variable, and applying the inference rule to each pair of clauses, it is possible to find all inferences that are possible from a given 2-CNF instance, and to test whether it is consistent, in total time O(n3), where n is the number of variables in the instance. This formula comes from multiplying the number of variables by the O(n2) number of pairs of clauses involving a given variable, to which the inference rule may be applied. Thus, it is possible to determine whether a given 2-CNF instance is satisfiable in time O(n3). Because finding a satisfying assignment using Krom's method involves a sequence of O(n) consistency checks, it would take time O(n4). Even, Itai & Shamir (1976) quote a faster time bound of O(n2) for this algorithm, based on more careful ordering of its operations. Nevertheless, even this smaller time bound was greatly improved by the later linear time algorithms of Even, Itai & Shamir (1976) and Aspvall, Plass & Tarjan (1979).
In terms of the implication graph of the 2-satisfiability instance, Krom's inference rule can be interpreted as constructing the transitive closure of the graph. As Cook (1971) observes, it can also be seen as an instance of the Davis–Putnam algorithm for solving satisfiability problems using the principle of resolution. Its correctness follows from the more general correctness of the Davis–Putnam algorithm. Its polynomial time bound follows from the fact that each resolution step increases the number of clauses in the instance, which is upper bounded by a quadratic function of the number of variables.[6]
Limited backtracking
Even, Itai & Shamir (1976) describe a technique involving limited backtracking for solving constraint satisfaction problems with binary variables and pairwise constraints. They apply this technique to a problem of classroom scheduling, but they also observe that it applies to other problems including 2-SAT.[5]
The basic idea of their approach is to build a partial truth assignment, one variable at a time. Certain steps of the algorithms are "choice points", points at which a variable can be given either of two different truth values, and later steps in the algorithm may cause it to backtrack to one of these choice points. However, only the most recent choice can be backtracked over. All choices made earlier than the most recent one are permanent.[5]
Initially, there is no choice point, and all variables are unassigned. At each step, the algorithm chooses the variable whose value to set, as follows:
- If there is a clause both of whose variables are already set, in a way that falsifies the clause, then the algorithm backtracks to its most recent choice point, undoing the assignments it made since that choice, and reverses the decision made at that choice. If there is no choice point, or if the algorithm has already backtracked over the most recent choice point, then it aborts the search and reports that the input 2-CNF formula is unsatisfiable.
- If there is a clause in which one of the clause's two variables has already been set, and the clause could still become either true or false, then the other variable is set in a way that forces the clause to become true.
- In the remaining case, each clause is either guaranteed to become true no matter how the remaining variables are assigned, or neither of its two variables has been assigned yet. In this case the algorithm creates a new choice point and sets any one of the unassigned variables to an arbitrarily chosen value.
Intuitively, the algorithm follows all chains of inference after making each of its choices. This either leads to a contradiction and a backtracking step, or, if no contradiction is derived, it follows that the choice was a correct one that leads to a satisfying assignment. Therefore, the algorithm either correctly finds a satisfying assignment or it correctly determines that the input is unsatisfiable.[5]
Even et al. did not describe in detail how to implement this algorithm efficiently. They state only that by "using appropriate data structures in order to find the implications of any decision", each step of the algorithm (other than the backtracking) can be performed quickly. However, some inputs may cause the algorithm to backtrack many times, each time performing many steps before backtracking, so its overall complexity may be nonlinear. To avoid this problem, they modify the algorithm so that, after reaching each choice point, it begins simultaneously testing both of the two assignments for the variable set at the choice point, spending equal numbers of steps on each of the two assignments. As soon as the test for one of these two assignments would create another choice point, the other test is stopped, so that at any stage of the algorithm there are only two branches of the backtracking tree that are still being tested. In this way, the total time spent performing the two tests for any variable is proportional to the number of variables and clauses of the input formula whose values are permanently assigned. As a result, the algorithm takes linear time in total.[5]
Strongly connected components
Aspvall, Plass & Tarjan (1979) found a simpler linear time procedure for solving 2-satisfiability instances, based on the notion of strongly connected components from graph theory.[4]
Two vertices in a directed graph are said to be strongly connected to each other if there is a directed path from one to the other and vice versa. This is an equivalence relation, and the vertices of the graph may be partitioned into strongly connected components, subsets within which every two vertices are strongly connected. There are several efficient linear time algorithms for finding the strongly connected components of a graph, based on depth first search: Tarjan's strongly connected components algorithm[7] and the path-based strong component algorithm[8] each perform a single depth first search. Kosaraju's algorithm performs two depth first searches, but is very simple.
In terms of the implication graph, two literals belong to the same strongly connected component whenever there exist chains of implications from one literal to the other and vice versa. Therefore, the two literals must have the same value in any satisfying assignment to the given 2-satisfiability instance. In particular, if a variable and its negation both belong to the same strongly connected component, the instance cannot be satisfied, because it is impossible to assign both of these literals the same value. As Aspvall et al. showed, this is a necessary and sufficient condition: a 2-CNF formula is satisfiable if and only if there is no variable that belongs to the same strongly connected component as its negation.[4]
This immediately leads to a linear time algorithm for testing satisfiability of 2-CNF formulae: simply perform a strong connectivity analysis on the implication graph and check that each variable and its negation belong to different components. However, as Aspvall et al. also showed, it also leads to a linear time algorithm for finding a satisfying assignment, when one exists. Their algorithm performs the following steps:
- Construct the implication graph of the instance, and find its strongly connected components using any of the known linear-time algorithms for strong connectivity analysis.
- Check whether any strongly connected component contains both a variable and its negation. If so, report that the instance is not satisfiable and halt.
- Construct the condensation of the implication graph, a smaller graph that has one vertex for each strongly connected component, and an edge from component i to component j whenever the implication graph contains an edge uv such that u belongs to component i and v belongs to component j. The condensation is automatically a directed acyclic graph and, like the implication graph from which it was formed, it is skew-symmetric.
- Topologically order the vertices of the condensation. In practice this may be efficiently achieved as a side effect of the previous step, as components are generated by Kosaraju's algorithm in topological order and by Tarjan's algorithm in reverse topological order.[9]
- For each component in the reverse topological order, if its variables do not already have truth assignments, set all the literals in the component to be true. This also causes all of the literals in the complementary component to be set to false.
Due to the reverse topological ordering and the skew-symmetry, when a literal is set to true, all literals that can be reached from it via a chain of implications will already have been set to true. Symmetrically, when a literal x is set to false, all literals that lead to it via a chain of implications will themselves already have been set to false. Therefore, the truth assignment constructed by this procedure satisfies the given formula, which also completes the proof of correctness of the necessary and sufficient condition identified by Aspvall et al.[4]
As Aspvall et al. show, a similar procedure involving topologically ordering the strongly connected components of the implication graph may also be used to evaluate fully quantified Boolean formulae in which the formula being quantified is a 2-CNF formula.[4]
Applications
Conflict-free placement of geometric objects
A number of exact and approximate algorithms for the automatic label placement problem are based on 2-satisfiability. This problem concerns placing textual labels on the features of a diagram or map. Typically, the set of possible locations for each label is highly constrained, not only by the map itself (each label must be near the feature it labels, and must not obscure other features), but by each other: every two labels should avoid overlapping each other, for otherwise they would become illegible. In general, finding a label placement that obeys these constraints is an NP-hard problem. However, if each feature has only two possible locations for its label (say, extending to the left and to the right of the feature) then label placement may be solved in polynomial time. For, in this case, one may create a 2-satisfiability instance that has a variable for each label and that has a clause for each pair of labels that could overlap, preventing them from being assigned overlapping positions. If the labels are all congruent rectangles, the corresponding 2-satisfiability instance can be shown to have only linearly many constraints, leading to near-linear time algorithms for finding a labeling.[10] Poon, Zhu & Chin (1998) describe a map labeling problem in which each label is a rectangle that may be placed in one of three positions with respect to a line segment that it labels: it may have the segment as one of its sides, or it may be centered on the segment. They represent these three positions using two binary variables in such a way that, again, testing the existence of a valid labeling becomes a 2-satisfiability problem.[11]
Formann & Wagner (1991) use 2-satisfiability as part of an approximation algorithm for the problem of finding square labels of the largest possible size for a given set of points, with the constraint that each label has one of its corners on the point that it labels. To find a labeling with a given size, they eliminate squares that, if doubled, would overlap another point, and they eliminate points that can be labeled in a way that cannot possibly overlap with another point's label. They show that these elimination rules cause the remaining points to have only two possible label placements per point, allowing a valid label placement (if one exists) to be found as the solution to a 2-satisfiability instance. By searching for the largest label size that leads to a solvable 2-satisfiability instance, they find a valid label placement whose labels are at least half as large as the optimal solution. That is, the approximation ratio of their algorithm is at most two.[10][12] Similarly, if each label is rectangular and must be placed in such a way that the point it labels is somewhere along its bottom edge, then using 2-satisfiability to find the largest label size for which there is a solution in which each label has the point on a bottom corner leads to an approximation ratio of at most two.[13]
Similar applications of 2-satisfiability have been made for other geometric placement problems. In graph drawing, if the vertex locations are fixed and each edge must be drawn as a circular arc with one of two possible locations (for instance as an arc diagram), then the problem of choosing which arc to use for each edge in order to avoid crossings is a 2-satisfiability problem with a variable for each edge and a constraint for each pair of placements that would lead to a crossing. However, in this case it is possible to speed up the solution, compared to an algorithm that builds and then searches an explicit representation of the implication graph, by searching the graph implicitly.[14] In VLSI integrated circuit design, if a collection of modules must be connected by wires that can each bend at most once, then again there are two possible routes for the wires, and the problem of choosing which of these two routes to use, in such a way that all wires can be routed in a single layer of the circuit, can be solved as a 2-satisfiability instance.[15]
Boros et al. (1999) consider another VLSI design problem: the question of whether or not to mirror-reverse each module in a circuit design. This mirror reversal leaves the module's operations unchanged, but it changes the order of the points at which the input and output signals of the module connect to it, possibly changing how well the module fits into the rest of the design. Boros et al. consider a simplified version of the problem in which the modules have already been placed along a single linear channel, in which the wires between modules must be routed, and there is a fixed bound on the density of the channel (the maximum number of signals that must pass through any cross-section of the channel). They observe that this version of the problem may be solved as a 2-satisfiability instance, in which the constraints relate the orientations of pairs of modules that are directly across the channel from each other. As a consequence, the optimal density may also be calculated efficiently, by performing a binary search in which each step involves the solution of a 2-satisfiability instance.[16]
Data clustering
One way of clustering a set of data points in a metric space into two clusters is to choose the clusters in such a way as to minimize the sum of the diameters of the clusters, where the diameter of any single cluster is the largest distance between any two of its points. This is preferable to minimizing the maximum cluster size, which may lead to very similar points being assigned to different clusters. If the target diameters of the two clusters are known, a clustering that achieves those targets may be found by solving a 2-satisfiability instance. The instance has one variable per point, indicating whether that point belongs to the first cluster or the second cluster. Whenever any two points are too far apart from each other for both to belong to the same cluster, a clause is added to the instance that prevents this assignment.
The same method also can be used as a subroutine when the individual cluster diameters are unknown. To test whether a given sum of diameters can be achieved without knowing the individual cluster diameters, one may try all maximal pairs of target diameters that add up to at most the given sum, representing each pair of diameters as a 2-satisfiability instance and using a 2-satisfiability algorithm to determine whether that pair can be realized by a clustering. To find the optimal sum of diameters one may perform a binary search in which each step is a feasibility test of this type. The same approach also works to find clusterings that optimize other combinations than sums of the cluster diameters, and that use arbitrary dissimilarity numbers (rather than distances in a metric space) to measure the size of a cluster.[17] The time bound for this algorithm is dominated by the time to solve a sequence of 2-satisfiability instances that are closely related to each other, and Ramnath (2004) shows how to solve these related instances more quickly than if they were solved independently from each other, leading to a total time bound of O(n3) for the sum-of-diameters clustering problem.[18]
Scheduling
Even, Itai & Shamir (1976) consider a model of classroom scheduling in which a set of n teachers must be scheduled to teach each of m cohorts of students. The number of hours per week that teacher i spends with cohort j is described by entry Rij of a matrix R given as input to the problem, and each teacher also has a set of hours during which he or she is available to be scheduled. As they show, the problem is NP-complete, even when each teacher has at most three available hours, but it can be solved as an instance of 2-satisfiability when each teacher only has two available hours. (Teachers with only a single available hour may easily be eliminated from the problem.) In this problem, each variable vij corresponds to an hour that teacher i must spend with cohort j, the assignment to the variable specifies whether that hour is the first or the second of the teacher's available hours, and there is a 2-satisfiability clause preventing any conflict of either of two types: two cohorts assigned to a teacher at the same time as each other, or one cohort assigned to two teachers at the same time.[5]
Miyashiro & Matsui (2005) apply 2-satisfiability to a problem of sports scheduling, in which the pairings of a round-robin tournament have already been chosen and the games must be assigned to the teams' stadiums. In this problem, it is desirable to alternate home and away games to the extent possible, avoiding "breaks" in which a team plays two home games in a row or two away games in a row. At most two teams can avoid breaks entirely, alternating between home and away games; no other team can have the same home-away schedule as these two, because then it would be unable to play the team with which it had the same schedule. Therefore, an optimal schedule has two breakless teams and a single break for every other team. Once one of the breakless teams is chosen, one can set up a 2-satisfiability problem in which each variable represents the home-away assignment for a single team in a single game, and the constraints enforce the properties that any two teams have a consistent assignment for their games, that each team have at most one break before and at most one break after the game with the breakless team, and that no team has two breaks. Therefore, testing whether a schedule admits a solution with the optimal number of breaks can be done by solving a linear number of 2-satisfiability problems, one for each choice of the breakless team. A similar technique also allows finding schedules in which every team has a single break, and maximizing rather than minimizing the number of breaks (to reduce the total mileage traveled by the teams).[19]
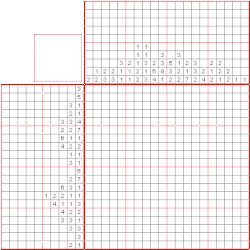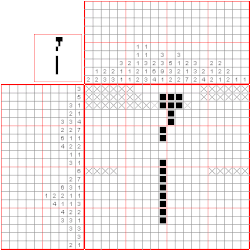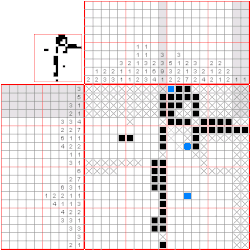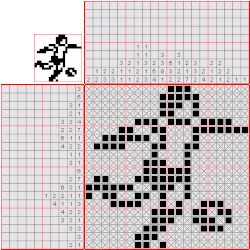
Discrete tomography
Tomography is the process of recovering shapes from their cross-sections. In discrete tomography, a simplified version of the problem that has been frequently studied, the shape to be recovered is a polyomino (a subset of the squares in the two-dimensional square lattice), and the cross-sections provide aggregate information about the sets of squares in individual rows and columns of the lattice. For instance, in the popular nonogram puzzles, also known as paint by numbers or griddlers, the set of squares to be determined represents the dark pixels in a binary image, and the input given to the puzzle solver tells him or her how many consecutive blocks of dark pixels to include in each row or column of the image, and how long each of those blocks should be. In other forms of digital tomography, even less information about each row or column is given: only the total number of squares, rather than the number and length of the blocks of squares. An equivalent version of the problem is that we must recover a given 0-1 matrix given only the sums of the values in each row and in each column of the matrix.
Although there exist polynomial time algorithms to find a matrix having given row and column sums,[20] the solution may be far from unique: any submatrix in the form of a 2 × 2 identity matrix can be complemented without affecting the correctness of the solution. Therefore, researchers have searched for constraints on the shape to be reconstructed that can be used to restrict the space of solutions. For instance, one might assume that the shape is connected; however, testing whether there exists a connected solution is NP-complete.[21] An even more constrained version that is easier to solve is that the shape is orthogonally convex: having a single contiguous block of squares in each row and column. Improving several previous solutions, Chrobak & Dürr (1999) showed how to reconstruct connected orthogonally convex shapes efficiently, using 2-SAT.[22] The idea of their solution is to guess the indexes of rows containing the leftmost and rightmost cells of the shape to be reconstructed, and then to set up a 2-satisfiability problem that tests whether there exists a shape consistent with these guesses and with the given row and column sums. They use four 2-satisfiability variables for each square that might be part of the given shape, one to indicate whether it belongs to each of four possible "corner regions" of the shape, and they use constraints that force these regions to be disjoint, to have the desired shapes, to form an overall shape with contiguous rows and columns, and to have the desired row and column sums. Their algorithm takes time O(m3n) where m is the smaller of the two dimensions of the input shape and n is the larger of the two dimensions. The same method was later extended to orthogonally convex shapes that might be connected only diagonally instead of requiring orthogonal connectivity.[23]
A part of a solver for full nonogram puzzles, Batenburg and Kosters (2008, 2009) used 2-satisfiability to combine information obtained from several other heuristics. Given a partial solution to the puzzle, they use dynamic programming within each row or column to determine whether the constraints of that row or column force any of its squares to be white or black, and whether any two squares in the same row or column can be connected by an implication relation. They also transform the nonogram into a digital tomography problem by replacing the sequence of block lengths in each row and column by its sum, and use a maximum flow formulation to determine whether this digital tomography problem combining all of the rows and columns has any squares whose state can be determined or pairs of squares that can be connected by an implication relation. If either of these two heuristics determines the value of one of the squares, it is included in the partial solution and the same calculations are repeated. However, if both heuristics fail to set any squares, the implications found by both of them are combined into a 2-satisfiability problem and a 2-satisfiability solver is used to find squares whose value is fixed by the problem, after which the procedure is again repeated. This procedure may or may not succeed in finding a solution, but it is guaranteed to run in polynomial time. Batenburg and Kosters report that, although most newspaper puzzles do not need its full power, both this procedure and a more powerful but slower procedure which combines this 2-satisfiability approach with the limited backtracking of Even, Itai & Shamir (1976)[5] are significantly more effective than the dynamic programming and flow heuristics without 2-satisfiability when applied to more difficult randomly generated nonograms.[24]
Renamable Horn satisfiability
Next to 2-satisfiability, the other major subclass of satisfiability problems that can be solved in polynomial time is Horn-satisfiability. In this class of satisfiability problems, the input is again a formula in conjunctive normal form. It can have arbitrarily many literals per clause but at most one positive literal. Lewis (1978) found a generalization of this class, renamable Horn satisfiability, that can still be solved in polynomial time by means of an auxiliary 2-satisfiability instance. A formula is renamable Horn when it is possible to put it into Horn form by replacing some variables by their negations. To do so, Lewis sets up a 2-satisfiability instance with one variable for each variable of the renamable Horn instance, where the 2-satisfiability variables indicate whether or not to negate the corresponding renamable Horn variables. In order to produce a Horn instance, no two variables that appear in the same clause of the renamable Horn instance should appear positively in that clause; this constraint on a pair of variables is a 2-satisfiability constraint. By finding a satisfying assignment to the resulting 2-satisfiability instance, Lewis shows how to turn any renamable Horn instance into a Horn instance in polynomial time.[25] By breaking up long clauses into multiple smaller clauses, and applying a linear-time 2-satisfiability algorithm, it is possible to reduce this to linear time.[26]
Other applications
2-satisfiability has also been applied to problems of recognizing undirected graphs that can be partitioned into an independent set and a small number of complete bipartite subgraphs,[27] inferring business relationships among autonomous subsystems of the internet,[28] and reconstruction of evolutionary trees.[29]
Complexity and extensions
NL-completeness
A nondeterministic algorithm for determining whether a 2-satisfiability instance is not satisfiable, using only a logarithmic amount of writable memory, is easy to describe: simply choose (nondeterministically) a variable v and search (nondeterministically) for a chain of implications leading from v to its negation and then back to v. If such a chain is found, the instance cannot be satisfiable. By the Immerman–Szelepcsényi theorem, it is also possible in nondeterministic logspace to verify that a satisfiable 2-satisfiability instance is satisfiable.
2-satisfiability is NL-complete,[30] meaning that it is one of the "hardest" or "most expressive" problems in the complexity class NL of problems solvable nondeterministically in logarithmic space. Completeness here means that a deterministic Turing machine using only logarithmic space can transform any other problem in NL into an equivalent 2-satisfiability problem. Analogously to similar results for the more well-known complexity class NP, this transformation together with the Immerman–Szelepcsényi theorem allow any problem in NL to be represented as a second order logic formula with a single existentially quantified predicate with clauses limited to length 2. Such formulae are known as SO-Krom.[31] Similarly, the implicative normal form can be expressed in first order logic with the addition of an operator for transitive closure.[31]
The set of all solutions
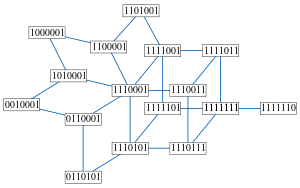
The set of all solutions to a 2-satisfiability instance has the structure of a median graph, in which an edge corresponds to the operation of flipping the values of a set of variables that are all constrained to be equal or unequal to each other. In particular, by following edges in this way one can get from any solution to any other solution. Conversely, any median graph can be represented as the set of solutions to a 2-satisfiability instance in this way. The median of any three solutions is formed by setting each variable to the value it holds in the majority of the three solutions. This median always forms another solution to the instance.[32]
Feder (1994) describes an algorithm for efficiently listing all solutions to a given 2-satisfiability instance, and for solving several related problems.[33] There also exist algorithms for finding two satisfying assignments that have the maximal Hamming distance from each other.[34]
Counting the number of satisfying assignments
#2SAT is the problem of counting the number of satisfying assignments to a given 2-CNF formula. This counting problem is #P-complete,[35] which implies that it is not solvable in polynomial time unless P = NP. Moreover, there is no fully polynomial randomized approximation scheme for #2SAT unless NP = RP and this even holds when the input is restricted to monotone 2-CNF formulas, i.e., 2-CNF formulas in which each literal is a positive occurrence of a variable.[36]
The fastest known algorithm for computing the exact number of satisfying assignments to a 2SAT formula runs in time .[37] [38] [39]
Random 2-satisfiability instances
One can form a 2-satisfiability instance at random, for a given number n of variables and m of clauses, by choosing each clause uniformly at random from the set of all possible two-variable clauses. When m is small relative to n, such an instance will likely be satisfiable, but larger values of m have smaller probabilities of being satisfiable. More precisely, if m/n is fixed as a constant α ≠ 1, the probability of satisfiability tends to a limit as n goes to infinity: if α < 1, the limit is one, while if α > 1, the limit is zero. Thus, the problem exhibits a phase transition at α = 1.[40]
Maximum-2-satisfiability
In the maximum-2-satisfiability problem (MAX-2-SAT), the input is a formula in conjunctive normal form with two literals per clause, and the task is to determine the maximum number of clauses that can be simultaneously satisfied by an assignment. Like the more general maximum satisfiability problem, MAX-2-SAT is NP-hard. The proof is by reduction from 3SAT.[41]
By formulating MAX-2-SAT as a problem of finding a cut (that is, a partition of the vertices into two subsets) maximizing the number of edges that have one endpoint in the first subset and one endpoint in the second, in a graph related to the implication graph, and applying semidefinite programming methods to this cut problem, it is possible to find in polynomial time an approximate solution that satisfies at least 0.940... times the optimal number of clauses.[42] A balanced MAX 2-SAT instance is an instance of MAX 2-SAT where every variable appears positively and negatively with equal weight. For this problem, Austrin has improved the approximation ratio to .[43]
If the unique games conjecture is true, then it is impossible to approximate MAX 2-SAT, balanced or not, with an approximation constant better than 0.943... in polynomial time.[44] Under the weaker assumption that P ≠ NP, the problem is only known to be inapproximable within a constant better than 21/22 = 0.95454...[45]
Various authors have also explored exponential worst-case time bounds for exact solution of MAX-2-SAT instances.[46]
Weighted-2-satisfiability
In the weighted 2-satisfiability problem (W2SAT), the input is an -variable 2SAT instance and an integer k, and the problem is to decide whether there exists a satisfying assignment in which at most k of the variables are true.
The W2SAT problem includes as a special case the vertex cover problem, of finding a set of k vertices that together touch all the edges of a given undirected graph. For any given instance of the vertex cover problem, one can construct an equivalent W2SAT problem with a variable for each vertex of a graph. Each edge uv of the graph may be represented by a 2SAT clause u ∨ v that can be satisfied only by including either u or v among the true variables of the solution. Then the satisfying instances of the resulting 2SAT formula encode solutions to the vertex cover problem, and there is a satisfying assignment with k true variables if and only if there is a vertex cover with k vertices. Therefore, like vertex cover, W2SAT is NP-complete.
Moreover, in parameterized complexity W2SAT provides a natural W[1]-complete problem,[47] which implies that W2SAT is not fixed-parameter tractable unless this holds for all problems in W[1]. That is, it is unlikely that there exists an algorithm for W2SAT whose running time takes the form f(k)·nO(1). Even more strongly, W2SAT cannot be solved in time no(k) unless the exponential time hypothesis fails.[48]
Quantified Boolean formulae
As well as finding the first polynomial-time algorithm for 2-satisfiability, Krom (1967) also formulated the problem of evaluating fully quantified Boolean formulae in which the formula being quantified is a 2-CNF formula. The 2-satisfiability problem is the special case of this quantified 2-CNF problem, in which all quantifiers are existential. Krom also developed an effective decision procedure for these formulae. Aspvall, Plass & Tarjan (1979) showed that it can be solved in linear time, by an extension of their technique of strongly connected components and topological ordering.[2][4]
Many-valued logics
The 2-satisfiability problem can also be asked for propositional many-valued logics. The algorithms are not usually linear, and for some logics the problem is even NP-complete. See Hähnle (2001, 2003) for surveys.[49]
References
- Prestwich, Steven (2009), "2. CNF Encodings", in Biere, Armin; Heule, Marijn; van Maaren, Hans; Walsh, Toby (eds.), Handbook of Satisfiability, Frontiers in Artificial Intelligence and Applications, 185, IOS Press, pp. 75–98, doi:10.3233/978-1-58603-929-5-75, ISBN 978-1-58603-929-5.
- Krom, Melven R. (1967), "The Decision Problem for a Class of First-Order Formulas in Which all Disjunctions are Binary", Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, 13 (1–2): 15–20, doi:10.1002/malq.19670130104.
- Russell, Stuart Jonathan; Norvig, Peter (2010), Artificial Intelligence: A Modern Approach, Prentice Hall series in artificial intelligence, Prentice Hall, p. 282, ISBN 978-0-13-604259-4.
- Aspvall, Bengt; Plass, Michael F.; Tarjan, Robert E. (1979), "A linear-time algorithm for testing the truth of certain quantified boolean formulas" (PDF), Information Processing Letters, 8 (3): 121–123, doi:10.1016/0020-0190(79)90002-4.
- Even, S.; Itai, A.; Shamir, A. (1976), "On the complexity of time table and multi-commodity flow problems", SIAM Journal on Computing, 5 (4): 691–703, doi:10.1137/0205048.
- Cook, Stephen A. (1971), "The complexity of theorem-proving procedures", Proc. 3rd ACM Symp. Theory of Computing (STOC), pp. 151–158, doi:10.1145/800157.805047.
- Tarjan, Robert E. (1972), "Depth-first search and linear graph algorithms", SIAM Journal on Computing, 1 (2): 146–160, doi:10.1137/0201010.
- First published by Cheriyan, J.; Mehlhorn, K. (1996), "Algorithms for dense graphs and networks on the random access computer", Algorithmica, 15 (6): 521–549, doi:10.1007/BF01940880. Rediscovered in 1999 by Harold N. Gabow, and published in Gabow, Harold N. (2003), "Searching (Ch 10.1)", in Gross, J. L.; Yellen, J. (eds.), Discrete Math. and its Applications: Handbook of Graph Theory, 25, CRC Press, pp. 953–984.
- Harrison, Paul, Robust topological sorting and Tarjan's algorithm in Python, retrieved 9 February 2011
- Formann, M.; Wagner, F. (1991), "A packing problem with applications to lettering of maps", Proc. 7th ACM Symposium on Computational Geometry, pp. 281–288, doi:10.1145/109648.109680, ISBN 978-0-89791-426-0.
- Poon, Chung Keung; Zhu, Binhai; Chin, Francis (1998), "A polynomial time solution for labeling a rectilinear map", Information Processing Letters, 65 (4): 201–207, doi:10.1016/S0020-0190(98)00002-7.
- Wagner, Frank; Wolff, Alexander (1997), "A practical map labeling algorithm", Computational Geometry: Theory and Applications, 7 (5–6): 387–404, doi:10.1016/S0925-7721(96)00007-7.
- Doddi, Srinivas; Marathe, Madhav V.; Mirzaian, Andy; Moret, Bernard M. E.; Zhu, Binhai (1997), "Map labeling and its generalizations", Proc. 8th ACM-SIAM Symp. Discrete Algorithms (SODA), Soda '97, pp. 148–157, ISBN 9780898713909.
- Efrat, Alon; Erten, Cesim; Kobourov, Stephen G. (2007), "Fixed-location circular arc drawing of planar graphs" (PDF), Journal of Graph Algorithms and Applications, 11 (1): 145–164, doi:10.7155/jgaa.00140.
- Raghavan, Raghunath; Cohoon, James; Sahni, Sartaj (1986), "Single bend wiring", Journal of Algorithms, 7 (2): 232–237, doi:10.1016/0196-6774(86)90006-4.
- Boros, Endre; Hammer, Peter Ladislaw; Minoux, Michel; Rader, David J., Jr. (1999), "Optimal cell flipping to minimize channel density in VLSI design and pseudo-Boolean optimization", Discrete Applied Mathematics, 90 (1–3): 69–88, doi:10.1016/S0166-218X(98)00114-0.
- Hansen, P.; Jaumard, B. (1987), "Minimum sum of diameters clustering", Journal of Classification, 4 (2): 215–226, doi:10.1007/BF01896987.
- Ramnath, Sarnath (2004), "Dynamic digraph connectivity hastens minimum sum-of-diameters clustering", SIAM Journal on Discrete Mathematics, 18 (2): 272–286, doi:10.1137/S0895480102396099.
- Miyashiro, Ryuhei; Matsui, Tomomi (2005), "A polynomial-time algorithm to find an equitable home–away assignment", Operations Research Letters, 33 (3): 235–241, CiteSeerX 10.1.1.64.240, doi:10.1016/j.orl.2004.06.004.
- Brualdi, R. A. (1980), "Matrices of zeros and ones with fixed row and column sum vectors", Linear Algebra Appl., 33: 159–231, doi:10.1016/0024-3795(80)90105-6.
- Woeginger, G. J. (1996), The reconstruction of polyominoes from their orthogonal projections, Technical Report SFB-65, Graz, Austria: TU Graz.
- Chrobak, Marek; Dürr, Christoph (1999), "Reconstructing hv-convex polyominoes from orthogonal projections", Information Processing Letters, 69 (6): 283–289, arXiv:cs/9906021, Bibcode:1999cs........6021D, doi:10.1016/S0020-0190(99)00025-3.
- Kuba, Attila; Balogh, Emese (2002), "Reconstruction of convex 2D discrete sets in polynomial time", Theoretical Computer Science, 283 (1): 223–242, doi:10.1016/S0304-3975(01)00080-9; Brunetti, Sara; Daurat, Alain (2003), "An algorithm reconstructing convex lattice sets" (PDF), Theoretical Computer Science, 304 (1–3): 35–57, doi:10.1016/S0304-3975(03)00050-1.
- Batenburg, K. Joost; Kosters, Walter A. (2008), "A reasoning framework for solving Nonograms", Combinatorial Image Analysis, 12th International Workshop, IWCIA 2008, Buffalo, NY, USA, April 7–9, 2008, Proceedings, Lecture Notes in Computer Science, 4958, Springer-Verlag, pp. 372–383, doi:10.1007/978-3-540-78275-9_33, ISBN 978-3-540-78274-2; Batenburg, K. Joost; Kosters, Walter A. (2009), "Solving Nonograms by combining relaxations", Pattern Recognition, 42 (8): 1672–1683, CiteSeerX 10.1.1.177.76, doi:10.1016/j.patcog.2008.12.003.
- Lewis, Harry R. (1978), "Renaming a set of clauses as a Horn set", Journal of the ACM, 25 (1): 134–135, doi:10.1145/322047.322059, MR 0468315.
- Aspvall, Bengt (1980), "Recognizing disguised NR(1) instances of the satisfiability problem", Journal of Algorithms, 1 (1): 97–103, doi:10.1016/0196-6774(80)90007-3, MR 0578079.
- Brandstädt, Andreas; Hammer, Peter Ladislaw; Le, Van Bang; Lozin, Vadim V. (2005), "Bisplit graphs", Discrete Mathematics, 299 (1–3): 11–32, doi:10.1016/j.disc.2004.08.046.
- Wang, Hao; Xie, Haiyong; Yang, Yang Richard; Silberschatz, Avi; Li, Li Erran; Liu, Yanbin (2005), "Stable egress route selection for interdomain traffic engineering: model and analysis", 13th IEEE Conf. Network Protocols (ICNP), pp. 16–29, CiteSeerX 10.1.1.106.7345, doi:10.1109/ICNP.2005.39, ISBN 978-0-7695-2437-5.
- Eskin, Eleazar; Halperin, Eran; Karp, Richard M. (2003), "Efficient reconstruction of haplotype structure via perfect phylogeny", Journal of Bioinformatics and Computational Biology, 1 (1): 1–20, doi:10.1142/S0219720003000174, PMID 15290779.
- Papadimitriou, Christos H. (1994), Computational Complexity, Addison-Wesley, pp. chapter 4.2, ISBN 978-0-201-53082-7., Thm. 16.3.
- Cook, Stephen; Kolokolova, Antonina (2004), "A Second-Order Theory for NL", 19th Annual IEEE Symposium on Logic in Computer Science (LICS'04), pp. 398–407, doi:10.1109/LICS.2004.1319634, ISBN 978-0-7695-2192-3.
- Bandelt, Hans-Jürgen; Chepoi, Victor (2008), "Metric graph theory and geometry: a survey", Surveys on discrete and computational geometry, Contemporary Mathematics, 453, Providence, RI: American Mathematical Society, pp. 49–86, doi:10.1090/conm/453/08795, ISBN 9780821842393, MR 2405677. Chung, F. R. K.; Graham, R. L.; Saks, M. E. (1989), "A dynamic location problem for graphs" (PDF), Combinatorica, 9 (2): 111–132, doi:10.1007/BF02124674. Feder, T. (1995), Stable Networks and Product Graphs, Memoirs of the American Mathematical Society, 555.
- Feder, Tomás (1994), "Network flow and 2-satisfiability", Algorithmica, 11 (3): 291–319, doi:10.1007/BF01240738.
- Angelsmark, Ola; Thapper, Johan (2005), "Algorithms for the maximum Hamming distance problem", Recent Advances in Constraints, Lecture Notes in Computer Science, 3419, Springer-Verlag, pp. 128–141, doi:10.1007/11402763_10, ISBN 978-3-540-25176-7.
- Valiant, Leslie G. (1979), "The complexity of enumeration and reliability problems", SIAM Journal on Computing, 8 (3): 410–421, doi:10.1137/0208032
- Welsh, Dominic; Gale, Amy (2001), "The complexity of counting problems", Aspects of complexity: minicourses in algorithmics, complexity and computational algebra: mathematics workshop, Kaikoura, January 7–15, 2000, pp. 115ff, Theorem 57.
- Dahllöf, Vilhelm; Jonsson, Peter; Wahlström, Magnus (2005), "Counting models for 2SAT and 3SAT formulae", Theoretical Computer Science, 332 (1–3): 265–291, doi:10.1016/j.tcs.2004.10.037
- Fürer, Martin; Kasiviswanathan, Shiva Prasad (2007), "Algorithms for counting 2-SAT solutions and colorings with applications", Algorithmic Aspects in Information and Management, Lecture Notes in Computer Science, 4508, Springer-Verlag, pp. 47–57, CiteSeerX 10.1.1.634.4498, doi:10.1007/978-3-540-72870-2_5, ISBN 978-3-540-72868-9.
- Wahlström, Magnus (2008), "A tighter bound for counting max-weight solutions to 2sat instances", International Workshop on Parameterized and Exact Computation, Lecture Notes in Computer Science, 5018, pp. 202–213, CiteSeerX 10.1.1.129.9232, doi:10.1007/978-3-540-79723-4_19, ISBN 978-3-540-79722-7
- Bollobás, Béla; Borgs, Christian; Chayes, Jennifer T.; Kim, Jeong Han; Wilson, David B. (2001), "The scaling window of the 2-SAT transition", Random Structures and Algorithms, 18 (3): 201–256, arXiv:math/9909031, doi:10.1002/rsa.1006; Chvátal, V.; Reed, B. (1992), "Mick gets some (the odds are on his side)", Proc. 33rd IEEE Symp. Foundations of Computer Science (FOCS), pp. 620–627, doi:10.1109/SFCS.1992.267789, ISBN 978-0-8186-2900-6; Goerdt, A. (1996), "A threshold for unsatisfiability", Journal of Computer and System Sciences, 53 (3): 469–486, doi:10.1006/jcss.1996.0081.
- M. R. Garey; D. S. Johnson; L. J. Stockmeyer (1976), "Some simplified NP-complete graph problems", Theoretical Computer Science, 1 (3): 237–267, doi:10.1016/0304-3975(76)90059-1, ISSN 0304-3975; see pp. 4–6
- Lewin, Michael; Livnar, Dror; Zwick, Uri (2002), "Improved Rounding Techniques for the MAX 2-SAT and MAX DI-CUT Problems", Proceedings of the 9th International IPCO Conference on Integer Programming and Combinatorial Optimization, Springer-Verlag, pp. 67–82, ISBN 978-3-540-43676-8
- Austrin, Per (2007), "Balanced Max 2-sat Might Not Be the Hardest", Proceedings of the Thirty-ninth Annual ACM Symposium on Theory of Computing (STOC '07), New York, NY, USA: ACM, pp. 189–197, doi:10.1145/1250790.1250818, ISBN 978-1-59593-631-8.
- Khot, Subhash; Kindler, Guy; Mossel, Elchanan; O'Donnell, Ryan (2004), "Optimal Inapproximability Results for MAX-CUT and Other 2-Variable CSPs?", FOCS '04: Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, IEEE, pp. 146–154, CiteSeerX 10.1.1.126.2295, doi:10.1109/FOCS.2004.49, ISBN 978-0-7695-2228-9
- Håstad, Johan (2001), "Some optimal inapproximability results", Journal of the ACM, 48 (4): 798–859, CiteSeerX 10.1.1.638.2808, doi:10.1145/502090.502098.
- Bansal, N.; Raman, V. (1999), "Upper bounds for MaxSat: further improved", in Aggarwal, A.; Pandu Rangan, C. (eds.), Proc. 10th Conf. Algorithms and Computation, ISAAC'99, Lecture Notes in Computer Science, 1741, Springer-Verlag, pp. 247–258; Gramm, Jens; Hirsch, Edward A.; Niedermeier, Rolf; Rossmanith, Peter (2003), "Worst-case upper bounds for MAX-2-SAT with an application to MAX-CUT", Discrete Applied Mathematics, 130 (2): 139–155, doi:10.1016/S0166-218X(02)00402-X; Kojevnikov, Arist; Kulikov, Alexander S. (2006), "A new approach to proving upper bounds for MAX-2-SAT", Proc. 17th ACM-SIAM Symp. Discrete Algorithms, pp. 11–17, doi:10.1145/1109557.1109559, ISBN 978-0-89871-605-4
- Flum, Jörg; Grohe, Martin (2006), Parameterized Complexity Theory, Springer, ISBN 978-3-540-29952-3
- Chen, Jianer; Huang, Xiuzhen; Kanj, Iyad A.; Xia, Ge (2006), "Strong computational lower bounds via parameterized complexity", Journal of Computer and System Sciences, 72 (8): 1346–1367, doi:10.1016/j.jcss.2006.04.007
- Hähnle, Reiner (2001), "Advanced many-valued logics", in Gabbay, Dov M.; Günthner, Franz (eds.), Handbook of Philosophical Logic, 2, Springer, pp. 297–395, doi:10.1007/978-94-017-0452-6_5, ISBN 978-94-017-0452-6 (see in particular p. 373); Hähnle, Reiner (2003), "Complexity of Many-valued Logics", in Fitting, Melvin; Orlowska, Ewa (eds.), Beyond two: theory and applications of multiple-valued logic, Studies in Fuzziness and Soft Computing, 114, Springer, pp. 211–233, doi:10.1007/978-3-7908-1769-0_9, ISBN 978-3-7908-1541-2