Implication graph

In mathematical logic, an implication graph is a skew-symmetric directed graph G = (V, E) composed of vertex set V and directed edge set E. Each vertex in V represents the truth status of a Boolean literal, and each directed edge from vertex u to vertex v represents the material implication "If the literal u is true then the literal v is also true". Implication graphs were originally used for analyzing complex Boolean expressions.

An implication graph representing the 2-satisfiability instance

Applications

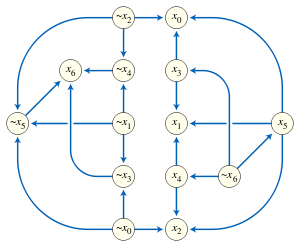
A 2-satisfiability instance in conjunctive normal form can be transformed into an implication graph by replacing each of its disjunctions by a pair of implications. For example, the statement can be rewritten as the pair . An instance is satisfiable if and only if no literal and its negation belong to the same strongly connected component of its implication graph; this characterization can be used to solve 2-satisfiability instances in linear time.[1]

In CDCL SAT-solvers, unit propagation can be naturally associated with an implication graph that captures all possible ways of deriving all implied literals from decision literals,[2] which is then used for clause learning.

gollark: jake is 68 insane, lemmmy is 109 insane.
gollark: I'm only 19 insane, I checked.
gollark: Why?
gollark: And are the *moderators* all the same, or 3 different people?
gollark: Wait, BTC is 3d6 too?

References
  1. Aspvall, Bengt; Plass, Michael F.; Tarjan, Robert E. (1979). "A linear-time algorithm for testing the truth of certain quantified boolean formulas". Information Processing Letters. 8 (3): 121–123. doi:10.1016/0020-0190(79)90002-4.
  2. Paul Beame; Henry Kautz; Ashish Sabharwal (2003). Understanding the Power of Clause Learning (PDF). IJCAI. pp. 1194–1201.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.