8

I have some fundamental questions on using Cryptographically Secure Pseudorandom Number Generators (CSPRNGs).

What should be the size of the seed that I initialize a CSPRNG with? How often should I reseed it? and how to determine the size of the reseeded entropy?

Any pointers will be helpful.

Mike Ounsworth
  • 57,707
  • 21
  • 150
  • 207
SkypeMeSM
  • 183
  • 7

2 Answers2

8

What matters is entropy.

What makes a PRNG cryptographically secure is the inability of attackers to predict the next bytes. Precisely, there are three "security levels" that define the security, in the following model:

  • The attacker is given s bits of consecutive output from the PRNG.
  • The attacker's computing abilities are limited to 2k elementary operations.
  • The attacker is challenged with predicting the next bit from the PRNG, and must not be able to succeed with probability greater than 0.5+2-e for some value e.

Note that predicting a bit can always be done with probability 0.5 (with a purely random guess), so what we require is that the attacker cannot do substantially better.

In all generality, we normally want the PRNG to fulfil these properties with k+e ≥ 128. The "128" is a traditional limit. Basically, the attacker will try to enumerate possible seed values, and see what matches the known output; if the attacker found the actual seed, then he can predict all subsequent output with 100% accuracy; otherwise, the attacker knows nothing and is back to luck-based guessing, i.e. probability 0.5 for each bit.

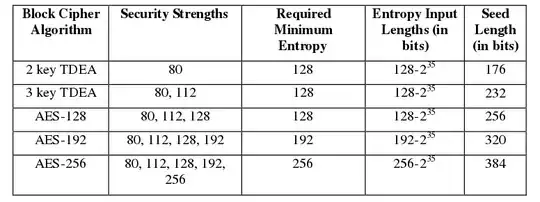
To achieve this level, the seed shall represent an entropy of at least 128 bits. In fact, stating that "seed S has entropy 128 bits" really means "attackers who try to guess S and do so by successive trials in optimal order, starting with the most probable values, will succeed after an average of 2127 trials". The term "average" is the important one here: entropy is all about probabilities and averages.

To have 128 bits of entropy, you need at least 128 bits of data, because you cannot fit n bits of entropy into less than n bits of data. However, real-life "random" data is extracted from physical measures, and is biased, so it needs more bits to be represented. For instance, you can get some randomness out of the timing of keypresses from the user: biologically speaking, the user cannot reproduce exact keypress timings down to the microsecond, so the delay between two keypresses, expressed in nanoseconds, will "contain" about 10 bits of entropy -- but a one-second delay requires 30 bits to be encoded in nanoseconds.

In general, as an application writer, you do not have to do the complex job of estimating entropy: the operating system already aggregates randomness from physical sources, and computes these estimates. When you ask the OS to give you "random bytes" (by opening /dev/urandom on Linux systems, or calling CryptGenRandom() on Windows), you already get bits that are clock-full of entropy. So ask for 128 bits (16 bytes) and you will have a fine enough seed for your PRNG.

(The "128" is traditional. Current technological limit for the richest of attackers is close to 275 operations, and unlikely to increase beyond 2100 in the next two or three decades. "128" is considered elegant by cryptographers because it is a power of 2.)

If your PRNG is really cryptographically secure, then reseeding is not needed -- a need to reseed would actually count as a break, thus contradicting with the notion of the PRNG being cryptographically secure.

Many people and standard still insist on reseeding, mostly because of an established dogma that says that you must reseed, for reasons which are never actually specified. This dogma comes from much older days, when PRNG were not cryptographically secure, and actually were not running on computers, because that was before computers were invented.

Thus, you should reseed as often as it takes to keep your auditors happy, but do not worry about the security issues of reseeding or not reseeding: you do not reseed to achieve more security, but to keep other people happy and quiet.

(If your CSPRNG is NOT cryptographically secure, reseeding is unlikely to save your skin anyway.)

Tom Leek
  • 168,808
  • 28
  • 337
  • 475
  • Thanks. I have a follow up question. Does that also mean that I can seed a CSPRNG only once, and use the same CSPRNG with all my cryptographic operations like generating keys, encryption etc. ? Or should I actually use multiple CSPRNGs for each operation and seed each CSPRNG once at initialization time? – SkypeMeSM Jul 22 '15 at 19:16
  • 1
    If your CSPRNG is really CS, you do not need to use several of them (if that was a problem, then your CSPRNG would not be really CS). – Tom Leek Jul 22 '15 at 19:20
  • 2
    If a PRNG is shared among different users, periodic reseeding will guard against the possibility that an earlier user may have discovered the then-current seed values through a side-channel attack (perhaps at a time when nobody else was using the system). Reseeding limits the value of the information such a user could gain. – supercat Jul 22 '15 at 22:04
  • 2
    If one could have a hardware CSPRNG which whose state was somehow invulnerable against compromise, such a device which was initialized from the factory with 128 bits of entry of which no other copy existed could from a practical perspective provide all the entropy anyone would ever need. If the state were compromised, however, so too would be all of the "entropy" it generated. – supercat Jul 22 '15 at 22:11
2

What should be the size of the seed that I initialize a CSPRNG with?

Seed Length and other requirements for approved block cipher algorithms are summarized here:

enter image description here

How often should I reseed it?

The seed is secure as long as it remains unknown to the attacker. I think I can not explain better than this answer.

CSPNRG entropy is calculated using the Min Entropy principle.

Community
  • 1