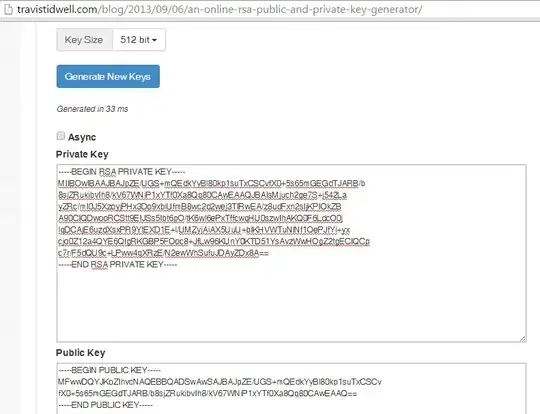
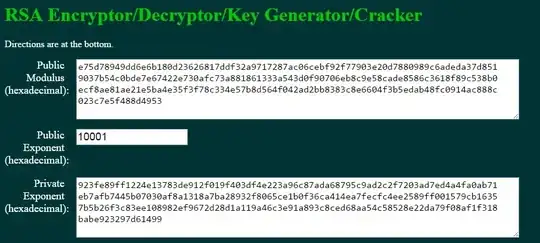
> I saw different key sizes for RSA algorithm (512, 1024,... [bits] for example) but, is this the length of public key or the length of private key or both are equal in length?
It's the length of the modulus used to compute the RSA key pair. The public key is made of modulus and public exponent, while the private key is made of modulus and private exponent.
> but the online tools for generating RSA key pairs have different lengths output!
The first picture shows public and private key in PEM format, encoded in Base64 (and not modulus and exponents of the key, which instead are shown in the second picture).
The content of the RSA private key is as follows:
-----BEGIN RSA PRIVATE KEY-----
RSAPrivateKey ::= SEQUENCE {
version Version,
modulus INTEGER, -- n
publicExponent INTEGER, -- e
privateExponent INTEGER, -- d
prime1 INTEGER, -- p
prime2 INTEGER, -- q
exponent1 INTEGER, -- d mod (p-1)
exponent2 INTEGER, -- d mod (q-1)
coefficient INTEGER, -- (inverse of q) mod p
otherPrimeInfos OtherPrimeInfos OPTIONAL
}
-----END RSA PRIVATE KEY-----
while a RSA public key contains only the following data:
-----BEGIN RSA PUBLIC KEY-----
RSAPublicKey ::= SEQUENCE {
modulus INTEGER, -- n
publicExponent INTEGER -- e
}
-----END RSA PUBLIC KEY-----
and this explains why the private key block is larger.
Now, why does the private key contain so much data? After all, only the modulus n and the private exponent d are needed. The reason all the other stuff is precomputed and included in the private key block is to speed up decryption using the Chinese Remainder Algorithm. (Kudos to @dbernard for pointing this out in the comments.)
Note that a more standard format for non-RSA public keys is
-----BEGIN PUBLIC KEY-----
PublicKeyInfo ::= SEQUENCE {
algorithm AlgorithmIdentifier,
PublicKey BIT STRING
}
AlgorithmIdentifier ::= SEQUENCE {
algorithm OBJECT IDENTIFIER,
parameters ANY DEFINED BY algorithm OPTIONAL
}
-----END PUBLIC KEY-----
More info here.
BTW, since you just posted a screenshot of the private key I strongly hope it was just for tests :)