Larger key sizes are said to be more difficult to bruteforce; is there any reason someone would then decide to instead use a smaller key?
Is there any negative effect in using a larger key size, such as performance, or poor compatibility with older versions of encryption/decryption software?
Each bit of a key increases the difficulty of a brute-force attack exponentially but there is a trade-off. Adding more bits to the key will negatively effect the speed of encryption/decryption. The actual amount of this speed loss depends on the algorithm, for example in RSA (in theory) for a n-bit key, computational effort for encryption is proportional to n^2, while effort for decryption is proportional to n^3, so doubling the key in RSA means that encryption will be four times slower, and decryption will be (almost) eight times slower.
Another thing I think is worth mentioning and thanks for Perseids for pointing it out. There is a limit where more time needed to break the algorithm becomes meaningless, because for practical purposes it is already "forever". As a "real world" analogy imagine you are packing rations for a short trip in the desert and are deciding how much water you want to take with you. For a small amount of water "more is better" is a reasonable approach, because you might need to stay longer than planned or spill some water. But when you already take the whole Amazon with you then increasing that amount to all the water on the planet does not help. That are the dimensions we are talking about when someone tries to convince you to use 8192 bit RSA.
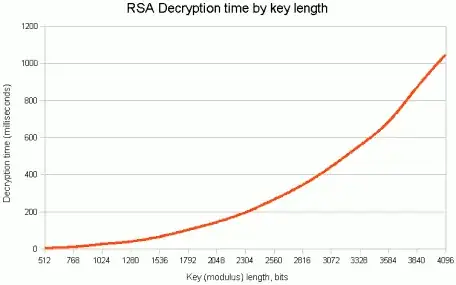
(Diagram from Javamex)
For elliptic curve algorithms, we assume that finding the discrete logarithm of a random elliptic curve element with respect to a publicly known base point is infeasible. The primary benefit of ECC is in fact the smaller key size e.g., a 256-bit ECC public key should provide comparable security to a 3072-bit RSA public key. Based on the fact that the main algorithms used to solve ECDLP (e.g baby-step giant-step) need n^(1/2) steps, increase/decrease in n-bits will affect de/encrption speeds.
As for your side question, I wouldn't worry too much but considering you are talking about length, "longer" is preferred.
There are several points to take into account:
"Key size" is not necessarily flexible. In symmetric encryption algorithms (e.g. AES), a key is "a bunch of bits" that must have a specific length. AES itself is not one algorithm but a family of three, who accept keys of, respectively, 128, 192 and 256 bits. No other key size will fit in.
Implementations can have limitations. If we consider RSA, whose keys are big integers (with some mathematical structure), the algorithm is in itself quite flexible, but implementations have constraints: some won't support keys longer than 2048 bits; some will require the key size to be "round" (e.g. multiple of 32). I work with smart cards who can do 1024-bit and 2048-bit RSA, but no other key size.
Costs rise with key size. CPU costs have been quoted in other answers; but size also matters: a 4096-bit RSA signature is twice longer than a 2048-bit RSA signature. We are talking network bandwidth here; this can matter more than CPU.
There are, or at least used to be, legal limitations for cryptographic key lengths (especially for export), depending on the country. This resulted in widely deployed implementations which cannot process keys beyond some size. For instance, some software can use AES-128 but not AES-256. Even when regulations are lifted, deployed software is not updated overnight.
Though people like to have bigger keys, it becomes meaningless at some point. We want keys which are "strong enough" to defeat any attacker who does not have extraterrestrial technology at his disposal. For symmetric encryption, this comes pretty fast: symmetric keys are bunch of n bits with no specific structure, so breaking such a key has average cost 2n-1 operations, so 128-bit keys are more than enough to be safe. For asymmetric encryption, attacks are not "brute force", but rather work on the mathematical structure of the key, which depends on the algorithm; for RSA, 2048 bits are (way) more than enough to defeat your adversaries (yeah, even the NSA / FSB / Illuminati or whoever your favourite nemesis is).
Growing keys beyond such values has thus no impact whatsoever on security (no positive impact, at least -- larger keys may imply decreased performance, thus incentive for users not to use them, which in turns decreases security). People who insist on 4096-bit RSA or AES-256 are misguided, or do that for other reasons (the other Bear would say that bigger keys are a courtship display for mating rituals, in the same category as red sports cars).
Practically speaking:
For symmetric encryption, you'll want AES-128. AES-256 is slightly less supported, and incurs a +40% CPU cost (that extra cost does not matter much usually, but it can happen).
For asymmetric encryption or signatures with RSA, go to 2048-bit keys. 1024-bit keys are not yet broken, but are theoretically within reach of human technology (entailing a special-purpose machine which has not been built yet because it would cost a lot more than even the richest universities care to spend). There are deployed implementations who cannot process keys larger than 2048 bits, and some cannot process key sizes between 1024 and 2048 either. 2048-bit keys thus maximize interoperability, and are fine for security.
With ECDSA or other algorithms with elliptic curves, the mathematical structure is different, so the figures are also different. A 256-bit EC key is as fine as AES-128, and, indeed, the NIST P-256 curve is the curve that is supported everywhere ECDSA is handled at all.
A recent Citrix Netscaler PR release points out that that the doubling of the key size from 1024-bit to 2048-bit increases CPU computational requirements from 4x to 8x.
(From a Network Computing article)
Larger/longer keys (I believe they're interchangeable) require more computational work - processor cycles - during use. Because keys are often used in asymmetric architectures (e.g., one web server for many web clients) the effect of the larger keys has a larger cumulative impact on the server, which in turn degrades performance and/or forces the server owner to throw more resources and money at the problem (larger server farm, SSL offloaders, etc. etc.)
Therefore, key sizes tend to be large enough to provide effective protection, but not larger.
The amount of available CPU resources in the typical end-user computers have gone down in the past five years, not up, due to the prevalence of mobile devices (smart phones and tablets). There is contention if the trend will be more or less resources for the average user, as less expensive products (i.e. E-ink readers) enter the market, but it is generally accepted the computationalloy-intensive software (such as Lastpass) should at least support the lower-CPU devices.
One consequence of this is key length and related computationally-expensive operations. As a single example, Lastpass recommends less Password Iterations (PBKDF2) for users who use mobile devices. I cannot find a web link, but when changing the Lastpass password in the in interface this is mentioned.
