I am a newbie to block cipher and when learning the CBC mode, I start to understand that an IV is being used in this mode and also will be transferred to the message receiver.
So here is my question, what if the IV is tampered? CBC mode can help to protect the integrity, but the IV is not encrypted, right?
If you look at the image down below, you can see how the Cipher Block Chaining Mode works for AES:
Source: Wikimedia Commons
For now, let's ignore all the other blocks of data, padding, etc., and just focus on the first block of data. The ciphertext is decrypted with the key, and then XOR'd with the IV.
Since the attacker can freely modify the IV, the changes to the IV are directly, bit-for-bit, reflected in the decrypted text. This property is called Malleability. In fact, all the blocks are malleable, since you can modify any block of choice and it'll be XOR'd into the result of the next block. Yes, you will "lose" one block, but depending on how the data is structured, that may be okay.
Yes, which is why AES-CBC must be used in combination with a primitive that guarantees integrity and authenticity. That means, if either the IV or the Ciphertext are modified, the decryption will fail.
Or, you can use Authenticated Encryption, such as AES-GCM, which will do all of this for you.
The answer above by @MechMK1 is spot on (+1).
Here's a working example of how IV malleability can be abused. Suppose that it's Super Bowl week, and there is a contest where the fee to enter is $10, but any participant that predicts the correct score of the game wins the entire pot. The organizer wants the contest to be transparent, so that all participants can verify the true and correct winner. But, the organizer also wants the predictions to be secret, so that none of the participants' predictions will influence the others. So the organizer instructs each participant to encrypt their prediction using AES-CBC, and send their encrypted prediction to all of the other participants before the game. Then, after the game, participants are to send the encryption key and IV that they used to encrypt their predictions to all of the participants, so that the predictions can be decrypted and revealed.
Bob, after reading @MechMK1's answer above, realizes that he can cheat, because the integrity of the IV is not being verified. By carefully crafting the encrypted message before the game, and carefully choosing an IV after the game, he can make the first block of decrypted plaintext whatever he wants, to make it look like he correctly predicted the score of the game.
He starts by crafting a plaintext message two blocks long, like so:
****************Superbowl LVI
where the *'s in the first block will eventually be replaced with his 'prediction'.
Then, he uses xxd to get the hexadecimal values of the underlying bytes that comprise the plaintext above:
echo -n '****************Superbowl LVI ' | xxd -p
This produces:
2a2a2a2a2a2a2a2a2a2a2a2a2a2a2a2a5375706572626f776c204c5649
Then, he chooses a random key (9ae3c94cbb1ea41d3678772a55a49189cd2deeba1dfa3b733e1674557a83cc7b) and a random iv (302775dfc35a35c8081bbc6fdeacbd86), and uses these to encrypt the plaintext with AES-CBC:
echo -n '2a2a2a2a2a2a2a2a2a2a2a2a2a2a2a2a5375706572626f776c204c5649' | xxd -p -r | openssl aes-256-cbc -e -K 9ae3c94cbb1ea41d3678772a55a49189cd2deeba1dfa3b733e1674557a83cc7b -iv 302775dfc35a35c8081bbc6fdeacbd86 | xxd -p
This produces the cipher text in hexadecimal format:
6408349083ef84e193aaebd35f735b5a08bc5f024dd623308f61e4582d2c18f6
He send this to the other participants.
Then, the game is played. The final score is LA 23, CIN 20.
Bob now goes about calculating the IV that he will need, such that the first block of decrypted plaintext will be:
'LA 23, CIN 20 - '
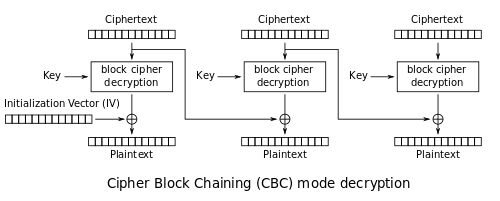
To do this, he looks at the CBC chaining diagram below, first focusing on the point labeled 'A':
Point A represents the first block, after it has been decrypted with AES using the key, but before it has been XOR'd with the IV. Because A xor 0 = A, Bob can see what the block at point A is, by decrypting the ciphertext using the key, and an IV of 00000000000000000000000000000000:
echo -n '6408349083ef84e193aaebd35f735b5a08bc5f024dd623308f61e4582d2c18f6' | xxd -p -r | openssl aes-256-cbc -d -K 9ae3c94cbb1ea41d3678772a55a49189cd2deeba1dfa3b733e1674557a83cc7b -iv 00000000000000000000000000000000 | xxd -p
This produces:
1a0d5ff5e9701fe222319645f48697ac5375706572626f776c204c5649
So, block at point A is:
1a0d5ff5e9701fe222319645f48697ac
Now, Bob can compute an IV (B), such that when the block at point (A) above is XOR'd with this IV, it produces his 'wanted plaintext' (C), which is: LA 23, CIN 20 - .
First he needs the hexadecimal values of the underlying bytes of his wanted plaintext:
echo -n 'LA 23, CIN 20 - ' | xxd -p
This produces:
4c412032332c2043494e203230202d20
So, the problem boils down to
A xor B = C
where A is 1a0d5ff5e9701fe222319645f48697ac and C is 4c412032332c2043494e203230202d20, and he needs to find B.
XOR is unique in that if you know any two of the three variables, you can easily find the third. That is:
A xor B = C
A xor C = B
B xor C = A
So, Bob uses the second equation above, and plugs in A and C, to calculate B. This can be done using python, like so:
python3 -c "print (hex(0x1a0d5ff5e9701fe222319645f48697ac ^ 0x4c412032332c2043494e203230202d20))"
This produces:
0x564c7fc7da5c3fa16b7fb677c4a6ba8c
So, the IV that produces Bob's wanted plaintext is: 564c7fc7da5c3fa16b7fb677c4a6ba8c.
Bob declares himself the winner. To prove it, he sends the key 9ae3c94cbb1ea41d3678772a55a49189cd2deeba1dfa3b733e1674557a83cc7b and the IV 564c7fc7da5c3fa16b7fb677c4a6ba8c to the other participants. They use these to decrypt the ciphertext that he sent them before the game, like so:
echo -n '6408349083ef84e193aaebd35f735b5a08bc5f024dd623308f61e4582d2c18f6' | xxd -p -r | openssl aes-256-cbc -d -K 9ae3c94cbb1ea41d3678772a55a49189cd2deeba1dfa3b733e1674557a83cc7b -iv 564c7fc7da5c3fa16b7fb677c4a6ba8c
And, lo and behold, this produces:
LA 23, CIN 20 - Superbowl LVI
