How are Mozilla Firefox passwords encrypted?

Question

As far as I know, current versions of Mozilla Firefox store the saved passwords (encrypted with 3DES) to the logins.json file meanwhile the keys are stored in key4.db (or key3.db in older versions).

If one hasn't set up a Master Key for the passwords, the key database file can then be accessed. In the database, I've encountered an entry that does indeed look like the keys.

------------------------------
|    id    | item1 | item2   |
------------------------------
| password |  ...  |  ...    |
------------------------------

So, why possibly are there two 3DES keys in the database? Are they really encryption keys? How can I use them to decrypt the logins.json data? Which keying option is being used?

I do not know all the details but the answers are contained in the code for this project to export Firefox passwords: https://github.com/louisabraham/ffpass — We Are All Monica, Aug 27 '19 at 04:42

score 7 · Answer 1 · edited Mar 25 '20 at 08:44

7

I have created a visual explanation of the firefox algorithm, not very pretty but I hope it helps.

edited Mar 25 '20 at 08:44

schroeder

123,438
55
284
319

answered Mar 25 '20 at 01:28

Ahsan Aziz

71
1
1

1

Can you summarise your diagram into something that answers the question? I see where 3DES is used, but not that different keys are used. Also, your script has nothing to do with the question. – schroeder Mar 25 '20 at 08:44
1

That's a nice diagram Ahsan! @schroeder I think it's actually very useful to have a simpler implementation than decades-old C code in a huge project, for those who want a deeper understanding of it and prefer to read the more readable Python. It doesn't have to be part of an answer to be nice material to link. – Luc Mar 25 '20 at 09:14
@luc yes, nice diagram. But it's not an *answer*. The diagram also only shows one 3DES key. – schroeder Mar 25 '20 at 09:16
@schroeder Are we talking about the diagram or about the code now? Because both answer the question in different ways, you have already deleted the code link and it sounds like you're thinking of deleting the whole answer. I agree a textual explanation to go with the diagram *should* be part of an answer, but by itself, the diagram also explains (albeit in very technical terms) how Firefox encrypts passwords. And there already is an answer with a textual overview, I'm not sure that needs duplicating (and as a comment on that answer, people wouldn't spot the nice diagram like they can now). – Luc Mar 25 '20 at 09:24
@Luc answers need to stand alone. The diagram by itself does not appear to answer the question at all (there is only one 3DES key), ***and*** it needs to be summarised. The code was just a link without context. This answer needs to relate to the question somehow. Dots need to be connected. – schroeder Mar 25 '20 at 09:31

A. Hersean · Accepted Answer · 2019-08-27T14:48:30.270

The comment by @jnylen gave a source for the algorithm.

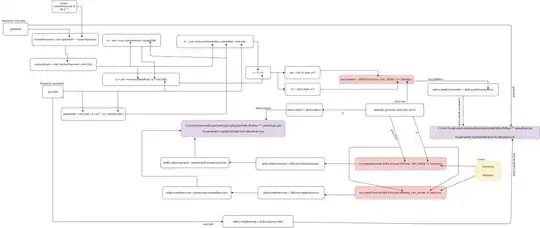
In the data structure, item1 is the global salt, and item2 contains (in DER encoding) the entry salt and the encrypted key. This key is used to encrypt the rest of the data (per username and password).

The encryption of the master key is done with 3DES-CBC, with a key (and IV) derived from the master password, a global salt and a "per entry" salt. By default, the master password is the empty string. The password's entropy is bounded to 160 bits by sha1, which is further bounded to 112 bits by 3DES. The password is not hardened using multiple iterations of an hash.

The encryption of items (usernames and passwords) is done using 3DES-CBC, with an IV included in the metadata of each item. How IV is generated cannot be guessed from this source of the algorithm.

Unless the IVs are poorly generated, the small amount of data encrypted means that the best attack on 3DES is brute-forcing the master key or the user's password. The upper bound of 112 bits means that is this algorithm is considered weak by today standards: a big organization with huge resources might be able to brute-force the key in a few decades. Quantum computers might break them faster.

In practice, this means that a good, long passphrase must be used as the master password. This algorithm is in need a good refactoring, moving to current best practices: Argon2id with at least 128MB and 3 iterations, and an AEAD cipher (like those used in TLS 1.3).

How are Mozilla Firefox passwords encrypted?

2 Answers2

Linked