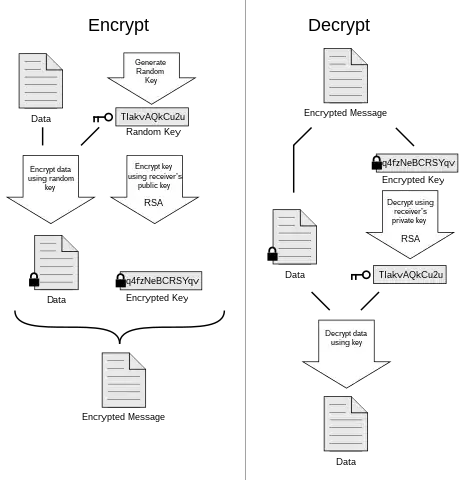
The ElGamal asymmetric encryption scheme can be adapted to elliptic curves (indeed, it works on any finite group for which discrete logarithm is hard). However, this means that the data to encrypt must be mapped to a curve point in a reversible manner, which is a bit tricky (that's doable but involves more mathematics, which means increased implementation code size). Since most of the time we use asymmetric encryption, we actually want to encrypt a session key which will be used for symmetric encryption, Diffie-Hellman key exchange on the elliptic curve is already fine, and simpler (that's what ECIES is: Diffie-Hellman then symmetric encryption).