AFAIK , When Alice wants to write a message to Bob -- she uses Bob's public key and encrypt the message - and then Bob - using his private key - use to decrypt it.
So public key is used to decrypt and private key is used to encrypt.
But then I saw this explanation ( in digital signature conext):
here it says that the hash value(signed) is encrypted with her private key ?
so private key uses not only for decryption(messages which sent to me) but also for encryption(hash which i calculate) ?
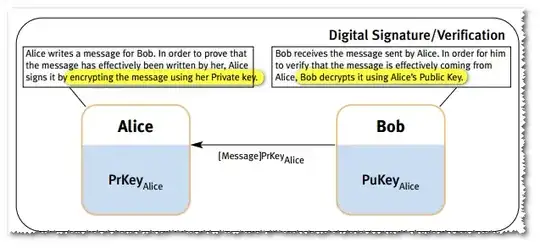
That's the usual confusion of "signing is like encrypting with your private key".
Just forget it. It is a terrible explanation which does not work. It just seemed to work in days of yore, when the very first digital signature algorithm (based on asymmetric cryptography) was first described (I am talking about RSA and it was in the Disco era); but even for RSA it is not correct since it fails to take into account padding, which is critical for security.
Have a look at PKCS#1 to see how RSA is used. In particular, when encrypting data with RSA and a 1024-bit key, the most you can encrypt in one go is 117 bytes, but the encryption result is always 128 bytes, and that's what a decryption engine expects. Regardless of how much you try, 128 bytes will not fit in less than 117 bytes...
What must be remembered is that a private key is what is used to do something that should not be doable by everybody. This means data decryption (anybody can encrypt a message to Bob, but only Bob should bee able to read it) and signature generation (everybody can verify a signature, but only Bob should be able to produce a signature that everybody can verify as being from Bob).
Although there are asymmetric encryption algorithms which can use the same kind of key as digital signature algorithms (there is RSA encryption and there is RSA signatures, and both use "RSA keys"), using the same key for both is not a good idea.
Asymmetric cryptography can be used to provide both confidentiality and authenticity.
In layman's terms, one can compute a cryptographic hash of a message and "encrypt" it with their private key, to produce a signature. Anyone who is in posession of the corresponding public key can use it to verify that the signature is correct. This allows us to prove that a message is authentic.
Conversely, it's possible to encrypt a message with the public key, and only the private key can decrypt it, even if everyone on the planet knows the public key. This allows us to make a message confidential.
When combined, these two properties allow us to communicate confidentially, and ensure that the person we're talking to really is the person we expect.
A private key is a factor of your public key. Through mathematics I don't really understand, anyone can encrypt you a message with your public key and only you can decrypt it with your private key. This is called RSA encryption for reference.
An important thing to note is RSA requires a longer key to be a effective as AES (symmetric encryption) and is used mostly for key distribution. The actual message will be encrypted with AES using a shared secret distributed over RSA.
