Occam's razor

Occam's razor is a logical razor which states that one should never make more assumptions than the minimum necessary to explain something; or, if you don't have explicit evidence to believe that something is true, then you should not. It is named after the 14^th-century English philosopher and theologian William of Ockam (or Occam or Ockham), born c. 1285. Died 1347/49.

Cogito ergo sum Logic and rhetoric

Key articles

Logical fallacy Syllogism Argument

General logic

Broken window fallacy Cherry picking Galileo gambit Implicit bias Lógica Relativist fallacy

Bad logic

Exception that proves the rule Fallacy of accent Gore's Law Mistaking the map for the territory Morton's fork Willful ignorance v - t - e

“”Plurality must never be posited without necessity.

—William of Ockam

“”So strange that people often believe things inversely proportionate to the evidence. Given a set of possible explanations, why pick the extremely unlikely one!?

—Elon Musk[1]

The mathematical proof by Ray Solomonoff that any sequence of observations is best predicted by Occam's Razor in a computable environment[2] (a.k.a. Solomonoff induction) should be considered in light of the fact that all mainstream physics models (such as the Standard Model) are computable. On the other hand, underground mind-controlling gerbiles might be biasing physicists into computability chauvinism so as to prevent humans from discovering the true laws of nature, which would lead them to the hoards of jewels and gold deep within the underground gerbie colonies. So those rational enough to be concerned with the possibility of underground mind-controlling gerbiles should consider Occam's Razor to be a "rule of thumb".

History

Although the principle bears his name, William of Ockam did not invent it. The concept is found in the writings of many other medieval philosophers, including Duns Scotus, Thomas Aquinas, and Durand de Saint-Pourcain, and has roots as far back as Aristotle. The medieval "rule of economy" that is, “plurality should not be assumed without necessity,” was then labeled “Ockham’s razor” because it was a powerful principle, used by Ockham to dispense with unnecessary assumptions, commonly used by scholastic philosophers. Thus making possible a scientific understanding of reality.[3] William of Ockam often expressed the principle as

“”Numquam ponenda est pluralitas sine necessitate. (A plurality [of causes] should never be posited unless necessary.

But the best known version is a paraphrase by the 17^th-century scholar John Ponce:

“”Entia non sunt multiplicanda praeter necessitatem. (Entities are not to be multiplied beyond what is necessary.)

In science

Its scientific application is to select priority between developing theories of equal predictive power. The "simpler" theory with fewer (or less onerous) assumptions is probably the most appropriate one. For example, if you see hoof-prints on your local walking trail, think horses, not Invisible Pink Unicorns.

Getting it right

Occam's razor is often misinterpreted.

In science Occam's razor evaluates only hypotheses with similar predictive power

Each hypothesis being evaluated must be able to predict the same final state. If a theory has no predictive power (such as Goddidit) then it is automatically excluded due to being impossible to evaluate.

Predictive power does not mean inclusive power

A theory which can include evidence is not the same as a theory which can predict results. The test of a theory comes from being able to generate results from base data or predict additional discoveries, not the power to use ad hoc reasoning to back-fit new data to the theory. A simple example would be fitting a polynomial of degree 399 to 400 data points: it might fit those 400 perfectly, but is the end behavior likely to be a good extrapolation or a really bad one?

A classic example of generating an excuse that creates infinite inclusive power (but not so much predictive power) is "The lord works in mysterious ways."

A theory must still be scientific

For the scientific use of Occam's razor to actually come into effect, a hypothesis must first satisfy the standard requirements of the scientific method; in particular, it must be falsifiable. Trying to use science to evaluate an unscientific theory is like trying to use metallurgy to evaluate a restaurant: forking stupid.

What is a "term?"

Often people use "term" as a synonym for "word" and imagine that the theory which can be described in the simplest way is selected by Occam's razor. This is not the case; one must carefully (and honestly) separate all assumptions being made.

For example, a simple-minded evaluation would say "my television functions because of electricity" is as "simple" as "my television functions because of Martians." But to actually evaluate these:

• 1. My television contains circuitry. 2. My television draws power from the mains which I can show is used by the circuitry. 3. The power from the mains going through the circuitry is what makes the television function.
• 1. My television contains circuitry. 2. My television draws power from the mains which I can show is used by the circuitry. 3. The power from the mains going through the circuitry is not what makes the television function. 4. It functions because of Martians. 5. Who are in orbit in their flying saucer. 6. Which is invisible and undetectable. 7. And powers my television in a way that is also invisible and undetectable. 8. And requires no obvious additional components in my television.

It should now be clear which of these would actually be regarded as containing the least number of additional terms. Also, the first hypothesis has predictive power: if you unplug the television from the mains, it ceases to function.

Naming an unknown

You cannot explain anything by simply replacing an unknown with an unknown which has a different name. If the hypothesis offers no clue how the result is reached, it is not simple, it is useless. For example:

1+X=2

It is not clear here whether X is a number, many numbers, or an operation of some kind. Based on this alone, the simplest explanation would be that X is 1. The Goddidit explanation would be

X=G

Where G is defined as "the correct answer". It should be fairly obvious that we have simply renamed the unknown, and know no more that we did to begin with about the unknown's identity.

Meaningful precision

One common question among people just beginning to learn high-level physics is "why learn Newtonian physics if they're wrong?" The answer provides a good example of the practical use of Occam's razor in selecting theories.

Let's say we have a one-metric ton car moving at 36 kilometres per hour, and we want to find out how much kinetic energy it has. Newton gives us the simple equation:

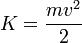
The car weights 1000 kilograms and is travelling at 10 metres per second, so we get an easy figure of 50,000 joules from a straightforward calculation. The Einsteinian method, hated by wiki markup the world over, includes relativistic change in mass, at the cost of performing various sorcery to get it. This gives us a value of 50,000.00000000004 joules.

"But isn't the Einsteinian working more accurate, then?" Those who understand mathematics probably recognise the fallacy here immediately, but for those who don't: the original measurements, in tons and kilometres per hour, simply don't have the precision needed to calculate a hundred-billionth of a joule, so the Einsteinian precision is actually an illusion.

Since the Einsteinian method imparts no meaningful additional level of accuracy, Occam's razor tells us to use the Newtonian method, because it gets the same result with far fewer terms, which is why the Newtonian physics equations are still used for most calculations involving macroscopic objects travelling at non-relativistic velocities.

Getting it wrong

Confusing the razor with knowledge division

Some confuse Occam's razor with a class of knowledge divisors that separate the empirical/falsifiable from the supernatural and pseudo-scientific (such as Popper's falsifiability theory) or even Hume's fork, which separate ideas and concepts from matters of fact. While there may be a few distantly related commonalities between these and Occam's razor, the earlier deal with dividing categories of knowledge while Occam's razor deals with the complexity of arguments for a given explanation.

Using the razor as a handwave tool

Woo-meisters and creationists sometimes use Occam's razor incorrectly as a handwave to avoid facing the fact that the point they are arguing requires a completely unknown mechanism (paranormal powers, Goddidit, aliensdidit, etc.) to work properly. This claim states that Occam's razor prefers to assume that a god (or similar device) does exist and it's simpler to believe Goddidit than that natural selection and evolution could create the complexity of life. This ignores the incredible complexity such an entity would require, and that since very few religions totally deny the existence of observable natural mechanisms, they are arguing that the entity exists in addition to all of the terms their opponent is assuming. It's also quite easy for skeptics to fall for this one, citing Occam's razor as evidence itself, rather than finding evidence to refute a concept.

Related ideas

It's as if Inigo Montoya woke up in Coruscant.

Occam's duct tape

The opposite mental process to Occam's razor — avoiding simplicity and making as many (potentially) unnecessary assumptions as possible — is sometimes referred to as Occam's duct tape.

Crabtree's bludgeon

Crabtree's bludgeon is an observation which serves as a foil to Occam's razor, characterizing a very different cognitive process exhibited in certain kinds of people, which states:

“”No set of mutually inconsistent observations can exist for which some human intellect cannot conceive a coherent explanation, however complicated.[4]

Newton's flaming laser sword

Newton's flaming laser sword, also known as Alder's razor, is another sort of razor devised by the Australian mathematician and philosopher Mike Alder. It represents a sort of logical positivism that is a common thread among the sciences. It states: "What cannot be settled by experiment is not worth debating."

Alder characterizes the flaming laser sword as "much sharper and more dangerous than Occam's razor."[5]

The opposite mental process to the flaming laser sword is Newton's arc welder or Alder's duct tape - avoiding (open) debate to obviate experiments or debating documented experiments to keep a question unsettled.

Trump's razor

When there are several explanations for any one of Donald Trump's policies, assume the most stupid one applies.[6]

See also

• Begging the question
• Hanlon's razor
• Parsimony
• Thomas Aquinas, who had a response
• Pierre D'Ailly
• Conspiracy theories
• Extraordinary claims require extraordinary evidence

References

1. https://twitter.com/elonmusk/status/944787213430034432
2. Solomonoff induction, wiki.lesswrong.com.
3. https://www.britannica.com/biography/William-of-Ockham
4. At the Christmas party, British Medical Journal
5. Newton’s Flaming Laser Sword, Philosophy Now
6. The Continuing Triumph of Trump’s Razor by Josh Marshall (May 11, 2017 4:32 pm) Talking Points Memo.