17
3
The Challenge
You must calculate pi in the shortest length you can. Any language is welcome to join and you can use any formula to calculate pi. It must be able to calculate pi to at least 5 decimal places. Shortest, would be measured in characters. Competition lasts for 48 hours. Begin.
Note: This similar question states that PI must be calculated using the series 4 * (1 – 1/3 + 1/5 – 1/7 + …). This question does not have this restriction, and in fact a lot of answers here (including the most likely to win) would be invalid in that other question. So, this is not a duplicate.
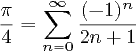

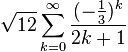
1Does it actually have to calculate pi? The shortest answers will cheat by just storing 3.14159 in a variable, start calculating from there, see that it is already known to 5 decimal places, and just print it. – hvd – 2014-02-24T20:44:10.103
It has to actually calculate pi and not just display a predefined variable or function containing pi. – poseidon – 2014-02-24T20:45:07.757
2Presumably anyone that just does 4*atan(1) should be disqualified, but it does actually calculate pi, and uses a function that does not itself contain pi. – hvd – 2014-02-24T20:58:34.353
5@hvd Why do you think it should be disqualified? It fits the specs ... – Dr. belisarius – 2014-02-24T21:53:00.887
@belisarius Well, if my objection is with the specs, pointing out that the specs allow it doesn't help. :) The OP's comment isn't part of the specs either, so if I find a language that allows
π+0, that's a three-character answer, and the OP has already clarified that such answers are intended to be invalid. I don't really see4*atan(1)as less of a cheat than that one. – hvd – 2014-02-24T22:12:56.707@hvd Ok. Perhaps a better definition of "calculation" is in order hre – Dr. belisarius – 2014-02-24T22:16:16.283
5@hvd acos(-1). I win! – Level River St – 2014-02-24T23:47:15.677
@hvd - i've seen answers , like mine that can beat a variable with 3.14159 in it
– TheDoctor – 2014-02-25T02:05:37.143I was originally more thinking of calculating an actual equation, like the "Libenz"(I think that is how it is spelt) equation or something similar. Not just a simple calculation, however, well done for thinking outside of the box, to those who did just do simple calculation. I am unsure as to whether to pick the actual equation ones or the just simple calculation answers as the best. Anyway, there's still over 29 hours to go, so carry on! – poseidon – 2014-02-25T16:33:56.470
1The question that is linked (making this a supposed duplicate) state that PI must be calculated using the series
4 * (1 – 1/3 + 1/5 – 1/7 + …). This question does not have this restriction, and in fact a lot of answers here (including the most likely to win) would be invalid in that other question. So, this is not a duplicate. – Victor Stafusa – 2014-02-25T16:36:24.4701Very true Victor. – poseidon – 2014-02-25T16:37:01.873
@Poseidon Re: Libenz: You would have done well to put "no trig functions" in the question. However none of the three most popular answers at the moment uses a trig function, and first and third most popular (ace, jpjacobs) are among the shortest anyway. Neither of the 6 char answers uses a trig function (but one of them uses a conversion of 180 degrees.) – Level River St – 2014-02-25T18:47:36.817
4This looks weird, inconsistent. Calculating π has to be dividing a circle by its diameter, or some other operation giving π. If we accept doing 355/113 — which has nothing to do with π except luck —, like @ace, then logically we should accept doing 3.14159. – Nicolas Barbulesco – 2014-02-25T20:07:05.400
But @poseidon wants the solution to calculate. Let’s calculate… :-) – Nicolas Barbulesco – 2014-02-25T20:09:11.723
7I don't get why people like this question. This is one of the most ill-defined and uninteresting questions I've seen on here. The only difference between this and hello world, is that this has something to do with Pi. – Cruncher – 2014-02-25T21:54:23.277
@Cruncher It is a simple and easy question where everyone, even with poor programming skills, can answer something acceptable in less than 10 minutes, not a hard question where I need 1 hour just to understand what I am supposed to do. – Victor Stafusa – 2014-02-26T00:30:44.933
1@poseidon Can you please add a rule that explicitly prohibits the use of built-in trigonometric functions? Seriously guys, you can't honestly believe that typing your favorite language's variant of
acos(-1)is somehow in the spirit of this question (and for that matter, neither is your favorite approximate reduction of314159 / 100000). – Jason C – 2014-02-26T03:46:50.3833
I just finished looking through all the answers here so far. I mean really guys, of course you can find a language that let's you call somebody else's implementation of the calculation in as few characters as possible, but how is that even remotely interesting? Saying "hey guys don't forget, language X has an atan() too" is roughly equivalent to posting a link to your favorite language's documentation. Who wants to see that? If you can't be bothered to find a solution like Yimin Rong's, don't bother.
– Jason C – 2014-02-26T04:12:38.6008To make this question interesting it needs a scoring function that rewards digits of pi per byte of code. – Ben Jackson – 2014-02-26T05:16:38.230
x86 Machine Language - 2 bytes The FLDPI assembly instruction translates to 0xD9EB in machine language - thus it could count as a 2-byte solution. – Steve S. – 2014-02-26T00:51:32.157
1It should be obvious that almost none of these people are actually calculating pi (piet solution aside). They either use Pi as part of their solution (trig identities), or are calculating an approximation of pi. It's impossible to use their solutions to ever actually get closer than they provided to PI without already having it. Anyone arguing against is just trying to make this question boring and prohibitively easy because they don't know enough math to be creative. – VoronoiPotato – 2014-02-26T13:45:37.033
1@JasonC Is this a joke? This isn't a popularity contest. This is tagged code golf. Why would somebody not use the shortest code that solves the problem. That IS what code golf is. When something leads to uninteresting answers, its because of an uninteresting question (see my earlier comment). – Cruncher – 2014-02-26T13:45:57.113
3@JasonC The question explicitly says calculate it to 5 decimal places. That is literally equivalent to saying "Make your program output 3.14159". It could potentially be much more interesting if the program had to accept the accuracy as a parameter. – Cruncher – 2014-02-26T13:47:02.900
@Cruncher because it doesn't actually solve the problem. The question asks you to "Calculate Pi" to 5 digits. Identities aren't calculation, you might as well go pi = 3.14159. Typing it in isn't the same as calculating it, you're merely asserting a reality. If I asked how you got it you would just shrug. – VoronoiPotato – 2014-02-26T13:47:30.417
1@VoronoiPotato "Calculate Pi" isn't particularly well defined. Especially saying "Calculate Pi" to 5 decimal places, means calculate an approximation. Anything the computer does is some form of computation. Again, it would be much more interesting if the program had to take accuracy as a parameter. Otherwise hardcoding is always the best solution. Programs should be formed in an input => output fashion. Restrictions on how the output is to be found, leads to questions like this. – Cruncher – 2014-02-26T13:52:07.890
@Cruncher you do realize that saying that because a computer did it it's some kind of computation is ridiculously reductive. Could someone with appropriate rep edit the question so that it excludes these identity driven answers. – VoronoiPotato – 2014-02-26T13:56:39.933
@VoronoiPotato And invalidate the highest voted answer that was valid when it was posted? In any case, you're welcome to edit it and try to get it approved. In doing so you will arrive at the intrinsic problems here. You can't exclude a special case for everything. – Cruncher – 2014-02-26T13:58:08.980
@Cruncher I'd argue that it wasn't valid, because it's not a calculation it's a thinly veiled assertion. I think there's a difference from trying to exclude a special case for everything and responding to literally the first comment on the question. – VoronoiPotato – 2014-02-26T14:03:55.850
@JasonC No I don't think its what the OP had in mind. It's just a bad question. – Cruncher – 2014-02-26T16:29:35.680
1@poseidon Does it need to display the answer, or does it just need to calculate the value and store it somewhere? – Jason C – 2014-02-26T16:46:29.147
1Come on guys, really... no more forms of
3.14159*a/a- The only difference between355/113and3.14159/1is a=113 instead of 1; what's the cut off fora? And how many levels of algebraic identities must be present for it to count?piis not OK butln(e^pi)is... ? (Sorry, I deleted my first previous comment by accident, then had to delete the second due to lack of context). – Jason C – 2014-02-26T17:07:44.8903Backrolled to revision 3. A competition which last 48 hours shouldn't have it's rules changed less than 8 hours before it ends. Also, @poseidon, if you tag a competition as [tag:code-golf], common courtesy would dictate that you also select the shortest answer. – primo – 2014-02-27T01:35:07.823
1@poseidon Why did you pick ace's answer? Ignoring the fact that selecting a trig function / algebraic identity answer makes this question a categorical fail, it's not even the shortest solution posted. Double fail; or maybe that's
226*fail/113. – Jason C – 2014-02-27T02:04:33.7803Yup. Level of unimpressed exceeds 9000 on this. – amcgregor – 2014-02-27T20:56:59.023
@Primo — Shortest does not mean nicest. In fact, it is often the opposite. – Nicolas Barbulesco – 2014-02-28T15:40:37.720
@NicolasBarbulesco Shortest is an objective winning criteria. Nicest is not. – primo – 2014-02-28T18:19:32.357
You should have made this a [tag:popularity-contest] at least... – Tobias Kienzler – 2014-03-01T10:13:02.913