Calculate pi to 5 decimals

Question

This comes from http://programmers.blogoverflow.com/2012/08/20-controversial-programming-opinions/

"Given that Pi can be estimated using the function 4 * (1 – 1/3 + 1/5 – 1/7 + …) with more terms giving greater accuracy, write a function that calculates Pi to an accuracy of 5 decimal places."

• Note, the estimation must be done by calculating the sequence given above.

Answer 1

JavaScript, 46 58 56 45 bytes

ES6 update: Turns out there's more features available to us now that five years have passed.

let f=(i=0,a=0)=>i>1e6?a:f(i+4,a+8/-~i/(i+3))

This version (45 bytes; yes, the let is required) works in ES6 strict mode in theory. In practice, you can run it in V8 (e.g. with node) with --use-strict --harmony-tailcalls; the Proper Tailcalls feature isn't widely implemented yet, alas. However, it's specified behaviour, so it should be fine.

If we want to stick to what's widely implemented, and not require strict-mode, we can simply use the ES6 fat-arrow syntax for functions but otherwise retain the same implementation as before (suggested by Brian H) for a cost of 48 bytes.

a=>{for(a=i=0;i<1e6;a+=8/++i/~-(i+=3));return a}

The choice of name for the single parameter doesn't really matter, but we might as well pick one of the names we use so as to minimise the global-scope pollution.

---

function(){for(a=i=0;i<1e6;a+=8/++i/~-(i+=3));return a}

This version is a function expression; add two characters (e.g. " f") if you want it named. This version clobbers the globals a and i; this could be prevented if we added "a,i" to the parameter list.

Makes use of a reformulated version of the algorithm in order to circumvent the need for subtraction.

 1/1 - 1/3  +   1/5 - 1/7   +    1/9 - 1/11  + ...
(3/3 - 1/3) + (7/35 - 5/35) + (11/99 - 9/99) + ...
    2/3     +      2/35     +       2/99     + ...
  2/(1*3)   +    2/(5*7)    +     2/(9*11)   + ...

Here's a "plain" version without this adjustment:

function(){for(a=0,i=1;i<1e6;i+=2)a+=[,4,,-4][i%4]/i;return a}

which clocks in at 64 62 characters.

Thanks to @ardnew for the suggestion to get rid of the 4* before the return.

---

History

function(){for(a=i=0;i<1e6;a+=8/++i/~-(i+=3));return a}     // got rid of `i+=4`; restructured
// Old versions below.
function(){for(a=0,i=1;i<1e6;i+=4)a+=8/i/-~-~i;return a}    // got rid of `4*`
function(){for(a=0,i=1;i<1e6;i+=4)a+=2/i/-~-~i;return 4*a}

Answer 2

Python 59 bytes

print reduce(lambda x,p:p/2*x/p+2*10**999,range(6637,1,-2))

This prints out 1000 digits; slightly more than the required 5. Instead of using the prescribed iteration, it uses this:

pi = 2 + 1/3*(2 + 2/5*(2 + 3/7*(2 + 4/9*(2 + 5/11*(2 + ...)))))

The 6637 (the innermost denominator) can be formulated as:

digits * 2*log2(10)

This implies a linear convergence. Each deeper iteration will produce one more binary bit of pi.

If, however, you insist on using the tan^-1 identity, a similar convergence can be achieved, if you don't mind going about the problem slightly differently. Taking a look at the partial sums:

4.0, 2.66667, 3.46667, 2.89524, 3.33968, 2.97605, 3.28374, ...

it is apparent that each term jumps back and forth to either side of the convergence point; the series has alternating convergence. Additionally, each term is closer to the convergence point than the previous term was; it is absolutely monotonic with respect to its convergence point. The combination of these two properties implies that the arithmetic mean of any two neighboring terms is closer to the convergence point than either of the terms themselves. To give you a better idea of what I mean, consider the following image:

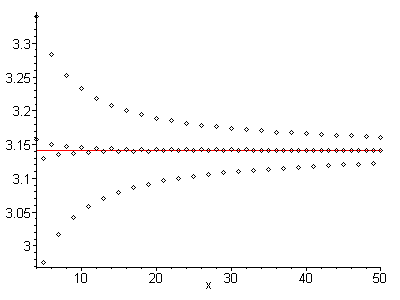
The outer series is the original, and the inner series is found by taking the average of each of the neighboring terms. A remarkable difference. But what's truly remarkable, is that this new series also has alternating convergence, and is absolutely monotonic with respect to its convergence point. That means that this process can be applied over and over again, ad nauseum.

Ok. But how?

Some formal definitions. Let P₁(n) be the n^th term of the first sequence, P₂(n) be the n^th term of the second sequence, and similarly P_k(n) the n^th term of the k^th sequence as defined above.

P₁ = [P₁(1), P₁(2), P₁(3), P₁(4), P₁(5), ...]

P₂ = [(P₁(1) +P₁(2))/2, (P₁(2) +P₁(3))/2, (P₁(3) +P₁(4))/2, (P₁(4) +P₁(5))/2, ...]

P₃ = [(P₁(1) +2P₁(2) +P₁(3))/4, (P₁(2) +2P₁(3) +P₁(4))/4, (P₁(3) +2P₁(4) +P₁(5))/4, ...]

P₄ = [(P₁(1) +3P₁(2) +3P₁(3) +P₁(4))/8, (P₁(2) +3P₁(3) +3P₁(4) +P₁(5))/8, ...]

Not surprisingly, these coefficients follow exactly the binomial coefficients, and can expressed as a single row of Pascal's Triangle. Since an arbitrary row of Pascal's Triangle is trivial to calculate, an arbitrarily 'deep' series can be found, simply by taking the first n partial sums, multiply each by the corresponding term in the k^th row of Pascal's Triangle, and dividing by 2^k-1.

In this way, full 32-bit floating point precision (~14 decimal places) can be achieved with just 36 iterations, at which point the partial sums haven't even converged on the second decimal place. This is obviously not golfed:

# used for pascal's triangle
t = 36; v = 1.0/(1<<t-1); e = 1
# used for the partial sums of pi
p = 4; d = 3; s = -4.0

x = 0
while t:
  t -= 1
  p += s/d; d += 2; s *= -1
  x += p*v
  v = v*t/e; e += 1

print "%.14f"%x

If you wanted arbitrary precision, this can be achieved with a little modification. Here once again calculating 1000 digits:

# used for pascal's triangle
f = t = 3318; v = 1; e = 1
# used for the partial sums of pi
p = 4096*10**999; d = 3; s = -p

x = 0
while t:
  t -= 1
  p += s/d; d += 2; s *= -1
  x += p*v
  v = v*t/e; e += 1

print x>>f+9

The initial value of p begins 2¹⁰ larger, to counteract the integer division effects of s/d as d becomes larger, causing the last few digits to not converge. Notice here again that 3318 is also:

digits * log2(10)

The same number of iteratations as the first algorithm (halved because t decreases by 1 instead of 2 each iteration). Once again, this indicates a linear convergence: one binary bit of pi per iteration. In both cases, 3318 iterations are required to calculate 1000 digits of pi, as slightly better quota than 1 million iterations to calculate 5.

Answer 3

Mathematica 42 39 34 33 31 26 32

Archimedes' Approach 26 chars

N@#*Sin[180 Degree/#]&

This reaches the criterion when input is 822.

Question: Does anyone know how he computed the Sin of 180 degrees? I don't.

---

Leibniz' Approach (Gregory's series) 32 chars

This is the same function the problem poser gave as an example. It reaches the criterion in approximately one half million iterations.

N@4Sum[(-1)^k/(2k+1),{k,0,10^6}]

---

Madhava-Leibniz Approach 37 chars

This variation uses a few more characters but converges to criterion in only 9 iterations!

N@Sqrt@12 Sum[(-1/3)^k/(2k+1),{k,0,9}]

Answer 4

Java (67 chars)

float r(){float p=0,s=4,i=1E6f;while(--i>0)p+=(s=-s)/i--;return p;}

Note that this avoids loss of significance by adding the numbers up in the correct order.

Answer 5

Haskell, 32

foldr(\k->(4/(2*k+1)-))0[0..8^7]

GHCi> foldr(\k->(4/(2*k+1)-))0[0..8^7]
3.141593130426724

Counting a function name it's

34

π=foldr(\k->(4/(2*k+1)-))0[0..8^7]

Answer 6

APL (14)

4×-/÷1-⍨2×⍳1e6

 

Answer 7

J, 26 chars

+/+/_2((4 _4)&%)>:+:i.100

Moved from 100 items of sequence to 1e6 items. Also now it's a code tagged and could be copypasted from browser to the console without errors.

+/+/_2((4 _4)&%)\>:+:i.1e6

Answer 8

C (GCC) (44 chars)

float p(i){return i<1E6?4./++i-p(++i):0;}

That's 41 chars, but it also has to be compiled with -O2 to get the optimiser to eliminate the tail recursion. This also relies on undefined behaviour with respect to the order in which the ++ are executed; thanks to ugoren for pointing this out. I've tested with gcc 4.4.3 under 64-bit Linux .

Note that unless the optimiser also reorders the sum, it will add from the smallest number, so it avoids loss of significance.

Call as p().

Answer 9

R - 25 chars

sum(c(4,-4)/seq(1,1e6,2))

Answer 10

Ruby - 82 chars

def f(n,k=n)k>0?(f(n,k-1)+f(n+1,k-1))/2:n<0?0:f(n-1,0)+(-1)**n/(2*n+1.0)end;4*f(9)

Try it : https://repl.it/LQ8w

The approach uses the given series indirectly using a numerical acceleration approach. The resulting output is

pi ≈ 3.14159265161

vs.

pi = 3.14159265359

It starts with

f(n,0) = 1/1 - 1/3 + 1/5 - ... + ((-1)**n)/(2*n+1)

And then, since this is alternating, we can accelerate the convergence using

f(n,1) = (f(n,0) + f(n+1,0))/2

And it repeatedly applies this:

f(n,k) = (f(n,k-1) + f(n+1,k-1))/2

And for simplicity, f(n) = f(n,n).

---

Ruby - 50 chars

If you don't mind running for a really long while, then you could simply use

def f(n)n<0?0:f(n-1)+(-1)**n/(2*n+1.0)end;4*f(1e7)

or

a=0;for k in 0..1e7 do a+=(-1)**k/(2*k+1.0)end;4*a

Answer 11

Javascript - 33 Characters

p=x=>4*(1-(x&2))/x+(x>1?p(x-2):0)

Call p passing a positive odd number x and it will calculate Pi with (x-1)/2 terms.

Answer 12

Perl - 43 39 chars

not sure the rules on anonymous subroutines, but here's another implementation using @FireFly's series construction

sub{$s+=8/((4*$_+2)**2-1)for 0..1e6;$s}

sub p{$s+=(-1)**$_*4/(2*$_+1)for 0..1e6;$s}

Answer 13

C, 69 chars

float p,b;void main(a){b++<9e6?p+=a/b++,main(-a):printf("%f\n",4*p);}

• Run with no command line parameters (so a is initialized to 1).
• Must be compiled with optimization.
• void main is strange and non-standard, but makes things work. Without it, the recursion is implemented as a real call, leading to a stack overflow. An alternative is adding return.
• Two characters 4* can be saved, if running with three command line parameters.

Answer 14

Clojure - 79 chars

(fn [](* 4(apply +(map #(*(Math/pow -1 %1)(/ 1.0(+ 1 %1 %1)))(range 377000)))))

This creates a function of no arguments which will calculate a float which approximates pi correctly to five decimal places. Note that this does not bind the function to a name such as pi, so this code must either be evaluated in place with eval as (<code>) or bound to a name in which case the solution is

(defn p[](* 4(apply +(map #(*(Math/pow -1 %1)(/ 1.0(+ 1 %1 %1)))(range 377000)))))

for 82 chars

About

(defn nth-term-of-pi [n] (* (Math/pow -1 n) (/ 1.0 (+ 1 n n))))
(defn pi [c] (* 4 (apply + (map nth-term-of-pi (range c)))))
(def  pi-accuracy-constant (loop [c 1000] (if (< (pi c) 3.14159) (recur (inc c)) c)))
; (pi pi-accuracy-constant) is then the value of pi to the accuracy of five decimal places

Answer 15

PHP - 56 55 chars

<?for($j=$i=-1;1e6>$j;){$p+=($i=-$i)/($j+=2);}echo$p*4;

I don't know that I can get it much smaller without breaking the algorithm rule.

Answer 16

SQL, 253 bytes

DECLARE @B int=3, @A varchar(max), @C varchar(max)='1'
WHILE @B<100000
BEGIN
SELECT @C=@C+(select case when (@B-1)%4=0 then'+'else'-'end)+
(SELECT cast(cast(1.0/@B as decimal(9,8)) as varchar(max)))
SELECT @B=@B+2
END
EXECUTE('SELECT 4*('+@C+')')

I would provide a SQL Fiddle, but this goes too many loops deep finding the 1/3 1/5 1/7 etc. fractions and gives errors lol. However, if you change @B<100000 to 1000 then it runs (obviously not to the same number of digits of accuracy).

Answer 17

Befunge, 129 bytes

p08p109p^v*86%+55:<$$$<
\$\>:#,_@>+\55+/:#^_"."
v>p"~"/:"~"%08p"~"/00p:2\4%-*"(}"
8^90%"~":+2:+g90*+g80*<
>*:**\/+>"~~"00g:"~"`!|

Try it online!

In case anyone is wondering, it's an elephant.

Answer 18

CJam - 21

1e6{WI#4d*I2*)/}fI]:+

Pretty straightforward calculation of the given series.
CJam is http://sf.net/p/cjam

Answer 19

Julia - 30 characters

sum(4./[1:4:1e6] - 4./[3:4:1e6])

Answer 20

Java - 92 84 chars

I cannot beat by far Peter Taylor's result, but here is mine:

double d(){float n=0,k=0,x;while(n<9E5){x=1/(1+2*n++);k+=(n%2==0)?-x:x;}return 4*k;}

Ungolfed version:

double d() {
    float n = 0, k = 0, x;
    while (n < 9E5) {
        x = 1 / (1 + 2 * n++);
        k += (n % 2 == 0) ? -x : x;
    }
    return 4 * k;
}

Edit: Saved a few characters using ternary operator.

Answer 21

Ruby - 54 chars

def a()p=0;1000000.times{|i|p+=8/(4*i*(4*i+2))};p;end;

My first try on console

def a()i=1;p=0;while i<2**100 do p+=8/(i*(i+2));i+=4;end;p;end;

63 chars.

Answer 22

Python - 56 chars

Meh, My python-fu is not strong enough. I couldn't see any more shortcuts but maybe a more experienced golfer could find something to trim here?

t=s=0
k=i=1
while t<1e6:t,s,i,k=t+1,k*4./i+s,i+2,-k

Answer 23

k (25 chars)

4*+/%(i#1 -1)'1+2!i:1000000

Slightly shorter:

+/(i#4 -4)%1+2*!i:1000000

Answer 24

Perl (76 chars)

$y=1e4;for$x(0..1e4-1){$y--while sqrt($x**2+$y**2)>1e4;$a+=$y}print 4*$a/1e8

(Result: 3.14159052)

Not the shortest possible solution, but maybe interesting. It's a geometrical one. I calculate the area under a circle.

I got another funny approach, but it's really slow. It counts the number of discrete points in a square that are below a quarter circle and calculates pi from it:

$i=shift;for$x(0..$i){for$y(0..$i){$h++if sqrt($x**2+$y**2)<$i}}print$h*4/$i**2

It expects the number of iterations as command line argument. Here you can see how run time relates to accuracy. ;)

$ time perl -e '$i=shift;for$x(0..$i){for$y(0..$i){$h++if sqrt($x**2+$y**2)<$i}}print$h*4/$i**2' 100
3.1796
real    0m0.011s
user    0m0.005s
sys 0m0.003s

$ time perl -e '$i=shift;for$x(0..$i){for$y(0..$i){$h++if sqrt($x**2+$y**2)<$i}}print$h*4/$i**2' 1000
3.14552
real    0m0.354s
user    0m0.340s
sys 0m0.004s

$ time perl -e '$i=shift;for$x(0..$i){for$y(0..$i){$h++if sqrt($x**2+$y**2)<$i}}print$h*4/$i**2' 10000
3.14199016
real    0m34.941s
user    0m33.757s
sys 0m0.097s

Answer 25

Python (49)

print 4*sum((-1)**i/(2*i+1.)for i in range(9**6))

3.14159453527