115
26
Your goal is to write a program that prints a number. The bigger the number, the more points you'll get. But be careful! Code length is both limited and heavily weighted in the scoring function. Your printed number will be divided by the cube of the number of bytes you used for your solution.
So, let's say you printed 10000000 and your code is 100 bytes long. Your final score will be 10000000 / 100^3 = 10.
There are other rules to follow, in order to make this challenge a bit harder.
- You cannot use digits in your code (0123456789);
- You can use mathematical/physical/etc. constants, but only if they are less than 10. (e.g. You can use Pi ~= 3.14 but you can't use the Avogadro constant = 6e23)
- Recursion is allowed but the generated number needs to be finite (so infinite is not accepted as a solution. Your program needs to terminate correctly, assuming unbounded time and memory, and generate the requested output);
- You cannot use the operations
*(multiply),/(divide),^(power) nor any other way to indicate them (e.g.2 div 2is not allowed); - Your program can output more than one number, if you need it to do that. Only the highest one will count for scoring;
- However, you can concatenate strings: this means that any sequence of adjacent digits will be considered as a single number;
- Your code will be run as-is. This means that the end-user cannot edit any line of code, nor he can input a number or anything else;
- Maximum code length is 100 bytes.
Leaderboard
- Steven H., Pyth ≈ fφ(1,0,0)+7(25626)/1000000[1]
- Simply Beautiful Art, Ruby ≈ fφ121(ω)(126)[1]
- Peter Taylor, GolfScript ≈ fε0+ω+1(17)/1000 [1]
- r.e.s., GolfScript ≈ fε0(fε0(fε0(fε0(fε0(fε0(fε0(fε0(fε0(126))))))))) [1]
- Simply Beautiful Art, Ruby ≈ fωω2+1(1983)
- eaglgenes101, Julia ≈ fω3(127)
- col6y, Python 3, ≈ (127→126→...→2→1) / 993 [1][3]
- Toeofdoom, Haskell, ≈ a20(1) / 993 [1]
- Fraxtil, dc, ≈ 15 ↑¹⁶⁶⁶⁶⁶⁵ 15 / 1003 [3]
- Magenta, Python, ≈ ack(126,126)/1003 ≈ 10 ↑124 129
- Kendall Frey, ECMAScript 6, ≈ 10 3 ↑4 3 / 1003 [1]
- Ilmari Karonen, GolfScript, ≈ 10 ↑3 10377 / 183 [1]
- BlackCap, Haskell, ≈ 10↑↑65503/1003
- recursive, Python, ≈ 2↑↑11 / 953 ≈ 10↑↑8.63297 [1][3]
- n.m., Haskell, ≈ 2↑↑7 / 1003 ≈ 10↑↑4.63297 [1]
- David Yaw, C, ≈ 10104×1022 / 833 ≈ 10↑↑4.11821 [2]
- primo, Perl, ≈ 10(12750684161!)5×227 / 1003 ≈ 10↑↑4.11369
- Art, C, ≈ 10102 × 106 / 983 ≈ 10↑↑3.80587
- Robert Sørlie, x86, ≈ 102219+32 / 1003 ≈ 10↑↑3.71585
- Tobia, APL, ≈ 1010353 / 1003 ≈ 10↑↑3.40616
- Darren Stone, C, ≈ 101097.61735 / 983 ≈ 10↑↑3.29875
- ecksemmess, C, ≈ 102320 / 1003 ≈ 10↑↑3.29749
- Adam Speight, vb.net, ≈ 105000×(264)4 / 1003 ≈ 10↑↑3.28039
- Joshua, bash, ≈ 101015 / 863 ≈ 10↑↑3.07282
Footnotes
- If every electron in the universe were a qubit, and every superposition thereof could be gainfully used to store information (which, as long as you don't actually need to know what's being stored is theoretically possible), this program requires more memory than could possibly exist, and therefore cannot be run - now, or at any conceiveable point in the future. If the author intended to print a value larger than ≈3↑↑3.28 all at once, this condition applies.
- This program requires more memory than currently exists, but not so much that it couldn't theoretically be stored on a meager number of qubits, and therefore a computer may one day exist which could run this program.
- All interpreters currently available issue a runtime error, or the program otherwise fails to execute as the author intended.
- Running this program will cause irreparable damage to your system.
Edit @primo: I've updated a portion of the scoreboard using a hopefully easier to compare notation, with decimals to denote the logarithmic distance to the next higher power. For example 10↑↑2.5 = 1010√10. I've also changed some scores if I believed to user's analysis to be faulty, feel free to dispute any of these.
Explanation of this notation:
If 0 ≤ b < 1, then a↑↑b = ab.
If b ≥ 1, then a↑↑b = aa↑↑(b-1).
If b < 0, then a↑↑b = loga(a↑↑(b+1)).
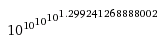
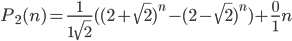









 and
and 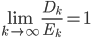




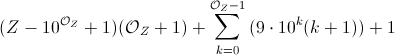
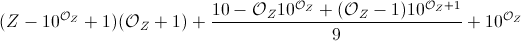
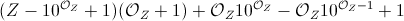
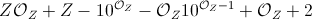
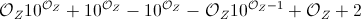
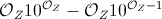

This question is the subject of a meta question – Peter Taylor – 2016-12-21T16:42:57.387
15I'm still waiting to see someone earn footnote [4]. – Brian Minton – 2017-05-18T15:41:05.270
@hichris123 I think that counts as exponentiation. – Simply Beautiful Art – 2017-05-21T20:23:47.837
1Say, if my program prints
500b, is this invalid? That is, may we ignore all non-numeric things a program prints? And if so, would something like50r7count as507? – Simply Beautiful Art – 2017-05-22T20:07:57.047I cannot find a language nor a constant that does, but what about a constant
xthat isx<-10? – Zacharý – 2017-06-14T17:51:26.99016Has someone explicitly said "base 10" yet? – keshlam – 2014-01-09T14:42:47.837
1Does the large number count if it's say
12e10(1210^10) as `1210^10`? – hichris123 – 2014-01-09T19:36:25.0674I think a better constraint instead of forbidding *, /, and ^, would've been to allow only linear operations, e.g. +, -, ++, --, +=, -=, etc. Otherwise, coders can take advantage of Knuth's up-arrow/Ackermann library functions if made available in their language of choice, which seems like cheating. – Andrew Cheong – 2014-01-10T00:19:29.853
Requesting change of accept votes someday. – Simply Beautiful Art – 2017-12-09T15:40:07.463
Can we output in base-256 (if our language is allowed to output in Unicode numbers normally) – MilkyWay90 – 2019-06-11T14:54:44.103