47
17
The function TREE(k) gives the length of the longest sequence of trees T1, T2, ... where each vertex is labelled with one of k colours, the tree Ti has at most i vertices, and no tree is a minor of any tree following it in the sequence.
TREE(1) = 1, with e.g. T1 = (1).
TREE(2) = 3: e.g. T1 = (1); T2 = (2)--(2); T3 = (2).
TREE(3) is a big big number. Even bigger than Graham's number. Your job is to output a number even bigger than it!
This is a code-golf so the goal is to write the shortest program in any language that deterministically outputs a number bigger than or equal to TREE(3) (to the stdout).
- You aren't allowed to take input.
- Your program must eventually terminate but you can assume the machine has infinite memory.
- You might assume your language's number type can hold any finite value but need to explain how this exactly works in your language (ex: does a float have infinite precision?)
- Infinities are not allowed as output.
- Underflow of a number type throws an exception. It does not wrap around.
- Because TREE(3) is such a complex number you can use the fast growing hierarchy approximation fϑ(Ωω ω)+1(3) as the number to beat.
- You need to provide an explanation of why your number is so big and an ungolfed version of your code to check if your solution is valid (since there is no computer with enough memory to store TREE(3))
Note: None of the answers currently found here work.
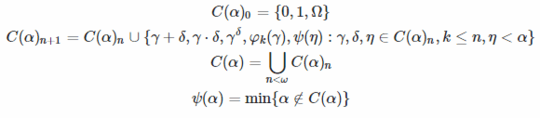
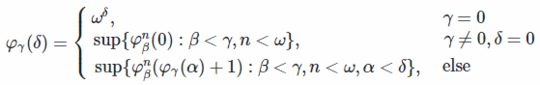
@AdmBorkBork TREE(3) is much harder to beat than Graham's number. None of the answers you list are valid here. – PyRulez – 2017-08-16T18:29:40.000
Separately from whether it's a duplicate or not, what's the winning criterion? – AdmBorkBork – 2017-08-16T18:41:28.273
@PyRulez none of those answers work, but unless I'm mistaken, they could be trivially lengthened to work. – Stephen – 2017-08-16T18:46:12.473
9@StepHen not trivally. Getting to Tree(3) requires a whole new paradigm. – PyRulez – 2017-08-16T18:58:12.750
@StepHen whoops, I always forget that. – PyRulez – 2017-08-16T19:00:25.133
@PyRulez from the (now deleted) comment about Ackermann, couldn't I just run a really big Ackermann? (and Ackermann is a builtin in several langs) – Stephen – 2017-08-16T19:01:47.880
@StepHen your input would need to be significantly bigger than Graham's number. – PyRulez – 2017-08-16T19:02:53.543
@PyRulez How will we know if we've done it? Say I define f(x) : f(2) = 2 and f(x>2) = f(x-1)^f(x-1). Is f(1000000) > TREE(3)? – benzene – 2017-08-16T19:04:26.280
@benzene you will need to use math. It doesn't look like your answer works though. I added a link describing the size of Tree(3). – PyRulez – 2017-08-16T19:05:33.927
@PyRulez It looks as though we only have weak lower bounds on Tree(3), not the actual value or upper bound expressions. What math can we use to determine if some number is larger than it? – benzene – 2017-08-16T19:12:07.170
@benzene the third note has some upper bounds. We don't have tight upper bounds, but we do have upper bounds. I listed some, in fact. – PyRulez – 2017-08-16T19:13:34.470
This paper by Friedman lends itself to very short and simple programs, but apparently the resulting function, though enormous, can't compete with TREE(3) even for very large inputs. https://pdfs.semanticscholar.org/03dc/a166fed9d17a4c3507a76a66f8e1951f7d7a.pdf
– Alon Amit – 2017-08-17T07:02:18.640"It can be an integer, float, or any other number type that language supports. This number must be bigger than what is known as TREE(3)." Normally for this kind of question we assume that big integers are unbounded (despite the practical bounds imposed by implementation), but I don't recall any previous similar question which allowed floats and I'm not sure how to interpret this permission. – Peter Taylor – 2017-08-17T07:22:42.570
@PeterTaylor you can assume that are unbounded as well. (Just no infinity.) I was just trying to be open in what I allow. – PyRulez – 2017-08-17T13:26:24.560
Possible duplicate: https://codegolf.stackexchange.com/questions/18028/largest-number-printable
– KSmarts – 2017-08-18T13:37:51.240@KSmarts that's not [tag:code-golf] – PyRulez – 2017-08-18T14:41:29.290
1
relevant: https://codegolf.meta.stackexchange.com/questions/14057/should-output-a-number-bigger-than-tree3-be-edited-an-reopened
– fejfo – 2017-10-14T06:08:18.683@fejfo I would, but I can't vote again, since I voted to reopen it once already. – PyRulez – 2017-10-14T18:24:12.733
11
TREE(3)+1there I win – HyperNeutrino – 2017-10-14T23:44:38.020@HyperNeutrino in what programming language is that valid? – PyRulez – 2017-10-14T23:56:46.147
None; it's just theoretical, and I'm being facetious :P – HyperNeutrino – 2017-10-15T00:07:40.680
1@KSmarts You do realize none of the answers there come close to TREE(3)? – Simply Beautiful Art – 2017-10-19T23:53:34.803
Couldn’t I just output strings? In output, they’re identical to integers/floats... etc. – Stan Strum – 2017-10-20T17:09:21.873
@StanStrum why not just take the length of the string, which is basically the same thing? – PyRulez – 2017-10-20T17:41:37.373
@PyRulez I don’t like using numbers > 2 ^ 31 - 1 – Stan Strum – 2017-10-20T17:42:22.027
@StanStrum but your fine with strings that big? If you want, you could output a string of 9s, and that would count as outputting a number. – PyRulez – 2017-10-20T17:53:28.073
@StanStrum this question has already been closed and reopened twice, so I don't really want to change it – PyRulez – 2017-10-20T18:03:24.670
@PyRulez That’s alright. First, I’ll need to procrastinate my work to satisfy myself. Then, I’ll head off to my bash prompt and marker board. – Stan Strum – 2017-10-20T18:04:36.097
1@Stephen In order to reach TREE(3) using Ack(k,k), k will need to be on nearly the same order of magnitude as TREE(3). In particular, k needs to be on the level of f_ϑ(Ωω ω)+1(n), which is practically speaking TREE(3). – Simply Beautiful Art – 2017-10-20T20:50:32.070
@benzene See the previous comment. – Simply Beautiful Art – 2017-10-20T20:52:07.943
Does anyone know how many digits are in TREE(3)? I've looked around and all I've found is that it's too big to easily describe. Is it more or less than
2E15? – Engineer Toast – 2017-10-23T15:22:16.983@EngineerToast about log(TREE(3)), which is much larger than tree(7) (note TREE and tree are different functions). – PyRulez – 2017-10-23T18:44:35.663
@PyRulez I couldn't find much on that but I did find something about Graham's number: "Writing out the number of digits it has would take more atoms that can be found on the planet, and that wouldn't even be remotely close!" Since
TREE(3)is insanely larger than that, I'm going to say it's longer than2E15digits. Printing9s for the next 7,000 years is not a valid solution, then. – Engineer Toast – 2017-10-23T19:14:36.573@EngineerToast See this comment. It more or less transcribes into "the amount of digits of TREE(3) are so large, that it's on the same magnitude of TREE(3)." Generally, once numbers reach the scale of
– Simply Beautiful Art – 2017-10-24T14:12:32.3101E(1E(1E(1E(1E(1E(...))))))we say "the amount of digits" looks practically the same as the number itself. (hopefully that makes sense)Is a solution like
while (i++ < INT_MAX) while (j++ < INT_MAX) while (k++ < INT_MAX) while (l++ < INT_MAX) while (m++ < INT_MAX) printf("999");allowed? – MD XF – 2017-10-26T03:25:51.8902@MDXF I'm gonna say no, because using INT_MAX is kinda a cheating (otherwise, print INT_MAX would insta win). In general, your output needs to be the same for any sufficiently large system. – PyRulez – 2017-10-26T07:30:53.957
1@MDXF also, pretty sure you won't reach TREE(3) anytime soon like that. – Simply Beautiful Art – 2017-10-26T13:57:15.990
@HyperNeutrino Okay, you win. I made an answer with TREE(3)+1. It's needs to be better golfed if its going to win though. – PyRulez – 2017-10-27T23:57:14.453
If I output a string of digits, does that count? And if I print multiple times, will we concatenate the final results? – Simply Beautiful Art – 2017-11-01T14:15:39.973
@SimplyBeautifulArt yeah, that should be fine – PyRulez – 2017-11-01T21:04:51.460
You don't fix the number of k color... If that number is fixed I in the place of color use label {1..k+1} and my TREE(k+1) is bigger than your TREE(k) – RosLuP – 2017-11-05T13:31:42.493
1@RosLuP uhm, $k=3$. If you want to do $TREE(4)$, that's fine. (You have to write a program to output it though.) – PyRulez – 2017-11-05T15:41:47.920
@ØrjanJohansen Thanks for the generosity. – Simply Beautiful Art – 2017-11-09T17:22:26.770
Public service announcement: I'm opening a Discord server dedicated to explaining ordinals and the fast growing hierarchy. The end goal will be to reach an understanding of the magnitude of TREE(3) and larger things using only recursion, and lots of it.
– Simply Beautiful Art – 2017-11-10T11:57:14.193Add the tag ([tag:tree-traversal])? – Simply Beautiful Art – 2017-11-14T16:29:16.837
@ØrjanJohansen Whoops sorry, wrong question. :P – PyRulez – 2017-11-15T04:54:10.957
See also: Ridiculously Huge numbers Part 20
– Simply Beautiful Art – 2018-03-20T23:51:18.800@SimplyBeautifulArt I'm not sure. Answers do not need to do anything with trees, and most of them do not. TREE(3) is just a number that just so happens to be defined in terms of trees. Many number of similar magnitude are not defined in terms of trees. – PyRulez – 2018-12-03T18:36:34.060