Zhihong Xia

Zhihong "Jeff" Xia (Chinese: 夏志宏; pinyin: Xia Zhihong; born 20 September 1962 in Dongtai, Jiangsu, China) is a Chinese-American mathematician.

This is a Chinese name; the family name is Xia.

Education and career

Xia's construction proving the Painlevé conjecture

Xia received in 1982 from Nanjing University a bachelor's degree in astronomy and in 1988 a PhD in mathematics from Northwestern University with thesis advisor Donald G. Saari and thesis The Existence of the Non-Collision Singularities.[1] From 1988 to 1990 Xia was an assistant professor at Harvard University and from 1990 to 1994 an associate professor at Georgia Institute of Technology (and Institute Fellow). In 1994 he became a full professor at Northwestern University and since 2000 he has been there the Arthur and Gladys Pancoe Professor of Mathematics.[2]

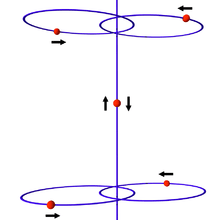
His research deals with celestial mechanics, dynamical systems, Hamiltonian dynamics, and ergodic theory. In his dissertation he solved the Painlevé conjecture, a long-standing problem posed in 1895 by Paul Painlevé. The problem concerns the existence of singularities of non-collision character in the ${\displaystyle N}$-body problem in three-dimensional space; Xia proved existence for ${\displaystyle N\geq 5}$. For the existence proof he constructed an example of five masses, of which four are separated into two pairs which revolve around each other in eccentric elliptical orbits about the z-axis of symmetry, and a fifth mass moves along the z-axis. For selected initial conditions, the fifth mass can be accelerated to an infinite velocity in a finite time interval (without any collision between the bodies involved in the example).[3] The case ${\displaystyle N=4}$ is open.[4] For ${\displaystyle N=3}$ Painlevé had proved that the singularities (points of the orbit in which accelerations become infinite in a finite time interval) must be of the collision type. However, Painlevé's proof did not extend to the case ${\displaystyle N>3}$.

In 1993 Xia was the inaugural winner of the Blumenthal Award of the American Mathematical Society. From 1989 to 1991 he was a Sloan Fellow. From 1993 to 1998, he received the National Young Investigator Award from the National Science Foundation. In 1995 he received the Monroe H. Martin Prize in Applied Mathematics from the University of Maryland.[5] In 1998 he was an Invited Speaker of the International Congress of Mathematicians in Berlin.[6]

Selected publications

• Xia, Zhihong (1992). "The Existence of Noncollision Singularities in Newtonian Systems". Annals of Mathematics. Series 2. 135 (3): 411–468. doi:10.2307/2946572. JSTOR 2946572.
• Xia, Zhihong (1992). "Existence of invariant tori in volume-preserving diffeomorphisms". Ergodic Theory and Dynamical Systems. 12 (3): 621–631. doi:10.1017/S0143385700006969.
• Xia, Zhihong (1992). "Melnikov method and transveral homoclinic points in the restricted three-body problem" (PDF). Journal of Differential Equations. 96 (1): 170–184. Bibcode:1992JDE....96..170X. doi:10.1016/0022-0396(92)90149-H.
• Saari, Donald G.; Xia, Zhihong (1993). "Off to Infinity in Finite Time" (PDF). Notices of the AMS. 42: 538–546.
• Xia, Z (1994). "Arnold diffusion and oscillatory solutions in the planar three-body problem". Journal of Differential Equations. 110 (2): 289–321. Bibcode:1994JDE...110..289X. doi:10.1006/jdeq.1994.1069.
• Saari, Donald G; Xia, Zhihong (1996). "Singularities in the Newtonian 𝑛-body problem". Hamiltonian Dynamics and Celestial Mechanics. Contemporary Mathematics. 198. American Mathematical Society. pp. 21–30. CiteSeerX 10.1.1.24.1325. doi:10.1090/conm/198/02493. ISBN 9780821805664.
• Xia, Zhihong (1996). "Homoclinic points in symplectic and volume-preserving diffeomorphisms". Communications in Mathematical Physics. 177 (2): 435–449. Bibcode:1996CMaPh.177..435X. doi:10.1007/BF02101901.
• Zhu, Deming; Xia, Zhihong (1998). "Bifurcations of heteroclinic loops". Science in China Series A: Mathematics. 41 (8): 837–848. Bibcode:1998ScChA..41..837Z. doi:10.1007/BF02871667.
• Xia, Zhihong (2004). "Convex central configurations for the n-body problem". Journal of Differential Equations. 200 (2): 185–190. Bibcode:2004JDE...200..185X. doi:10.1016/j.jde.2003.10.001.
• Xia, Zhihong (2006). "Area-preserving surface diffeomorphisms". Communications in Mathematical Physics. 263 (3): 723–735. arXiv:math/0503223. Bibcode:2006CMaPh.263..723X. CiteSeerX 10.1.1.235.4920. doi:10.1007/s00220-005-1514-3.
• Saghin, Radu; Xia, Zhihong (2009). "Geometric expansion, Lyapunov exponents and foliations" (PDF). Annales de l'Institut Henri Poincaré C. 26 (2): 689–704. Bibcode:2009AIHPC..26..689S. doi:10.1016/j.anihpc.2008.07.001.
• Xia, Zhihong; Zhang, Pengfei (2014). "Homoclinic points for convex billiards". Nonlinearity. 27 (6): 1181–1192. arXiv:1310.5279. doi:10.1088/0951-7715/27/6/1181.
• Xia, Zhihong; Zhang, Pengfei (2017). "Homoclinic intersections for geodesic flows on convex spheres". Dynamical Systems, Ergodic Theory, and Probability: in Memory of Kolya Chernov. Contemporary Mathematics. 698. American Mathematical Society. pp. 221–238.

References

1. Zhi-Hong Xia at the Mathematics Genealogy Project
2. "Zhihong Jeff Xia". Northwestern University.
3. In 1908 Edvard Hugo von Zeipel proved the surprising fact that the existence of a non-collision singularity in the ${\displaystyle N}$-body problem necessarily causes the velocity of at least one particle to become unbounded.
4. Joseph L. Gerver gave arguments (a heuristic model) for the existence of a non-collision singularity for the planar Newtonian 4-body problem — however, there is still no rigorous proof. See Gerver, Joseph L. (2003). "Noncollision Singularities: Do Four Bodies Suffice?". Exp. Math. 12 (2): 187–198. doi:10.1080/10586458.2003.10504491.
5. "Monroe H. Martin Prize". Center for Scientific Computation and Mathematical Modeling, University of Maryland, College Park.
6. Xia, Zhihong (1998). "Arnold diffusion: a variational construction". Doc. Math. (Bielefeld) Extra Vol. ICM Berlin, 1998, vol. II. pp. 867–877.