Wu experiment

The Wu experiment was a nuclear physics experiment conducted in 1956 by the Chinese American physicist Chien-Shiung Wu in collaboration with the Low Temperature Group of the US National Bureau of Standards.[1] The experiment's purpose was to establish whether or not conservation of parity (P-conservation), which was previously established in the electromagnetic and strong interactions, also applied to weak interactions. If P-conservation were true, a mirrored version of the world (where left is right and right is left) would behave as the mirror image of the current world. If P-conservation were violated, then it would be possible to distinguish between a mirrored version of the world and the mirror image of the current world.

Chien-Shiung Wu, after whom the Wu experiment is named, designed the experiment and led the team that carried out the test of the conservation of parity in 1956.

The experiment established that conservation of parity was violated (P-violation) by the weak interaction, providing a way to operationally define left and right without reference to the human body. This result was not expected by the physics community, which had previously regarded parity as a conserved quantity. Tsung-Dao Lee and Chen-Ning Yang, the theoretical physicists who originated the idea of parity nonconservation and proposed the experiment, received the 1957 Nobel Prize in physics for this result. Chien-Shiung Wu's role in the discovery was mentioned in the Nobel prize acceptance speech,[2] but was not honored until 1978, when she was awarded the first Wolf Prize.

History

Top: P-symmetry: A clock built like its mirrored image will behave like the mirrored image of the original clock.
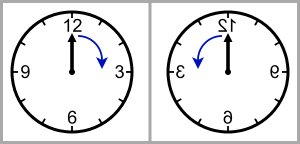
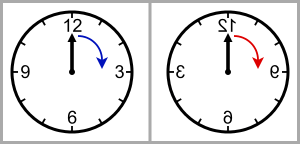
Bottom: P-asymmetry: A clock built like its mirrored image will not behave like the mirrored image of the original clock.

In 1927, Eugene Wigner formalized the principle of the conservation of parity (P-conservation),[3] the idea that the current world and one built like its mirror image would behave in the same way, with the only difference that left and right would be reversed (for example, a clock which spins clockwise would spin counterclockwise if you built a mirrored version of it).

This principle was widely accepted by physicists, and P-conservation was experimentally verified in the electromagnetic and strong interactions. However, during the mid-1950s, certain decays involving kaons could not be explained by existing theories in which P-conservation was assumed to be true. There seemed to be two types of kaons, one which decayed into two pions, and the other which decayed into three pions. This was known as the τ–θ puzzle.[4]

Theoretical physicists Tsung-Dao Lee and Chen-Ning Yang did a literature review on the question of parity conservation in all fundamental interactions. They concluded that in the case of the weak interaction, experimental data neither confirmed nor refuted P-conservation.[5] Shortly after, they approached Chien-Shiung Wu, who was an expert on beta decay spectroscopy, with various ideas for experiments. They settled on the idea of testing the directional properties of beta decay in cobalt-60. Wu realized the potential for a breakthrough experiment and began work in earnest at the end of May 1956, cancelling a planned trip to Geneva and the Far East with her husband, wanting to beat the rest of the physics community to the punch.[6][7] She therefore contacted Henry Boorse and Mark W. Zemansky, who had extensive experience in low-temperature physics. At the behest of Boorse and Zemansky, Wu contacted Ernest Ambler, of the National Bureau of Standards, who arranged for the experiment to be carried out in 1956 at the NBS' low-temperature laboratories.[4] After several months of work overcoming technical difficulties, Wu's team observed an asymmetry indicating parity violation in December 1956.[8]

Lee and Yang, who prompted the Wu experiment, were awarded the Nobel prize in physics in 1957, shortly after the experiment was performed. Wu's role in the discovery was mentioned in the prize acceptance speech,[2] but was not honored until 1978, when she was awarded the inaugural Wolf Prize.[9]

Theory

If a particular interaction respects parity symmetry, it means that if left and right were interchanged, the interaction would behave exactly as it did before the interchange. Another way this is expressed is to imagine that two worlds are constructed that differ only by parity — the "real" world and the "mirror" world, where left and right are swapped. If an interaction is parity symmetric, it produces the same outcomes in both "worlds".[1]

The aim of Wu's experiment was to determine if this was the case for the weak interaction by looking at whether the decay products of cobalt-60 were being emitted preferentially in one direction or not. This would signify the violation of parity symmetry because if the weak interaction were parity conserving, the decay emissions should be emitted with equal probability in all directions. As stated by Wu et al.:[1]

If an asymmetry in the distribution between θ and 180° − θ (where θ is the angle between the orientation of the parent nuclei and the momentum of the electrons) is observed, it provides unequivocal proof that parity is not conserved in beta decay.

The reason for this is that the cobalt-60 nucleus carries spin, and spin does not change direction under parity (because angular momentum is an axial vector). Conversely, the direction that the decay products are emitted is changed under parity because momentum is a polar vector. In other words, in the "real" world, if the cobalt-60 nuclear spin and the decay product emissions were both in roughly the same direction, then in the "mirror" world, they would be in roughly opposite directions, because the emission direction would have been flipped, but the spin direction would not.[10]

This would be a clear difference in the behaviour of the weak interaction between both "worlds", and hence the weak interaction could not be said to be parity symmetric. The only way that the weak interaction could be parity symmetric is if there were no preference in the direction of emission, because then a flip in the direction of emissions in the "mirror" world would look no different than the "real" world because there were equal numbers of emissions in both directions anyway.

Experiment

The Wu experiment performed at the Bureau of Standards low temperature laboratory, Washington DC, in 1956. The vertical vacuum chamber, containing the cobalt-60, detectors, and field coil, is being placed into a Dewar before being inserted into the large electromagnet in the background, which will cool the radioisotope near absolute zero by adiabatic demagnetization.

The experiment monitored the decay of cobalt-60 (⁶⁰Co) atoms that were aligned by a uniform magnetic field (the polarizing field) and cooled to near absolute zero so that thermal motions did not ruin the alignment.[11] Cobalt-60 is an unstable isotope of cobalt that decays by beta decay to the stable isotope nickel-60 (⁶⁰Ni). During this decay, one of the neutrons in the cobalt-60 nucleus decays to a proton by emitting an electron (e⁻) and an electron antineutrino (ν_e). The resulting nickel nucleus, however, is in an excited state and promptly decays to its ground state by emitting two gamma rays (γ). Hence the overall nuclear equation of the reaction is:

${\displaystyle {}_{27}^{60}{\text{Co}}\rightarrow {}_{28}^{60}{\text{Ni}}+e^{-}+{\bar {\nu }}_{e}+2{\gamma }}$

Gamma rays are photons, and their release from the nickel-60 nucleus is an electromagnetic (EM) process. This is important because EM was known to respect parity conservation, and therefore they would be emitted roughly equally in all directions (they would be distributed roughly "isotropically"). Hence, the distribution of the emitted electrons could be compared to the distribution of the emitted gamma rays in order to compare whether they too were being emitted isotropically. In other words, the distribution of the gamma rays acted as a control for the distribution of the emitted electrons. Another benefit of the emitted gamma rays was that it was known that the degree to which they were not distributed perfectly equally in all directions (the "anisotropy" of their distribution) could be used to determine how well the cobalt-60 nuclei had been aligned (how well their spins were aligned).[12] If the cobalt-60 nuclei were not aligned at all, then no matter how the electron emission was truly distributed it would not be detected by the experiment. This is because an unaligned sample of nuclei could be expected to be orientated randomly, and thus the electron emissions would be random and the experiment would detect equal numbers of electron emissions in all directions, even if they were being emitted from each individual nucleus in only one direction.

The experiment then essentially counted the rate of emission for gamma rays and electrons in two distinct directions and compared their values. This rate was measured over time and with the polarizing field orientated in opposite directions. If the counting rates for the electrons did not differ significantly from those of the gamma rays, then there would have been evidence to suggest that parity was indeed conserved by the weak interaction. If, however, the counting rates were significantly different, then there would be strong evidence that the weak interaction does indeed violate parity conservation.

Materials and methods

Schematic illustration of the Wu experiment

The experimental challenge in this experiment was to obtain the highest possible polarization of the ⁶⁰Co nuclei. Due to the very small magnetic moments of the nuclei as compared to electrons, high magnetic fields were required at extremely low temperatures, far lower than could be achieved by liquid helium cooling alone. The low temperatures were achieved using the method of adiabatic demagnetization. Radioactive cobalt was deposited as a thin surface layer on a crystal of cerium-magnesium nitrate, a paramagnetic salt with a highly anisotropic Landé g-factor.

The salt was magnetized along the axis of high g-factor, and the temperature was lowered to 1.2 K by pumping the helium to low pressure. Shutting off the horizontal magnetic field resulted in the temperature decreasing to about 0.003 K. The horizontal magnet was opened up, allowing room for a vertical solenoid to be introduced and switched on to align the cobalt nuclei either upwards or downwards. Only a negligible increase in temperature was caused by the solenoid magnetic field, since the magnetic field orientation of the solenoid was in the direction of low g-factor. This method of achieving high polarization of ⁶⁰Co nuclei had been originated by Gorter[13] and Rose.[14]

The production of gamma rays was monitored using equatorial and polar counters as a measure of the polarization. Gamma ray polarization was continuously monitored over the next quarter-hour as the crystal warmed up and anisotropy was lost. Likewise, beta-ray emissions were continuously monitored during this warming period.[1]

Results

In the experiment carried out by Wu, the gamma ray anisotropy was approximately 0.6.[1] That is, approximately 60% of the gamma rays were emitted in one direction, whereas 40% were emitted in the other. If parity were conserved in beta decay, the emitted electrons would have had no preferred direction of decay relative to the nuclear spin, and the asymmetry in emission direction would have been close to the value for the gamma rays. However, Wu observed that the electrons were emitted in a direction preferentially opposite to that of the gamma rays with an asymmetry significantly greater than the gamma ray anisotropy value. That is, most of the electrons favored a very specific direction of decay, specifically opposite to that of the nuclear spin.[1] The observed electron asymmetry also did not change sign when the polarizing field was reversed, meaning that the asymmetry was not being caused by remanence in the samples. It was later established that parity violation was in fact maximal.[4][15]

The results greatly surprised the physics community.[4] Several researchers then scrambled to reproduce the results of Wu's group,[16][17] while others reacted with disbelief at the results. Wolfgang Pauli upon being informed by Georges M. Temmer, who also worked at the NBS, that parity conservation could no longer be assumed to be true in all cases, exclaimed "That's total nonsense!" Temmer assured him that the experiment's result confirmed this was the case, to which Pauli curtly replied "Then it must be repeated!"[4] By the end of 1957, further research confirmed the original results of Wu's group, and P-violation was firmly established.[4]

Mechanism and consequences

The Feynman diagram for
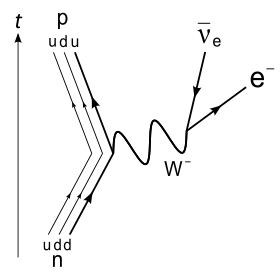
β⁻
 decay of a neutron into a proton, electron, and electron antineutrino via an intermediate
W⁻
boson.

The results of the Wu experiment provide a way to operationally define the notion of left and right. This is inherent in the nature of the weak interaction. Previously, if the scientists on Earth were to communicate with a newly discovered planet's scientist, and they had never met in person, it would not have been possible for each group to determine unambiguously the other group's left and right. With the Wu experiment, it is possible to communicate to the other group what the words left and right mean exactly and unambiguously. The Wu experiment has finally solved the Ozma problem which is to give an unambiguous definition of left and right scientifically.[18]

At the fundamental level (as depicted in the Feynman diagram on the right), Beta decay is caused by the conversion of the negatively charged (−1/3 e) down quark to the positively charged (+2/3 e) up quark by emission of a
W⁻
boson; the
W⁻
boson subsequently decays into an electron and an electron antineutrino:

d
→
u
+
e⁻
+
ν
_e.

The quark has a left part and a right part. As it walks across the spacetime, it oscillates back and forth from right part to left part and from left part to right part. From analyzing the Wu experiment's demonstration of parity violation, it can be deduced that only the left part of down quarks decay and the weak interaction involves only the left part of quarks and leptons (or the right part of antiquarks and antileptons). The right part of the particle simply does not feel the weak interaction. If the down quark did not have mass it would not oscillate, and its right part would be quite stable by itself. Yet, because the down quark is massive, it oscillates and decays.[19]

Overall, as ${\displaystyle J_{\text{Co}}=5}$, the strong magnetic field vertically polarizes the ⁶⁰
₂₇Co
nuclei such that ${\displaystyle J_{z,{\text{Co}}}=J_{\text{Co}}=+5}$. Since ${\displaystyle J_{\text{Ni}}=4}$ and the decay conserves angular momentum, ${\displaystyle J_{z,{\text{Co}}}=J_{z,{\text{Ni}}}+J_{z,e^{-}}+J_{z,\nu }=+5}$ implies that ${\displaystyle J_{z,e^{-}}=J_{z,\nu }=+1/2}$. Thus, the concentration of beta rays in the negative-z direction indicated a preference for left-handed quarks and electrons.

From experiments such as the Wu experiment and the Goldhaber experiment, it was determined that massless neutrinos must be left-handed, while massless antineutrinos must be right-handed. Since it is currently known that neutrinos have a small mass, it has been proposed that right-handed neutrinos and left-handed antineutrinos could exist. These neutrinos would not couple with the weak Lagrangian and would interact only gravitationally, possibly forming a portion of the dark matter in the universe.[20]

See also

• Neutrino
• Fermi's interaction
• Electroweak interaction
• The Ambidextrous Universe by Martin Gardner; book containing a lengthy popular discussion of parity and the Wu experiment

References

1. Wu, C. S.; Ambler, E.; Hayward, R. W.; Hoppes, D. D.; Hudson, R. P. (1957). "Experimental Test of Parity Conservation in Beta Decay". Physical Review. 105 (4): 1413–1415. Bibcode:1957PhRv..105.1413W. doi:10.1103/PhysRev.105.1413.
2. Klein, O. B. (1957). "The Nobel Prize in physics in 1957: Award ceremony speech". The Nobel Foundation. Retrieved 2 October 2018.
3. Wigner, E. P. (1927). "Über die Erhaltungssätze in der Quantenmechanik". Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch Physikalische Klasse. 1927: 375–381.

   Reproduced in Wightman, A. S., ed. (1993). The Collected Works of Eugene Paul Wigner. Vol. A. Springer. pp. 84–90. doi:10.1007/978-3-662-02781-3_7. ISBN 978-3-642-08154-5.

4. Hudson, R. P. (2001). "Reversal of the Parity Conservation Law in Nuclear Physics" (PDF). In Lide, D. R. (ed.). A Century of Excellence in Measurements, Standards, and Technology. NIST Special Publication 958. National Institute of Standards and Technology. ISBN 978-0849312472.
5. Lee, T. D.; Yang, C. N. (1956). "Question of Parity Conservation in Weak Interactions". Physical Review. 104 (1): 254–258. Bibcode:1956PhRv..104..254L. doi:10.1103/PhysRev.104.254.
6. Wu, C. S. (1973). Maglich, B. (ed.). Adventures in Experimental Physics. Gamma Volume. Princeton: World Science Communications. p. 101-123. ASIN B000ITLM9Q.
7. Lee, T. D. (2006). "New Insights to Old Problems". arXiv:hep-ph/0605017.
8. Wu, C. S. (2008). "The Discovery of the Parity Violation in Weak Interactions and Its Recent Developments" (PDF). Nishina Memorial Lectures. Lecture Notes in Physics. 746. Springer. pp. 43–70. doi:10.1007/978-4-431-77056-5_4. ISBN 978-4-431-77055-8.
9. "Chien-Shiung Wu Winner of Wolf Prize in Physics - 1978". Wolf Foundation. Retrieved 9 December 2019.
10. Boyd, S. (20 April 2016). "The Weak Interaction" (PDF). Warwick University. Retrieved 8 December 2019.
11. Wroblewski, A. K. (2008). "The downfall of parity: The revolution that happened fifty years ago" (PDF). Acta Physica Polonica B. 39 (2): 251–264. Bibcode:2008AcPPB..39..251W.
12. Ambler, E.; Grace, M. A.; Halban, H.; Kurti, N.; Durand, H.; Johnson, C. E.; Lemmer, H. R. (1953). "Nuclear polarization of cobalt 60". Taylor & Francis. 44 (349): 216–218. doi:10.1080/14786440208520296.
13. Gorter, C. J. (1948). "A New Suggestion for Aligning Certain Atomic Nuclei". Physica. 14 (8): 504. Bibcode:1948Phy....14..504G. doi:10.1016/0031-8914(48)90004-4.
14. Rose, M. E. (1949). "On the Production of Nuclear Polarization". Physical Review. 75 (1): 213. Bibcode:1949PhRv...75Q.213R. doi:10.1103/PhysRev.75.213.
15. Ziino, G. (2006). "New Electroweak Formulation Fundamentally Accounting for the Effect Known as "Maximal Parity-Violation"". International Journal of Theoretical Physics. 45 (11): 1993–2050. Bibcode:2006IJTP...45.1993Z. doi:10.1007/s10773-006-9168-2.
16. Garwin, R. L.; Lederman, L. M.; Weinrich, M. (1957). "Observations of the failure of conservation of parity and charge conjugation in meson decays: the magnetic moment of the free muon" (PDF). Physical Review. 105 (4): 1415–1417. Bibcode:1957PhRv..105.1415G. doi:10.1103/PhysRev.105.1415.
17. Ambler, E.; Hayward, R. W.; Hoppes, D. D.; Hudson, R. P.; Wu, C. S. (1957). "Further Experiments on Decay of Polarized Nuclei" (PDF). Physical Review. 106 (6): 1361–1363. Bibcode:1957PhRv..106.1361A. doi:10.1103/PhysRev.106.1361.
18. Gardner, M. (2005). The New Ambidextrous Universe: Symmetry and Asymmetry from Mirror Reflections to Superstrings (3rd Revised ed.). Courier Corporation. pp. 215–218. ISBN 978-0-486-44244-0.
19. Lederman, L. M.; Hill, C. T. (2013). Beyond the God Particle. Prometheus Books. pp. 125–126. ISBN 978-1-61614-802-7.
20. Drewes, M. (2013). "The Phenomenology of Right Handed Neutrinos". International Journal of Modern Physics E. 22 (8): 1330019–593. arXiv:1303.6912. Bibcode:2013IJMPE..2230019D. doi:10.1142/S0218301313300191.

Further reading

• Martin, W. C.; Coursey, J.; Dragoset, R. A. (July 1997). "The Fall of Parity". NIST Physical Measurement Laboratory.
• Wroblewski, A. K. (2008). "The downfall of parity: The revolution that happened fifty years ago" (PDF). Acta Physica Polonica B. 39 (2): 251–264. Bibcode:2008AcPPB..39..251W.