Wells turbine

The Wells turbine is a low-pressure air turbine that rotates continuously in one direction independent of the direction of the air flow. Its blades feature a symmetrical airfoil with its plane of symmetry in the plane of rotation and perpendicular to the air stream.

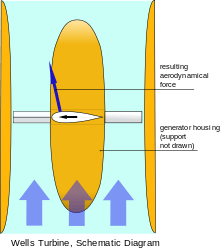
It was developed for use in Oscillating Water Column wave power plants, in which a rising and falling water surface moving in an air compression chamber produces an oscillating air current. The use of this bidirectional turbine avoids the need to rectify the air stream by delicate and expensive check valve systems.

Its efficiency is lower than that of a turbine with constant air stream direction and asymmetric airfoil. One reason for the lower efficiency is that symmetric airfoils have a higher drag coefficient than asymmetric ones, even under optimal conditions. Also, in the Wells turbine, the symmetric airfoil runs partly under high angle of attack (i.e., low blade speed / air speed ratio), which occurs during the air velocity maxima of the oscillating flow. A high angle of attack causes a condition known as "stall" in which the airfoil loses lift. The efficiency of the Wells turbine in oscillating flow reaches values between 0.4 and 0.7.

The Wells turbine was developed by Prof. Alan Arthur Wells of Queen's University Belfast in the late 1970s.

Annotation

Another solution of the problem of stream direction independent turbine is the Darrieus wind turbine (Darrieus rotor).

gollark: Want to make a backdoor in your OS but don't have a server? SPUDNET is now open to the public! SPUDNET is the more than 40% reliable backdoor relay system powering potatOS's backdoors! PM me for access.
gollark: Wasn't me.
gollark: <@!202992030685724675> Your base appears to contain more holes than is optimal.
gollark: Makes sense.
gollark: Just kind of bodgily parse it looking for variable declarations (locals, that is) and gsub them.

See also
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.