Wake


In fluid dynamics, a wake may either be:
- the region of recirculating flow immediately behind a moving or stationary blunt body, caused by viscosity, which may be accompanied by flow separation and turbulence, or
- the wave pattern on the water surface downstream of an object in a flow, or produced by a moving object (e.g. a ship), caused by density differences of the fluids above and below the free surface and gravity (or surface tension).
Wake effects caused by viscosity
The wake is the region of disturbed flow (often turbulent) downstream of a solid body moving through a fluid, caused by the flow of the fluid around the body.
For a blunt body in subsonic external flow, for example the Apollo or Orion capsules during descent and landing, the wake is massively separated and behind the body is a reverse flow region where the flow is moving toward the body. This phenomenon is often observed in wind tunnel testing of aircraft, and is especially important when parachute systems are involved, because unless the parachute lines extend the canopy beyond the reverse flow region, the chute can fail to inflate and thus collapse. Parachutes deployed into wakes suffer dynamic pressure deficits which reduce their expected drag forces. High-fidelity computational fluid dynamics simulations are often undertaken to model wake flows, although such modeling has uncertainties associated with turbulence modeling (for example RANS versus LES implementations), in addition to unsteady flow effects. Example applications include rocket stage separation and aircraft store separation.
Waves by density differences, like a water surface
In incompressible fluids (liquids) such as water, a bow wake is created when a watercraft moves through the medium; as the medium cannot be compressed, it must be displaced instead, resulting in a wave. As with all wave forms, it spreads outward from the source until its energy is overcome or lost, usually by friction or dispersion.
The non-dimensional parameter of interest is the Froude number.
Kelvin wake pattern
Waterfowl and boats moving across the surface of water produce a wake pattern, first explained mathematically by Lord Kelvin and known today as the Kelvin wake pattern.[1]
This pattern consists of two wake lines that form the arms of a chevron, V, with the source of the wake at the vertex of the V. For sufficiently slow motion, each wake line is offset from the path of the wake source by around arcsin(1/3) = 19.47° and is made up of feathery wavelets angled at roughly 53° to the path.
The inside of the V (of total opening 39° as indicated above) is filled with transverse curved waves, each of which is an arc of a circle centered at a point lying on the path at a distance twice that of the arc to the wake source. This pattern is independent of the speed and size of the wake source over a significant range of values.[2]
However, the pattern changes at high speeds (only), viz., above a hull Froude number of approximately 0.5. Then, as the source's speed increases, the transverse waves diminish and the points of maximum amplitude on the wavelets form a second V within the wake pattern, which grows narrower with the increased speed of the source.[3]
The angles in this pattern are not intrinsic properties of merely water: Any isentropic and incompressible liquid with low viscosity will exhibit the same phenomenon. Furthermore, this phenomenon has nothing to do with turbulence. Everything discussed here is based on the linear theory of an ideal fluid, cf. Airy wave theory.
Parts of the pattern may be obscured by the effects of propeller wash, and tail eddies behind the boat's stern, and by the boat being a large object and not a point source. The water need not be stationary, but may be moving as in a large river, and the important consideration then is the velocity of the water relative to a boat or other object causing a wake.
This pattern follows from the dispersion relation of deep water waves, which is often written as,
where
- g = the strength of the gravity field
- ω is the angular frequency in radians per second
- k = angular wavenumber in radians per metre
"Deep" means that the depth is greater than half of the wavelength. This formula implies that the group velocity of a deep water wave is half of its phase velocity, which, in turn, goes as the square root of the wavelength. Two velocity parameters of importance for the wake pattern are:
- v is the relative velocity of the water and the surface object that causes the wake.
- c is the phase velocity of a wave, varying with wave frequency.
As the surface object moves, it continuously generates small disturbances which are the sum of sinusoidal waves with a wide spectrum of wavelengths. Those waves with the longest wavelengths have phase speeds above v and dissipate into the surrounding water and are not easily observed. Other waves with phase speeds at or below v, however, are amplified through constructive interference and form visible shock waves, stationary in position w.r.t. the boat.
The angle θ between the phase shock wave front and the path of the object is θ = arcsin(c/v). If c/v > 1 or < −1, no later waves can catch up with earlier waves and no shockwave forms.
In deep water, shock waves form even from slow-moving sources, because waves with short enough wavelengths move slower. These shock waves are at sharper angles than one would naively expect, because it is group velocity that dictates the area of constructive interference and, in deep water, the group velocity is half of the phase velocity.
All shock waves, that each by itself would have had an angle between 33° and 72°, are compressed into a narrow band of wake with angles between 15° and 19°, with the strongest constructive interference at the outer edge (angle arcsin(1/3) = 19.47°), placing the two arms of the V in the celebrated Kelvin wake pattern.
A concise geometric construction[4] demonstrates that, strikingly, this group shock angle w.r.t. the path of the boat, 19.47°, for any and all of the above θ, is actually independent of v, c, and g; it merely relies on the fact that the group velocity is half of the phase velocity c. On any planet, slow-swimming objects have "effective Mach number" 3!
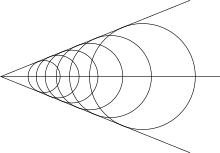
For slow swimmers, low Froude number, the Lighthill−Whitham geometric argument that the opening of the Kelvin chevron (wedge, V pattern) is universal goes as follows. Consider a boat moving from right to left with constant speed v, emitting waves of varying wavelength, and thus wavenumber k and phase velocity c(k), of interest when < v for a shock wave (cf., e.g., Sonic boom or Cherenkov radiation). Equivalently, and more intuitively, fix the position of the boat and have the water flow in the opposite direction, like a piling in a river.
Focus first on a given k, emitting (phase) wavefronts whose stationary position w.r.t. the boat assemble to the standard shock wedge tangent to all of them, cf. Fig.12.3.
As indicated above, the openings of these chevrons vary with wavenumber, the angle θ between the phase shock wavefront and the path of the boat (the water) being θ = arcsin(c/v) ≡ π/2 − ψ. Evidently, ψ increases with k. However, these phase chevrons are not visible: it is their corresponding group wave manifestations which are observed.
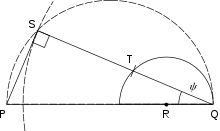
Consider one of the phase circles of Fig.12.3 for a particular k, corresponding to the time t in the past, Fig.12.2. Its radius is QS, and the phase chevron side is the tangent PS to it. Evidently, PQ= vt and SQ = ct = vt cosψ, as the right angle PSQ places S on the semicircle of diameter PQ.
Since the group velocity is half the phase velocity for any and all k, however, the visible (group) disturbance point corresponding to S will be T, the midpoint of SQ. Similarly, it lies on a semicircle now centered on R, where, manifestly, RQ=PQ/4, an effective group wavefront emitted from R, with radius vt/4 now.
Significantly, the resulting wavefront angle with the boat's path, the angle of the tangent from P to this smaller circle, obviously has a sine of TR/PR=1/3, for any and all k, c, ψ, g, etc.: Strikingly, virtually all parameters of the problem have dropped out, except for the deep-water group-to-phase-velocity relation! Note the (highly notional) effective group disturbance emitter moves slower, at 3v/4.
Thus, summing over all relevant k and ts to flesh out an effective Fig.12.3 shock pattern, the universal Kelvin wake pattern arises: the full visible chevron angle is twice that, 2arcsin(1/3) ≈ 39°.
The wavefronts of the wavelets in the wake are at 53°, which is roughly the average of 33° and 72°. The wave components with would-be shock wave angles between 73° and 90° dominate the interior of the V. They end up half-way between the point of generation and the current location of the wake source. This explains the curvature of the arcs.
Those very short waves with would-be shock wave angles below 33° lack a mechanism to reinforce their amplitudes through constructive interference and are usually seen as small ripples on top of the interior transverse waves.
Gallery
 Wake of a boat crossing an alpine lake (Koenigsee)
Wake of a boat crossing an alpine lake (Koenigsee) 39° ship wake
39° ship wake The wakes of two slow-moving boats. The nearer boat has made a striking series of ruler-straight waves
The wakes of two slow-moving boats. The nearer boat has made a striking series of ruler-straight waves A boat race with overlapping wakes, from the International Space Station, 2006
A boat race with overlapping wakes, from the International Space Station, 2006 John Harvard Biles: "The Design and Construction of Ships, Vol. II: Stability, Resistance, Propulsion and Oscillation of Ships" (1908)
John Harvard Biles: "The Design and Construction of Ships, Vol. II: Stability, Resistance, Propulsion and Oscillation of Ships" (1908) Wake from a fast, small motorboat with an outboard motor
Wake from a fast, small motorboat with an outboard motor Wake simulation
Wake simulation Kelvin wake simulation
Kelvin wake simulation
Other effects
The above describes an ideal wake, where the body's means of propulsion has no other effect on the water. In practice the wave pattern between the V-shaped wavefronts is usually mixed with the effects of propeller backwash and eddying behind the boat's (usually square-ended) stern.
The Kelvin angle is also derived for the case of deep water in which the fluid is not flowing in different speed or directions as a function of depth ("shear"). In cases where the water (or fluid) has sheer, the results may be more complicated.[5]
Recreation
"No wake zones" may prohibit wakes in marinas, near moorings and within some distance of shore[6] in order to facilitate recreation by other boats and reduce the damage wakes cause. Powered narrowboats on British canals are not permitted to create a breaking wash (a wake large enough to create a breaking wave) along the banks, as this erodes them. This rule normally restricts these vessels to 4 statute miles per hour or less.
Wakes are occasionally used recreationally. Swimmers, people riding personal watercraft, and aquatic mammals such as dolphins can ride the leading edge of a wake. In the sport of wakeboarding the wake is used as a jump. The wake is also used to propel a surfer in the sport of wakesurfing. In the sport of water polo, the ball carrier can swim while advancing the ball, propelled ahead with the wake created by alternating armstrokes in crawl stroke, a technique known as dribbling.
Image gallery
 Germany's only consistent surf spot is a giant wake from a ship
Germany's only consistent surf spot is a giant wake from a ship- Wake from a fast motor yacht on the Indian River looking at the 17th Street Bridge
_behind_a_ferry.jpg) Wake behind a ferry in the Baltic Sea
Wake behind a ferry in the Baltic Sea.jpg) Wake of a boat in the Hawaiian Islands
Wake of a boat in the Hawaiian Islands Wake of a ferryboat just off British Columbia, Canada.
Wake of a ferryboat just off British Columbia, Canada.
References
- William Thomson (1887) "On ship waves," Institution of Mechanical Engineers, Proceedings, 38 : 409–34; illustrations, pp. 641–49.
- The corresponding theory for the transient Kelvin wakes has further been derived for the Marangoni (Shu, Jian-Jun (2004). "Transient Marangoni waves due to impulsive motion of a submerged body". International Applied Mechanics. 40 (6): 709–14. arXiv:1402.4474. Bibcode:2004IAM....40..709S. doi:10.1023/B:INAM.0000041400.70961.1b.) and free-surface (Shu, Jian-Jun (2006). "Transient free-surface waves due to impulsive motion of a submerged source". Underwater Technology. 26 (4): 133–37. arXiv:1402.4387. doi:10.3723/175605406782725023.) waves.
- The "hull Froude number" (Fr) of a ship is Fr = U / √gL, where U is the ship's speed, g is the acceleration of gravity at the earth's surface, and L is the length of the ship's hull, a characteristic wavelength. See Marc Rabaud and Frédéric Moisy (2013) "Ship wakes: Kelvin or Mach angle?," Physical Review Letters, 110 (21) : 214503. Available on-line at: University of Paris, Sud; Alexandre Darmon, Michael Benzaquen, and Elie Raphaël (2014) "Kelvin wake pattern at large Froude numbers," Journal of Fluid Mechanics, 738 : R3-1–R3-8. Available on-line at: ESPCI ParisTech
- G.B. Whitham (1974). Linear and Nonlinear Waves (John Wiley & Sons Inc., 1974) pp. 409–10 Online scan
- Norwegian University of Science and Technology, "A 127-year-old physics riddle solved", Phys.org, Aug 21, 2019. Retrieved 22 August 2019
- BoatWakes.org, Table of distances
External links
| Look up wake in Wiktionary, the free dictionary. |
| Wikimedia Commons has media related to Wakes (fluids). |


