Van Lamoen circle

In Euclidean plane geometry, the van Lamoen circle is a special circle associated with any given triangle ${\displaystyle T}$. It contains the circumcenters of the six triangles that are defined inside ${\displaystyle T}$ by its three medians.[1][2]

The van Lamoen circle through six circumcenters ${\displaystyle A_{b}}$, ${\displaystyle A_{c}}$, ${\displaystyle B_{c}}$, ${\displaystyle B_{a}}$, ${\displaystyle C_{a}}$, ${\displaystyle C_{b}}$

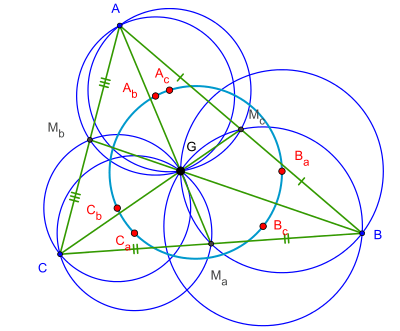
Specifically, let ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ be the vertices of ${\displaystyle T}$, and let ${\displaystyle G}$ be its centroid (the intersection of its three medians). Let ${\displaystyle M_{a}}$, ${\displaystyle M_{b}}$, and ${\displaystyle M_{c}}$ be the midpoints of the sidelines ${\displaystyle BC}$, ${\displaystyle CA}$, and ${\displaystyle AB}$, respectively. It turns out that the circumcenters of the six triangles ${\displaystyle AGM_{c}}$, ${\displaystyle BGM_{c}}$, ${\displaystyle BGM_{a}}$, ${\displaystyle CGM_{a}}$, ${\displaystyle CGM_{b}}$, and ${\displaystyle AGM_{b}}$ lie on a common circle, which is the van Lamoen circle of ${\displaystyle T}$.[2]

History

The van Lamoen circle is named after the mathematician Floor van Lamoen who posed it as a problem in 2000.[3][4] A proof was provided by Kin Y. Li in 2001,[4] and the editors of the Amer. Math. Monthly in 2002.[1][5]

Properties

The center of the van Lamoen circle is point ${\displaystyle X(1153)}$ in Clark Kimberling's comprehensive list of triangle centers.[1]

In 2003, Alexey Myakishev and Peter Y. Woo proved that the converse of the theorem is nearly true, in the following sense: let ${\displaystyle P}$ be any point in the triangle's interior, and ${\displaystyle AA'}$, ${\displaystyle BB'}$, and ${\displaystyle CC'}$ be its cevians, that is, the line segments that connect each vertex to ${\displaystyle P}$ and are extended until each meets the opposite side. Then the circumcenters of the six triangles ${\displaystyle APB'}$, ${\displaystyle APC'}$, ${\displaystyle BPC'}$, ${\displaystyle BPA'}$, ${\displaystyle CPA'}$, and ${\displaystyle CPB'}$ lie on the same circle if and only if ${\displaystyle P}$ is the centroid of ${\displaystyle T}$ or its orthocenter (the intersection of its three altitudes).[6] A simpler proof of this result was given by Nguyen Minh Ha in 2005.[7]

See also

• Parry circle
• Lester circle

References

1. Clark Kimberling (), X(1153) = Center of the van Lemoen circle, in the Encyclopedia of Triangle Centers Accessed on 2014-10-10.
2. Eric W. Weisstein, van Lamoen circle at Mathworld. Accessed on 2014-10-10.
3. Floor van Lamoen (2000), Problem 10830 American Mathematical Monthly, volume 107, page 893.
4. Kin Y. Li (2001), Concyclic problems. Mathematical Excalibur, volume 6, issue 1, pages 1-2.
5. (2002), Solution to Problem 10830. American Mathematical Monthly, volume 109, pages 396-397.
6. Alexey Myakishev and Peter Y. Woo (2003), On the Circumcenters of Cevasix Configuration. Forum Geometricorum, volume 3, pages 57-63.
7. N. M. Ha (2005), Another Proof of van Lamoen's Theorem and Its Converse. Forum Geometricorum, volume 5, pages 127-132.