Trigonometric Rosen–Morse potential

The trigonometric Rosen–Morse potential, named after the physicists Nathan Rosen and Philip M. Morse, is among the exactly solvable quantum mechanical potentials.

Definition

In dimensionless units and modulo additive constants, it is defined as [1]

${\displaystyle V_{tRM}^{(a,b,\lambda )}(\chi )={\frac {a(a-\lambda )}{\sin ^{2}\lambda \chi }}-2b\cot \lambda \chi ,\quad \chi ={\frac {r}{R}},\quad \lambda \chi \in \left[0,\pi \right].}$

(1)

where ${\displaystyle r}$ is a relative distance, ${\displaystyle \lambda }$ is an angle rescaling parameter, and ${\displaystyle R}$ is so far a matching length parameter. Another parametrization of same potential is

${\displaystyle V_{tRM}^{(a,b,\lambda )}(\chi )={\frac {a(a-\lambda )}{\cos ^{2}\lambda \chi }}-2b\tan \lambda \chi ,\quad \chi ={\frac {r}{R}},\quad \lambda \chi \in \left[-{\frac {\pi }{2}},+{\frac {\pi }{2}}\right],}$

(2)

which is the trigonometric version of a one-dimensional hyperbolic potential introduced in molecular physics by Nathan Rosen and Philip M. Morse and given by,[2]

${\displaystyle V(x/d)=B\operatorname {tanh} (x/d)-C\operatorname {sech} ^{2}(x/d),}$

(3)

a parallelism that explains the potential's name. The most prominent application concerns the ${\displaystyle V_{tRM}^{(\ell +1,b,1)}(\chi )}$ parametrization, with ${\displaystyle \ell }$ non-negative integer, and is due to Schrödinger [3] who intended to formulate the hydrogen atom problem on Albert Einstein's closed universe, ${\displaystyle R^{1}\otimes S^{3}}$, the direct product of a time line with a three-dimensional closed space of positive constant curvature, the hypersphere ${\displaystyle S^{3}}$, and introduced it on this geometry in his celebrated equation as the counterpart to the Coulomb potential, a mathematical problem briefly highlighted below.

The ${\displaystyle V_{tRM}^{(\ell +1,0,1)}(\chi )}$ case: Four-dimensional rigid rotator in inertial quantum motion on the three dimensional hypersphere ${\displaystyle S^{3}}$

The hypersphere is a surface in a four-dimensional Euclidean space, ${\displaystyle E_{4}}$, and is defined as,

${\displaystyle x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}=R^{2},}$

(4)

where ${\displaystyle x_{1}}$, ${\displaystyle x_{2}}$, ${\displaystyle x_{3}}$, and ${\displaystyle x_{4}}$ are the Cartesian coordinates of a vector in ${\displaystyle E_{4}}$, and ${\displaystyle R}$ is termed to as hyper-radius. Correspondingly, Laplace operator in ${\displaystyle E_{4}}$ is given by,

${\displaystyle \Delta _{4}(x_{1},x_{2},x_{3},x_{4})={\frac {\partial ^{2}}{\partial x_{4}^{2}}}+{\frac {\partial ^{2}}{\partial x_{1}^{2}}}+{\frac {\partial ^{2}}{\partial x_{2}^{2}}}+{\frac {\partial ^{2}}{\partial x_{3}^{2}}}.}$

(5)

In now switching to polar coordinates,

${\displaystyle {\begin{aligned}x_{4}=R\cos \chi ,\quad x_{3}=R\sin \chi \cos \theta ,\quad \chi ,\theta &\in \left[0,\pi \right],\\x_{2}=R\sin \chi \sin \theta \sin \varphi ,\quad x_{1}=R\sin \chi \sin \theta \cos \varphi ,\quad \varphi &\in \left[0,2\pi \right],\end{aligned}}}$

(6)

one finds the Laplace operator expressed as

${\displaystyle \Delta _{4}(x_{1},x_{2},x_{3},x_{4})\longrightarrow \Delta _{4}(R,\chi ,\theta ,\varphi )={\frac {1}{R^{3}}}{\frac {\partial }{\partial R}}R^{3}{\frac {\partial }{\partial R}}-{\frac {1}{R^{2}}}{\mathcal {K}}^{2}(\chi ,\theta ,\varphi ),}$

(7)

${\displaystyle {\mathcal {K}}^{2}(\chi ,\theta ,\varphi )=-{\frac {1}{\sin ^{2}\chi }}{\frac {\partial }{\partial \chi }}\sin ^{2}\chi {\frac {\partial }{\partial \chi }}+{\frac {{\mathbf {L} }^{2}(\theta ,\varphi )}{\sin ^{2}\chi }}.}$

(8)

Here, ${\displaystyle {\mathcal {K}}^{2}(\chi ,\theta ,\varphi )}$ stands for the squared angular momentum operator in four dimensions, while ${\displaystyle {\mathbf {L} }^{2}(\theta ,\varphi )}$ is the standard three-dimensional squared angular momentum operator. Considering now the hyper-spherical radius ${\displaystyle R}$ as a constant, one encounters the Laplace-Beltrami operator on ${\displaystyle S^{3}}$ as

${\displaystyle \Delta _{S^{3}}(R,\chi ,\theta ,\varphi )=-{\frac {1}{R^{2}}}{\mathcal {K}}^{2}(\chi ,\theta ,\varphi ),\quad R={\mbox{const}}.}$

(9)

With that the free wave equation on ${\displaystyle S^{3}}$ takes the form

${\displaystyle {\begin{aligned}-{\frac {\hbar ^{2}c^{2}}{R^{2}}}\Delta _{S^{3}}(R,\chi ,\theta ,\varphi )Y_{K\ell m}(\chi ,\theta ,\varphi )&={\frac {\hbar ^{2}c^{2}}{R^{2}}}{\mathcal {K}}(\chi ,\theta ,\varphi )Y_{K\ell m}(\chi ,\theta ,\varphi )\\&={\frac {\hbar ^{2}c^{2}}{R^{2}}}K(K+2)Y_{K\ell m}(\chi ,\theta ,\varphi ),\end{aligned}}}$

(10)

${\displaystyle K=0,1,2,...,\quad \ell =0,1,2,...K,\quad |m|=0,1,2,...,\ell .}$

(11)

The solutions, ${\displaystyle Y_{K\ell m}(\chi ,\theta ,\varphi )}$, to this equation are the so-called four-dimensional hyper-spherical harmonics defined as

${\displaystyle Y_{K\ell m}(\chi ,\theta ,\varphi )=\sin ^{\ell }\chi {\mathcal {G}}_{K-\ell }^{\ell +1}(\cos \chi )Y_{\ell }^{m}(\theta ,\varphi ),}$

(12)

where ${\displaystyle {\mathcal {G}}_{n}^{\ell +1}(\cos \chi )}$ are the Gegenbauer polynomials. Changing in (10) variables as

${\displaystyle Y_{K\ell m}(\chi ,\theta ,\varphi )={\frac {\psi _{K\ell }(\chi )}{\sin \chi }}Y_{\ell }(\theta ,\varphi ),}$

(13)

one observes that the ${\displaystyle \psi _{K\ell }(\chi )}$ function satisfies the one-dimensional Schrödinger equation with the ${\displaystyle \csc ^{2}\chi }$ potential according to

${\displaystyle -{\frac {\hbar ^{2}c^{2}}{R^{2}}}\left[{\frac {{\mathrm {d} }^{2}}{{\mathrm {d} }\chi ^{2}}}+{\frac {\ell (\ell +1)}{\sin ^{2}\chi }}\right]\psi _{K\ell }(\chi )={\frac {\hbar ^{2}c^{2}}{R^{2}}}(K+1)^{2}\psi _{K\ell }(\chi ).}$

(14)

The one-dimensional potential in the latter equation, in coinciding with the Rosen–Morse potential in (1) for ${\displaystyle a=\ell +1}$ and ${\displaystyle b=0}$, clearly reveals that for integer ${\displaystyle a}$ values, the first term of this potential takes its origin from the centrifugal barrier on ${\displaystyle S^{3}}$. Stated differently, the equation (10), and its version (14) describe inertial (free) quantum motion of a rigid rotator in the four-dimensional Euclidean space, ${\displaystyle E_{4}}$, such as the H Atom, the positronium, etc. whose "ends" trace the large "circles" (i.e. ${\displaystyle S^{2}}$ spheres) on ${\displaystyle S^{3}}$.

Now the question arises whether the second term in (1) could also be related in some way to the ${\displaystyle S^{3}}$ geometry.

The ${\displaystyle V_{tRM}^{(\ell +1,b,1)}(\chi )}$ case: Electric charge confinement on ${\displaystyle S^{3}}$ and a dipole potential shaped after ${\displaystyle \alpha Z\cot \chi }$

Figure 1: The charge neutrality of the sphere. The lines pouring out of a source placed on the sphere necessarily intersect at the anti-podal point whether or not a real charge of opposite sign is placed there. Consistent formulation of charge-static on the sphere requires a real charge at the anti-podal point and thereby charge-dipoles as fundamental configurations. Consequently, the sphere supports only ${\displaystyle 2^{n}}$ poles with an integer ${\displaystyle n>0}$.

To the amount the cotangent function solves the Laplace–Beltrami equation on ${\displaystyle S^{3}}$,

${\displaystyle \Delta _{S^{3}}(R,\chi ,\theta ,\varphi )\cot \chi =0,}$

(15)

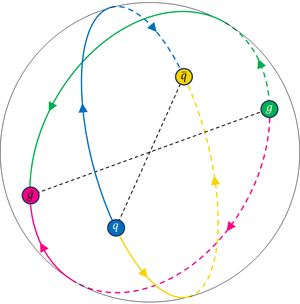
it represents a harmonic function on ${\displaystyle S^{3}}$, a reason for which Schrödinger considered it as the counterpart to the Coulomb potential in flat space, by itself a harmonic function to the ${\displaystyle E_{3}}$ Laplacian. Due to this analogy, the cotangent function is frequently termed to as "curved Coulomb" potential.[4] Such an interpretation ascribes the cotangent potential to a single charge source, and here lies a severe problem. Namely, while open spaces, as is ${\displaystyle E_{3}}$, support single charges, in closed spaces single charge can not be defined in a consistent way.[5] Closed spaces are necessarily and inevitably charge neutral meaning that the minimal fundamental degrees of freedom allowed on them are charge dipoles (see Fig. 1).

For this reason, the wave equation

${\displaystyle {\begin{aligned}-{\frac {\hbar ^{2}c^{2}}{R^{2}}}\left[\Delta _{S^{3}}(R,\chi ,\theta ,\varphi )-2b\cot \chi \right]\Psi _{K\ell m}(\chi ,\theta ,\varphi )&={\frac {\hbar ^{2}c^{2}}{R^{2}}}\left[{\mathcal {K}}^{2}(\chi ,\theta ,\varphi )-2b\cot \chi \right]\Psi _{K\ell m}(\chi ,\theta ,\varphi )\\&={\frac {\hbar ^{2}c^{2}}{R^{2}}}\left[K(K+2)-{\frac {b^{2}}{(K+1)^{2}}}\right]\Psi _{K\ell m}(\chi ,\theta ,\varphi ),\end{aligned}}}$

(16)

which transforms upon the variable change, ${\displaystyle \Psi _{K\ell m}(\chi ,\theta ,\varphi )={\frac {U_{K\ell }^{(b)}(\chi )}{\sin \chi }}Y_{\ell }^{m}(\theta ,\varphi )}$, into the familiar one-dimensional Schrödinger equation with the ${\displaystyle V_{tRM}^{(\ell +1,b,1)}(\chi )}$ trigonometric Rosen–Morse potential,

${\displaystyle -{\frac {\hbar ^{2}c^{2}}{R^{2}}}\left[{\frac {{\mathrm {d} }^{2}}{{\mathrm {d} }\chi ^{2}}}+{\frac {\ell (\ell +1)}{\sin ^{2}\chi }}\right]U_{K\ell }^{(b)}(\chi )-2b\cot \chi U_{K\ell }^{(b)}(\chi )={\frac {\hbar ^{2}c^{2}}{R^{2}}}\left[(K+1)^{2}-{\frac {b^{2}}{(K+1)^{2}}}\right]U_{K\ell }^{(b)}(\chi ),}$

(17)

in reality describes quantum motion of a charge dipole perturbed by the field due to another charge dipole, and not the motion of a single charge within the field produced by another charge. Stated differently, the two equations (16) and (17) do not describe strictly speaking a Hydrogen Atom on ${\displaystyle S_{3}}$, but rather quantum motion on ${\displaystyle S^{3}}$ of a light ${\displaystyle (e^{+},e^{-})}$ dipole perturbed by the dipole potential of another very heavy dipole, like the H Atom, so that the reduced mass, ${\displaystyle \mu }$, would be of the order of the electron mass and could be neglected in comparison with the energy.

In order to understand this decisive issue, one needs to focus attention to the necessity of ensuring validity on ${\displaystyle S^{3}}$ of both the Gauss law and the superposition principle for the sake of being capable to formulate electrostatic there. With the cotangent function in (15) as a single-source potential, such can not be achieved.[6] Rather, it is necessary to prove that the cotangent function represents a dipole potential. Such a proof has been delivered in.[7] To understand the line of arguing of [7] it is necessary to go back to the expression for the Laplace operator in (5) and before considering the hyper-radius as a constant, factorize this space into a time line and ${\displaystyle S^{3}}$. For this purpose, a "time" variable is introduced via the logarithm of the ${\displaystyle S^{3}}$ radius.[8] Introducing this variable change in (7) amounts to the following Laplacian,

${\displaystyle -\left[{\frac {\partial ^{2}}{\partial x_{4}^{2}}}+{\frac {\partial ^{2}}{\partial x_{1}^{2}}}+{\frac {\partial ^{2}}{\partial x_{2}^{2}}}+{\frac {\partial ^{2}}{\partial x_{3}^{2}}}\right]\longrightarrow -\left[{\frac {1}{R^{3}}}{\frac {\partial }{\partial R}}R^{3}{\frac {\partial }{\partial R}}-{\frac {1}{R^{2}}}{\mathcal {K}}^{2}(\chi ,\theta ,\varphi )\right]}$

(18)

${\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \quad \;\;\;{\stackrel {R=e^{\tau }}{\longrightarrow }}-e^{2\tau }\left[{\frac {\partial ^{2}}{\partial \tau ^{2}}}-\left({\mathcal {K}}^{2}(\chi ,\theta ,\varphi )+1\right)\right].}$

(19)

The ${\displaystyle \tau }$ parameter is known as "conformal time", and the whole procedure is referred to as "radial quantization".[8] Charge-static is now built up in setting ${\displaystyle \tau }$=const in (19) and calculating the harmonic function to the remaining piece, the so-called conformal Laplacian, ${\displaystyle \Delta _{S^{3}}^{1}(\chi ,\theta ,\varphi )}$, on ${\displaystyle S^{3}}$, which is read off from (19) as

${\displaystyle \Delta _{S^{3}}^{1}(\tau ,\chi ,\theta ,\varphi )|_{\tau =0}=\Delta _{S^{3}}(R,\chi ,\theta ,\varphi )|_{R=1}+1={\mathcal {K}}^{2}(\chi ,\theta ,\varphi )+1,}$

(20)

where we have chosen ${\displaystyle \tau =0}$, equivalently, ${\displaystyle R=1}$.

Comparison of the latter expression to (15) shows that the correct operator to be employed in the calculation of the harmonic function is not the regular ${\displaystyle S^{3}}$ Laplace–Beltrami operator, ${\displaystyle \Delta _{S^{3}}(R,\chi ,\theta ,\varphi )|_{R=1}}$ but the so-called conformal Laplace–Beltrami operator, ${\displaystyle \Delta _{S^{3}}^{1}(\tau ,\chi ,\theta ,\varphi )|_{\tau =0}=\Delta _{S^{3}}(R,\chi ,\theta ,\varphi )|_{R=1}+1}$ in (20). The Green function to ${\displaystyle \Delta _{S^{3}}^{1}(\tau ,\chi ,\theta ,\varphi )}$ has been calculated for example in.[9] Its values at the respective South and North poles, in turn denoted by ${\displaystyle {\mathcal {G}}_{\pi }(\chi )}$, and ${\displaystyle {\mathcal {G}}_{0}(\chi )}$, are reported as

${\displaystyle {\mathcal {G}}_{\pi }(\chi )=-{\frac {1}{4\pi ^{2}}}\chi \cot \chi ,}$

(21)

${\displaystyle {\mathcal {G}}_{0}(\chi )=-{\frac {1}{4\pi ^{2}}}\left(\chi -\pi \right)\cot \chi ,\quad \chi \in \left[0,\pi \right].}$

(22)

From them one can now construct the dipole potential for a fundamental charge ${\displaystyle {\mathcal {Q}}}$ placed, say, on the North pole, and a fundamental charge of opposite sign, ${\displaystyle -{\mathcal {Q}}}$, placed on the antipodal South pole of ${\displaystyle S^{3}}$. The associated potentials, ${\displaystyle V_{\pi }(\chi )}$ and ${\displaystyle V_{0}(\chi )}$, are then constructed through multiplication of the respective Green function values by the relevant charges [10] as

${\displaystyle V_{\pi }(\chi )=-{\mathcal {Q}}{\mathcal {G}}_{\pi }(\chi )=-{\frac {\left(-{\mathcal {Q}}\right)}{4\pi ^{2}}}\chi \cot \chi ,}$

(23)

${\displaystyle V_{0}(\chi )={\mathcal {Q}}{\mathcal {G}}_{0}(\chi )=-{\frac {\mathcal {Q}}{4\pi ^{2}}}\left(\chi -\pi \right)\cot \chi .}$

(24)

Figure 2: Schematic presentation of the shape of the ${\displaystyle {\underline {C}}}$harge ${\displaystyle {\underline {D}}}$ipole potential ${\displaystyle V_{CD}(\chi )}$ in (25) on ${\displaystyle S^{3}}$. This potential is confining in the sense that with growing distance from the equator, it becomes infinite near the poles, thus preventing the "escape" of the charges, and keeping them "confined" on ${\displaystyle S^{3}}$. Instead, with the decrease of the distances to the equator, it becomes gradually vanishing, and leaves the charges in this region "asymptotically free". In this way, charge-statics on closed spaces provide convenient templates for simulations of confinement phenomena, the most prominent being the confinement of color charges known from the quantum chromodynamics (QCD).

In now assuming validity of the superposition principle, one encounters a Charge Dipole (CD) potential to emerge at a point ${\displaystyle \chi }$ on ${\displaystyle S^{3}}$ according to

${\displaystyle V_{CD}(\chi )=V_{\pi }(\chi )+V_{0}(\chi )=-{\mathcal {Q}}{\mathcal {G}}_{\pi }(\chi )+{\mathcal {Q}}{\mathcal {G}}_{0}(\chi )=-{\frac {\mathcal {Q}}{4\pi }}\cot \chi .}$

(25)

The electric field to this dipole is obtained in the standard way through differentiation as

${\displaystyle E(\chi )=-{\frac {\partial }{\partial \chi }}V_{CD}(\chi )={\frac {\mathcal {Q}}{4\pi }}{\frac {1}{\sin ^{2}\chi }},}$

(26)

and coincides with the precise expression prescribed by the Gauss theorem on ${\displaystyle S^{3}}$, as explained in.[6] Notice that ${\displaystyle {\mathcal {Q}}}$ stands for dimension-less charges. In terms of dimensional charges, ${\displaystyle q}$, related to ${\displaystyle {\mathcal {Q}}}$ via

${\displaystyle {\mathcal {Q}}={\frac {q}{\sqrt {\hbar c}}},}$

(27)

the potential perceived by another charge ${\displaystyle (Zq)/{\sqrt {\hbar c}}}$, is

${\displaystyle V_{CD}(\chi )=-{\frac {q^{2}Z}{4\pi \hbar c}}\cot \chi .}$

(28)

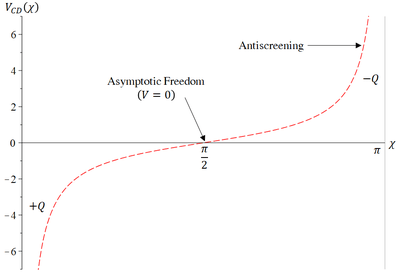
For example, in the case of electrostatic, the fundamental charge ${\displaystyle q}$ is taken the electron charge, ${\displaystyle e}$, in which case the special notation of

${\displaystyle \alpha ={\frac {e^{2}}{4\pi \hbar c}}}$

(29)

is introduced for the so-called fundamental coupling constant of electrodynamics. In effect, one finds

${\displaystyle V_{CD}(\chi )=-\alpha Z\cot \chi .}$

(30)

In Fig. 2 we display the dipole potential ${\displaystyle V_{CD}(\chi )}$ in (30).

With that, the one-dimensional Schrödinger equation that describes on ${\displaystyle S^{3}}$ the quantum motion of an electric charge dipole perturbed by the trigonometric Rosen–Morse potential, produced by another electric charge dipole, takes the form of

${\displaystyle \left(-{\frac {\hbar ^{2}c^{2}}{R^{2}}}{\frac {{\mathrm {d} }^{2}}{{\mathrm {d} }\chi ^{2}}}+V_{\mbox{tRM}}^{(\ell +1,\alpha Z/2,1)}(\chi )\right)U_{K\ell }^{(\alpha Z)}(\chi )={\frac {\hbar ^{2}c^{2}}{R^{2}}}\left({\epsilon }_{\ell n}^{(\alpha Z)}\right)^{2}U_{K\ell }^{(\alpha Z)}(\chi ),}$

(31)

${\displaystyle \qquad \qquad \qquad \qquad \qquad \quad \;\;\,V_{\mbox{tRM}}^{(\ell +1,\alpha Z/2,1)}(\chi )={\frac {\hbar ^{2}c^{2}}{R^{2}}}{\frac {\ell (\ell +1)}{\sin ^{2}\chi }}-2{\frac {\hbar ^{2}c^{2}}{R^{2}}}\alpha Z\cot \chi ,}$

(32)

${\displaystyle \qquad \qquad \qquad \qquad \qquad \quad \;\;{\frac {\hbar ^{2}c^{2}}{R^{2}}}\left(\epsilon _{\ell n}^{(\alpha Z)}\right)^{2}={\frac {\hbar ^{2}c^{2}}{R^{2}}}(K+1)^{2}-{\frac {\hbar ^{2}c^{2}\alpha ^{2}Z^{2}}{4R^{2}(K+1)^{2}}}.}$

(33)

Because of the relationship, ${\displaystyle K-\ell =n}$, with ${\displaystyle n}$ being the node number of the wave function, one could change labeling of the wave functions, ${\displaystyle U_{K\ell }^{(b)}(\chi )}$, to the more familiar in the literature, ${\displaystyle U_{\ell n}^{(b)}(\chi )}$.

In eqs. (31)-(32) one recognizes the one-dimensional wave equation with the trigonometric Rosen–Morse potential in (1) for ${\displaystyle a=\ell +1}$ and ${\displaystyle 2b=\alpha Z}$.

In this way, the cotangent term of the trigonometric Rosen–Morse potential could be derived from the Gauss law on ${\displaystyle S^{3}}$ in combination with the superposition principle, and could be interpreted as a dipole potential generated by a system consisting of two opposite fundamental charges. The centrifugal ${\displaystyle \csc ^{2}\chi }$ term of this potential has been generated by the kinetic energy operator on ${\displaystyle S^{3}}$. In this manner, the complete trigonometric Rosen–Morse potential could be derived from first principles.

Back to Schrödinger's work,[3] the ${\displaystyle S^{3}}$ hyper-radius for the H Atom has turned out to be very big indeed, and of the order of ${\displaystyle 10^{-3}cm}$. This is by eight orders of magnitudes larger than the H Atom size. The result has been concluded from fitting magnetic dipole elements to hydrogen hyper-fine structure effects (see [11]} and reference therein). The aforementioned radius is sufficiently large to allow approximating the hyper-sphere locally by plane space in which case the existence of single charge still could be justified. In cases in which the hyper spherical radius becomes comparable to the size of the system, the charge neutrality takes over. Such an example will be presented in section 6 below.

Before closing this section, it is in order to bring the exact solutions to the equations (31)-(32), given by

${\displaystyle U_{K\ell }^{(\alpha Z)}(\chi )=N_{K\ell }\sin ^{K+1}\chi e^{-{\frac {\alpha Z}{2(K+1)}}}R_{K-\ell }^{{\frac {\alpha Z}{K+1)}},-(K+1)}(\cot \chi ),\quad K-\ell =n,}$

(34)

where ${\displaystyle R_{n}^{\alpha \beta }(x)}$ stand for the Romanovski polynomials.[12] [13] [14]

Application to Coulomb fluids

Coulomb fluids consist of dipolar particles and are modelled by means of direct numerical simulations. It is commonly used to choose cubic cells with periodic boundary conditions in conjunction with Ewald summation techniques. In a more efficient alternative method pursued by,[15][16] one employs as a simulation cell the hyper spherical surface ${\displaystyle S^{3}}$ in (4). As already mentioned above, the basic object on ${\displaystyle S^{3}}$ is the electric charge dipole, termed to as "bi-charge" in fluid dynamics, which can be visualized classically as a rigid "dumbbell" (rigid rotator) of two antipodal charges of opposite signs, ${\displaystyle +q}$ and ${\displaystyle -q}$. The potential of a bi-charge is calculated by solving on ${\displaystyle S_{3}}$ the Poisson equation,

${\displaystyle \Delta _{S^{3}}(\chi )V_{\mbox{b-ch}}(\chi )=-{\frac {4\pi q}{R^{3}}}\left[\delta _{S^{3}}(\chi ,\chi _{0})-\delta _{S_{3}}(\chi ,{\bar {\chi }}_{0})\right].}$

(35)

Here, ${\displaystyle \chi _{0}}$ is the angular coordinate of a charge ${\displaystyle q}$ placed at angular position ${\displaystyle \chi _{0}}$, read off from the North pole, while ${\displaystyle {\bar {\chi }}_{0}}$ stands for the anti-podal to ${\displaystyle \chi _{0}}$ angular coordinate of the position, at which the charge of opposite signs is placed in the Southern hemisphere. The solution found,

${\displaystyle V_{\mbox{b-ch}}(\chi )={\frac {q}{R}}\cot \chi ,}$

(36)

equals the potential in (30), modulo conventions regarding the charge signs and units. It provides an alternative proof to that delivered by the equations (19)-(30) of the fact that the cotangent function on ${\displaystyle S^{3}}$ has to be associated with the potential generated by a charge dipole. In contrast, the potentials in the above equations (23), and (24), have been interpreted in [15] as due to so called single "pseudo-charge" sources, where a "pseudo-charge" is understood as the association of a point charge ${\displaystyle q}$ with a uniform neutralizing background of a total charge, ${\displaystyle -q}$.

Application to color confinement and the physics of quarks

The confining nature of the cotangent potential in (28) finds an application in a phenomenon known from the physics of strong interaction which refers to the non-observability of free quarks, the constituents of the hadrons. Quarks are considered to possess three fundamental internal degree of freedom, conditionally termed to as "colors", red ${\displaystyle (r)}$, blue ${\displaystyle (b)}$, and green ${\displaystyle (g)}$, while anti-quarks carry the corresponding anti-colors, anti-red ${\displaystyle ({\bar {r}})}$, anti-blue ${\displaystyle ({\bar {b}})}$, or anti-green ${\displaystyle ({\bar {g}})}$, meaning that the non-observability of free quarks is equivalent to the non-observability of free color-charges, and thereby to the "color neutrality" of the hadrons. Quark "colors" are the fundamental degrees of freedom of the Quantum Chromodynamics (QCD), the gauge theory of strong interaction. In contrast to the Quantum Electrodynamics, the gauge theory of the electromagnetic interactions, QCD is a non-Abelian theory which roughly means that the "color" charges, denoted by ${\displaystyle g_{s}(Q^{2})}$, are not constants, but depend on the values, ${\displaystyle Q^{2}}$, of the transferred momentum, giving rise to the so-called, running of the strong coupling constant, ${\displaystyle \alpha _{s}(Q^{2})}$, in which case the Gauss law becomes more involved.[17] However, at low momentum transfer, near the so-called infrared regime, the momentum dependence of the color charge significantly weakens,[18] and in starting approaching a constant value,

Figure 3: Schematic presentation of the internal meson structure.

Figure 4: The mass distributions of the ${\displaystyle f_{0}}$ mesons with spin and CP parities calculated by the aids of ${\displaystyle V_{tRM}^{(\ell +1,\alpha _{s}N_{c}/2,1)}(\chi )}$ and the mass formula in eq. (33) modulo the replacement of ${\displaystyle \alpha Z}$ by ${\displaystyle \alpha _{s}N_{c}}$.

${\displaystyle g_{s}(Q^{2}){\stackrel {Q^{2}\to 0}{\longrightarrow }}{\mbox{const}},}$

(37)

drives the Gauss law back to the standard form known from Abelian theories. For this reason, under the condition of color charge constancy, one can attempt to model the color neutrality of hadrons in parallel to the neutrality of Coulomb fluids, namely, by considering quantum color motions on closed surfaces. In particular for the case of the hyper-sphere ${\displaystyle S^{3}}$, it has been shown in,[19] that a potential, there denoted by ${\displaystyle V_{CCD}(\chi )}$, and obtained from the one in (28) through the replacement,

${\displaystyle \alpha Z\longrightarrow \alpha _{s}N_{c},\quad \alpha _{s}={\frac {g_{s}^{2}}{4\pi }},}$

(38)

i.e. the potential

${\displaystyle V_{CCD}(\chi )=-\alpha _{s}N_{c}\cot \chi ,}$

(39)

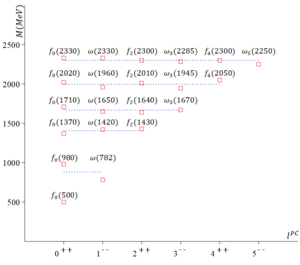
where ${\displaystyle N_{c}}$ is the number of colors, is the adequate one for the description of the spectra of the light mesons with masses up to ${\displaystyle \sim 2500MeV}$. Especially, the hydrogen like degeneracies have been well captured. This because the potential, in being a harmonic function to the Laplacian on ${\displaystyle S^{3}}$, has same symmetry as the Laplacian by itself, a symmetry that is defined by the isometry group of ${\displaystyle S^{3}}$, i.e. by ${\displaystyle SO(4)}$, the maximal compact group of the conformal group ${\displaystyle SO(2,4)}$. For this reason, the potential in (39), as part of ${\displaystyle V_{tRM}^{(\ell +1,\alpha _{s}N_{c}/2,1)}(\chi )}$, accounts not only for color confinement, but also for conformal symmetry in the infrared regime of QCD. Within such a picture, a meson is constituted by a quark ${\displaystyle (q)}$-anti-quark ${\displaystyle ({\bar {q}})}$ color dipole in quantum motion on an ${\displaystyle S^{3}}$ geometry, and gets perturbed by the dipole potential in (39), generated by and other color dipole, such as a gluon ${\displaystyle (g)}$-anti-gluon ${\displaystyle ({\bar {g}})}$, as visualized in Fig. 3.

The ${\displaystyle S^{3}}$ geometry could be viewed as the unique closed space-like geodesic of a four-dimensional hyperboloid of one sheet, ${\displaystyle {\mathbf {H} }_{1}^{4}}$, foliating outside of the causal Minkowski light-cone the space-like region, assumed to have one more spatial dimension, this in accord with the so-called de Sitter Special Relativity, ${\displaystyle dS_{4}}$.[20] Indeed, potentials, in being instantaneous and not allowing for time orderings, represent virtual, i.e. acausal processes and as such can be generated in one-dimensional wave equations upon proper transformations of virtual quantum motions on surfaces located outside the causal region marked by the Light Cone. Such surfaces can be viewed as geodesics of the surfaces foliating the space like region. Quantum motions on open ${\displaystyle {\mathbf {H} }_{1}^{4}}$ geodesics can give rise to barriers describing resonances transmitted through them.[7] An illustrative example for the application of the color confining dipole potential in (39) to meson spectroscopy is given in Fig. 4. It should be pointed out that the potentials in the above equations (23) and (24) have been alternatively derived in,[21][22] from Wilson loops with cusps, predicting their magnitude as ${\displaystyle \alpha _{s}N_{c}/(4\pi ^{2})}$, and in accord with (38).

The potential in (39) has furthermore been used in [23] in the Dirac equation on ${\displaystyle S^{3}}$, and has been shown to predict realistic electromagnetic nucleon form-factors and related constants such as mean square electric-charge and magnetic-dipole radii, proton and nucleon magnetic dipole moments and their ratio, etc.

Applicability of ${\displaystyle V_{tRM}^{\left(\ell +1,b,1\right)}}$ to phase transitions

The property of the trigonometric Rosen-Morse potential, be it in the parametrization with ${\displaystyle b=\alpha Z/2}$ in eq. (32) which is of interest to electrodynamics, or in the ${\displaystyle b=\alpha _{s}N_{c}/2}$ parametrization of interest to QCD from the previous section, qualifies it to studies of phase transitions in systems with electromagnetic or strong interactions on hyperspherical "boxes" of finite volumes [24] .[25] The virtue of such studies lies in the possibility to express the temperature, ${\displaystyle T}$, as the inverse, ${\displaystyle T=1/R}$, to the radius ${\displaystyle R}$ of the hypersphere. For this purpose, knowledge on the partition function (statistical mechanics), here denoted by ${\displaystyle {\mathcal {Z}}(R,b)}$, of the potential under consideration is needed. In the following we evaluate ${\displaystyle {\mathcal {Z}}(R,b)}$ for the case of the Schrödinger equation on ${\displaystyle S^{3}}$ with linear energy (here in units of MeV),

${\displaystyle {\begin{aligned}-{\Big (}{\frac {\hbar ^{2}c^{2}}{2\mu c^{2}R^{2}}}\Delta _{S^{3}}(R,\chi ,\theta ,\varphi )|_{\theta =\pi /2,\varphi =0}&-2b{\frac {\hbar c}{R}}\cot \chi {\Big )}\psi (\chi )=E_{K}\psi (\chi ),\\E_{K}={\frac {\hbar ^{2}c^{2}}{2\mu c^{2}R^{2}}}(K+1)^{2}&-{\frac {\hbar c}{R}}{\frac {b^{2}}{(K+1)^{2}}},\end{aligned}}}$

(40)

where ${\displaystyle \mu c^{2}}$ is the reduced mass of the two-body system under consideration. The partition function (statistical mechanics) for this energy spectrum is defined in the standard way as,

${\displaystyle {\begin{aligned}{\mathcal {Z}}(R,b)&=\sum _{K=0}^{K=\infty }(K+1)^{2}e^{-\beta \left(E_{K}-E_{0}\right)}\\&=1+e^{\beta E_{0}}\sum _{K=1}^{K=\infty }(K+1)^{2}e^{-\beta E_{K}}.\end{aligned}}}$

(41)

Here, the thermodynamic beta is defined as ${\displaystyle \beta =(k_{B}T)^{-1}}$ with ${\displaystyle k_{B}}$ standing for the Boltzmann constant. In evaluating ${\displaystyle {\mathcal {Z}}(R,b)}$ it is useful to recall that with the increase of ${\displaystyle K}$ the second term on the right hand side in (40) becomes negligible compared to the term proportional ${\displaystyle (K+1)^{2}}$, a behavior which becomes even more pronounced for the choices, ${\displaystyle 2b=\alpha Z}$, and ${\displaystyle 2b=\alpha _{s}N_{c}}$. In both cases ${\displaystyle b}$ is much smaller compared to the corresponding dimensionless factor, ${\displaystyle (\hbar c)/(2\mu c^{2}R)}$, multiplying ${\displaystyle (\hbar c/R)(K+1)^{2}}$. For this reason the partition function under investigation might be well approximated by,

${\displaystyle {\begin{aligned}{\mathcal {Z}}(R,b)&=\sum _{K=0}^{K=\infty }(K+1)^{2}e^{-\beta \left(E_{K}-E_{0}\right)}\\&=1+e^{-\beta \left(E_{1}-E_{0}\right)}+e^{\beta E_{0}}\sum _{K=2}^{K=\infty }(K+1)^{2}e^{-\beta E_{K}}\\&\approx 1+e^{-\beta \left(E_{1}-E_{0}\right)}+e^{\beta E_{0}}\int _{0}^{\infty }x^{2}e^{-ax^{2}}{\mathrm {d} }x\\&=1+e^{-\beta \left(E_{1}-E_{0}\right)}+e^{\beta E_{0}}{\frac {\sqrt {\pi }}{4(a)^{\frac {3}{2}}}},\quad a=\beta {\frac {\hbar ^{2}c^{2}}{2\mu c^{2}R^{2}}}.\end{aligned}}}$

(42)

Along same lines, the partition function for the ${\displaystyle b=\alpha Z/2}$ parametrization corresponding to the Hydrogen atom on ${\displaystyle S^{3}}$ has been calculated in,[26] where a more sophisticated approximation has been employed. When transcribed to the current notations and units, the partition function in [26] presents itself as,

${\displaystyle {\begin{aligned}{\mathcal {Z}}\left(R,{\frac {\alpha Z}{2}}\right)\approx 1+e^{\beta E_{0}}\int _{0}^{\infty }x^{2}e^{-ax^{2}+{\frac {p}{x^{2}}}},\quad p=\beta {\frac {\hbar c}{R}}\alpha ^{2}Z^{2}.\end{aligned}}}$

(43)

The infinite integral has first been treated by means of partial integration giving,

${\displaystyle {\begin{aligned}\int _{0}^{\infty }x^{2}e^{-ax^{2}+{\frac {p}{x^{2}}}}&=\int _{0}^{\infty }x^{2}e^{-ax^{2}}e^{\frac {p}{x^{2}}}{\mathrm {d} }x\\&=-{\frac {1}{2a}}\int _{0}^{\infty }xe^{\frac {p}{x^{2}}}{\mathrm {d} }e^{-ax^{2}}\\&=-{\frac {1}{2a}}xe^{\frac {p}{x^{2}}}e^{-ax^{2}}|_{0}^{\infty }+{\frac {1}{2a}}\int _{0}^{\infty }e^{-ax^{2}}{\mathrm {d} }\,\left(xe^{\frac {p}{x^{2}}}\right)\\&={\frac {1}{2a}}\int _{0}^{\infty }e^{-ax^{2}+{\frac {p}{x^{2}}}}{\mathrm {d} }x+{\frac {2p}{2a}}\int _{0}^{\infty }e^{-ax^{2}+{\frac {p}{x^{2}}}}{\mathrm {d} }\left({\frac {1}{x}}\right).\end{aligned}}}$

(44)

Then the argument of the exponential under the sign of the integral has been cast as,

${\displaystyle {\begin{aligned}-ax^{2}+{\frac {p}{x^{2}}}=-z^{2}+2i{\sqrt {ap}},\quad z={\sqrt {a}}x+i{\frac {\sqrt {p}}{x}},\end{aligned}}}$

(45)

thus reaching the following intermediate result,

${\displaystyle {\begin{aligned}{\mathcal {Z}}\left(R,{\frac {\alpha Z}{2}}\right)\approx 1+{\frac {1}{2a}}e^{\beta E_{0}}e^{2i{\sqrt {ap}}}\int _{0}^{\infty }e^{-z^{2}}{\mathrm {d} }\left(x+{\frac {2p}{x}}\right).\end{aligned}}}$

(46)

As a next step the differential has been represented as

${\displaystyle {\begin{aligned}x+{\frac {2p}{x}}={\frac {1}{2}}\left({\frac {1}{\sqrt {a}}}-2i{\sqrt {p}}\right)z+{\frac {1}{2}}\left({\frac {1}{\sqrt {a}}}+2i{\sqrt {p}}\right)z^{\ast },\end{aligned}}}$

(47)

an algebraic manipulation which allows to express the partition function in (46) in terms of the ${\displaystyle {\mbox{erf}}(u)}$ function of complex argument according to,

${\displaystyle {\begin{aligned}{\mathcal {Z}}\left(R,{\frac {\alpha Z}{2}}\right)\approx 1+{\frac {1}{4a}}e^{\beta E_{0}}\times \left[\left({\frac {1}{\sqrt {a}}}-2i{\sqrt {p}}\right)e^{2i{\sqrt {ap}}}\int _{\Gamma }e^{-z^{2}}{\mathrm {d} }z+\left({\frac {1}{\sqrt {a}}}+2i{\sqrt {p}}\right)e^{-2i{\sqrt {ap}}}\int _{\Gamma }e^{-\left(z^{\ast }\right)^{2}}{\mathrm {d} }z^{\ast }\right],\\\end{aligned}}}$

(48)

where ${\displaystyle \Gamma }$ is an arbitrary path on the complex plane starting in zero and ending in ${\displaystyle u\to \infty }$. For more details and physical interpretations, see.[26]

See also

• Romanovski polynomials
• Pöschl–Teller potential

References

1. Cooper, F.; Khare, A.; Sukhatme, U. P. (2001). Supersymmetry in Quantum Mechanics. Singapore: World Scientific. ISBN 978-9-81-024612-9.
2. Rosen, N.; Morse, P. M. (1932). "On the Vibrations of Polyatomic Molecules". Phys. Rev. 42 (2): 210. Bibcode:1932PhRv...42..210R. doi:10.1103/PhysRev.42.210.
3. Schrödinger, E. (1941). "The Factorization of the Hypergeometric Equation". Proc. Roy. Irish Acad. A. 47: 53–54. JSTOR 20488434.
4. Barut, A. O.; Wilson, R. (1985). "On the dynamical group of the kepler problem in a curved space of constant curvature". Phys. Lett. A. 110 (7–8): 351. Bibcode:1985PhLA..110..351B. doi:10.1016/0375-9601(85)90052-0.
5. Landau, L. D.; Lifschitz, E. M. (1971). The Classical Theory of Fields. Vol. 2 of Course of Theoretical Physics (3rd. ed.). Pergamon Press. p. 335. ISBN 978-0-08-016019-1.
6. Pouria, P. (2010). "Modification of Coulomb's law in closed spaces". Am. J. Phys. 78 (4): 403. arXiv:0912.0225. Bibcode:2010AmJPh..78..403P. doi:10.1119/1.3272020.
7. Kirchbach, M.; Compean, C. B. (2016). "Modelling duality between bound and resonant meson spectra by means of free quantum motions on the de Sitter space-time ${\displaystyle dS_{4}}$". Eur. Phys. J. A. 52 (7): 210. arXiv:1608.05041. Bibcode:2016EPJA...52..210K. doi:10.1140/epja/i2016-16210-3.
8. Fubini, S.; Hanson, A. J.; Jackiw, R. (1973). "New Approach to Field Theory". Phys. Rev. D. 7 (6): 1732. Bibcode:1973PhRvD...7.1732F. doi:10.1103/PhysRevD.7.1732.
9. Alertz, B. (1990). "Electrodynamics in Robertson-Walker spacetimes" (PDF). Ann. Inst. Henri Poincaré. 53 (3): 319.
10. Kellogg, O. D. (1953). Foundations of Potential Theory. New York: Dover. ISBN 978-0-48-660144-1.
11. Bessis, N.; Bessis, G.; Shamseddine, R. (1982). "Atomic fine structure in a space of constant curvature". J. Phys. A: Math. Gen. 15 (10): 3131. Bibcode:1982JPhA...15.3131B. doi:10.1088/0305-4470/15/10/017.
12. Romanovski, V. (1929). "Sur quelques classes nouvelles de polynomes orthogonaux". C. R. Acad. Sci. Paris (in French). 188: 1023.
13. Routh, E. J. (1884). "On some properties of certain solutions of a differential equation of second order". Proc. London Math. Soc. 16: 245. doi:10.1112/plms/s1-16.1.245.
14. Raposo, A. P.; Weber, H. J.; Álvarez Castillo, D. E.; Kirchbach, M. (2007). "Romanovski polynomials in selected physics problems". Cent. Eur. J. Phys. 5 (3): 253–284. arXiv:0706.3897. Bibcode:2007CEJPh...5..253R. doi:10.2478/s11534-007-0018-5.
15. Caillol, J. M. (1993). "A new potential for the numerical simulations of electrolyte solutions on a hypersphere". J. Chem. Phys. 99 (11): 8953. Bibcode:1993JChPh..99.8953C. doi:10.1063/1.465565.
16. Caillol, J. M.; Trulsson, M. (2014). "A new dipolar potential for numerical simulations of polar fluids on the 4D hypersphere". J. Chem. Phys. 141 (12): 124111. arXiv:1407.7739. Bibcode:2014JChPh.141l4111C. doi:10.1063/1.4896181. PMID 25273416.
17. Serna, M.; Cahill, K. (2003). "Riemannian gauge theory and charge quantization". Journal of High Energy Physics. 2003 (10): 054. arXiv:hep-th/0205250. Bibcode:2003JHEP...10..054S. doi:10.1088/1126-6708/2003/10/054.
18. Deur, A.; Burkert, V.; Chen, J. P.; Korsch, W. (2008). "Determination of the effective strong coupling constant ${\displaystyle \alpha _{s,g_{1}}\left(Q^{2}\right)}$ from CLAS spin structure function data". Phys. Lett. B. 665 (5): 349–351. arXiv:0803.4119. Bibcode:2008PhLB..665..349D. doi:10.1016/j.physletb.2008.06.049.
19. Kirchbach, M.; Compean, C. B. (2017). "Addendum to: Modelling duality between bound and resonant meson spectra by means of free quantum motions on the de Sitter space-time ${\displaystyle dS_{4}}$". Eur. Phys. J. A. 53 (4): 65. Bibcode:2017EPJA...53...65K. doi:10.1140/epja/i2017-12269-6.
20. Aldrovandi, R.; Beltrán Almeida, J. P.; Pereira, J. G. (2007). "de Sitter special relativity". Class. Quantum Grav. 24 (6): 1385–1404. arXiv:gr-qc/0606122. Bibcode:2007CQGra..24.1385A. doi:10.1088/0264-9381/24/6/002.
21. Belitsky, A. V.; Gorsky, A. S.; Korchemsky, G. P. (2003). "Gauge/string duality for QCD conformal operators". Nucl. Phys. B. 667 (1–2): 3–54. arXiv:hep-th/0304028. Bibcode:2003NuPhB.667....3B. doi:10.1016/S0550-3213(03)00542-X.
22. Gorsky, A. S. (2005). "Spin chains and gauge-string duality". Theor. Math. Phys. 142 (2): 153. arXiv:hep-th/0308182. doi:10.1007/s11232-005-0042-9.
23. Kirchbach, M.; Compean, C. B. (2018). "Proton's electromagnetic form factors from a non-power confinement potential". Nucl. Phys. A. 980: 32. arXiv:1810.03665. Bibcode:2018NuPhA.980...32K. doi:10.1016/j.nuclphysa.2018.09.083.
24. Aharony, O.; Marsano, J.; Minwalla, S.; Papadodimas, K.; Van Raamsdonk, M. (2004). "The Hagedorn deconfinement phase transition in weakly coupled large N gauge theories". Adv. Theor. Math. Phys. 8 (4): 603–696. arXiv:hep-th/0310285. doi:10.4310/ATMP.2004.v8.n4.a1.
25. Hands, S.; Hollowood, T. J.; Myers, J. C. (2010). "QCD with Chemical Potential in a Small Hyperspherical Box". Journal of High Energy Physics. 2010 (7): 86. arXiv:1003.5813. Bibcode:2010JHEP...07..086H. doi:10.1007/JHEP07(2010)086.
26. Blinder, S. M. (1996). "Canonical partition function for the hydrogen atom in curved space". J. Math. Chem. 19: 43. doi:10.1007/BF01165129. hdl:2027.42/43064.