Trapezo-rhombic dodecahedron

In geometry, the trapezo-rhombic dodecahedron or rhombo-trapezoidal dodecahedron is a convex dodecahedron with 6 rhombic and 6 trapezoidal faces. It has D_3h symmetry. A concave form can be constructed with an identical net, seen as excavating trigonal trapezohedra from the top and bottom.

Trapezo-rhombic dodecahedron
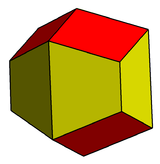Convex and concave
Type	Plesiohedron Johnson solid dual
Faces	6 rhombus, 6 trapezoid
Edges	24
Vertices	14
Vertex configuration	(2) 4.4.4 (6) 4.4.4.4 (6) 4.4.4
Symmetry	D_3h, [3,2], (*322), order 12
Rotation symmetry	D₃, [3,2]⁺, (322), order 6
Dual polyhedron	Triangular orthobicupola
Properties	convex
Net	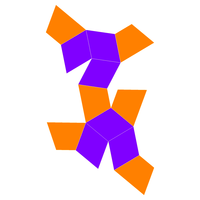(click to enlarge)

Construction

This polyhedron could be constructed by taking a tall uniform hexagonal prism, and making 3 angled cuts on the top and bottom. The trapezoids represent what remains of the original prism sides, and the 6 rhombi a result of the top and bottom cuts.

Space-filling tessellation

A space-filling tessellation, the trapezo-rhombic dodecahedral honeycomb, can be made by translated copies of this cell. Each "layer" is a hexagonal tiling, or a rhombille tiling, and alternate layers are connected by shifting their centers and rotating each polyhedron so the rhombic faces match up.

:

In the special case that the long sides of the trapezoids equals twice the length of the short sides, the solid now represents the 3D Voronoi cell of a sphere in a Hexagonal Close Packing (HCP), next to Face-Centered-Cubic an optimal way to stack spheres in a lattice. It is therefore similar to the rhombic dodecahedron, which can be represented by turning the lower half of the picture at right over an angle of 60 degrees. The rhombic dodecahedron is a Voronoi cell of the other optimal way to stack spheres.

As the Voronoi cell of a regular space pattern, it is a plesiohedron. It is the polyhedral dual of the triangular orthobicupola.

Variations

The trapezo-rhombic dodecahedron can be seen as an elongation of another dodecahedron, which can be called a rhombo-triangular dodecahedron, with 6 rhombi (or squares) and 6 triangles. It also has d_3h symmetry and is space-filling. It has 21 edges and 11 vertices. With square faces it can be seen as a cube split across the 3-fold axis, separated with the two halves rotated 180 degrees, and filling the gaps with triangles. When used as a space-filler, connecting dodecahedra on their triangles leaves two cubical step surfaces on the top and bottom which can connect with complementary steps.

gollark: Epicbot has been insulting me for much of the day.

gollark: https://github.com/jbangert/trapcc

gollark: Oh yes, I heard of that.

gollark: It lets you parameterize modules over types, or something confusing like that.

gollark: ~~copy rust's in its entirety~~

References

Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. p. 170. ISBN 0-486-23729-X.
Mathematical Recreations and Essays Walter William Rouse Ball, Harold Scott Macdonald Coxeter, p.151
Structure in Nature Is a Strategy for Design, Peter Jon Pearce, p.48 Spacefilling systems based on rhombic dodecahedron

External links

Weisstein, Eric W. "Space-filling polyhedron". MathWorld.
VRML model

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.