Tic-tac-toe variants

Tic-tac-toe is an instance of an m,n,k-game, where two players alternate taking turns on an m×n board until one of them gets k in a row.[1] Harary's generalized tic-tac-toe is an even broader generalization. The game can also be generalized as a n^d game.[2] The game can be generalised even further from the above variants by playing on an arbitrary hypergraph where rows are hyperedges and cells are vertices.

A complete game of Notakto, a misère variant of the game

Many board games share the element of trying to be the first to get n-in-a-row, including three men's morris, nine men's morris, pente, gomoku, Qubic, Connect Four, Quarto, Gobblet, Order and Chaos, Toss Across, and Mojo.

Variants of tic-tac-toe date back several millennia.[3]

Historic

An early variation of tic-tac-toe was played in the Roman Empire, around the first century BC.[4] It was called Terni Lapilli and instead of having any number of pieces, each player only had three, thus they had to move them around to empty spaces to keep playing. The game's grid markings have been found chalked all over Rome.[5] However, according to Claudia Zaslavsky's book Tic Tac Toe: And Other Three-In-A Row Games from Ancient Egypt to the Modern Computer, Tic-tac-toe could be traced back to ancient Egypt.[6][7] Another closely related ancient game is three men's morris which is also played on a simple grid and requires three pieces in a row to finish.[8]

Variants in higher dimensions

3D Tic-tac-toe

Main article: 3D tic-tac-toe

3-dimensional tic-tac-toe on a 3×3×3 board. In this game, the first player has an easy win by playing in the centre if 2 people are playing.

One can play on a board of 4x4 squares, winning in several ways. Winning can include: 4 in a straight line, 4 in a diagonal line, 4 in a diamond, or 4 to make a square. Another variant, Qubic, is played on a 4×4×4 board; it was solved by Oren Patashnik in 1980 (the first player can force a win).[9] Higher-dimensional variations are also possible.[10]

Misère games

Misere Tic-tac-toe

In misère tic-tac-toe, the player wins if the opponent gets n in a row.[11][12][13][14] This game is also known as avoidance tic tac toe,[12] toe-tac-tic,[12][15] inverse tic tac toe,[13] or reverse tic tac toe.[14] A 3×3 game is a draw. More generally, the first player can draw or win on any board (of any dimension) whose side length is odd, by playing first in the central cell and then mirroring the opponent's moves.[10][13]

Notakto

Notakto is a misere and impartial form of tic tac toe. This means unlike in misere tic tac toe, in Notakto, both players play as the same symbol, X.[16] It also can be played on one or multiple boards.[17]

Variants with bigger boards

Quixo

The game Quixo is played on a 5 by 5 board of cubes with two players or teams.[18] On a player's turn, they select a blank cube or a cube with their symbol on it that is at the edge of the board. If a blank cube was selected, the cube is turned to be the player's symbol (either a X or O). The game ends when one player gets 5 in a row.[18][19][20][21]

Unrestricted n-in-a-row

Unrestricted n-in-a-row is played on an infinite tic-tac-toe board where the goal is for one player to get n in a row.[2]

Isomorphic games

Number Scrabble

There is a game that is isomorphic to tic-tac-toe, but on the surface appears completely different. It is called Pick15[22] or Number Scrabble.[23] Two players in turn say a number between one and nine. A particular number may not be repeated. The game is won by the player who has said three numbers whose sum is 15.[22][24] If all the numbers are used and no one gets three numbers that add up to 15 then the game is a draw.[22] Plotting these numbers on a 3×3 magic square shows that the game exactly corresponds with tic-tac-toe, since three numbers will be arranged in a straight line if and only if they total 15.[25]

Word Tic-tac-toe

	eat	bee	less	→e
	air	bits	lip	→i
	soda	book	lot	→o
↙ s	↓ a	↓ b	↓ l	↘   t

Another isomorphic game uses a list of nine carefully chosen words, for instance "eat", "bee", "less", "air", "bits", "lip", "soda", "book", and "lot". Each player picks one word in turn and to win, a player must select three words with the same letter. The words may be plotted on a tic-tac-toe grid in such a way that a three in a row line wins.[26]

Other variants

Numerical Tic-tac-toe

Numerical Tic Tac Toe is a variation invented by the mathematician Ronald Graham.[27] The numbers 1 to 9 are used in this game. The first player plays with the odd numbers, the second player plays with the even numbers. All numbers can be used only once. The player who puts down 15 points in a line wins (sum of 3 numbers).[28] This game can be generalized to a n × n board.[28]

Check Lines

In the 1970s, there was a two player game made by Tri-ang Toys & Games called Check Lines, in which the board consisted of eleven holes arranged in a geometrical pattern of twelve straight lines each containing three of the holes. Each player had exactly five tokens and played in turn placing one token in any of the holes. The winner was the first player whose tokens were arranged in two lines of three (which by definition were intersecting lines). If neither player had won by the tenth turn, subsequent turns consisted of moving one of one's own tokens to the remaining empty hole, with the constraint that this move could only be from an adjacent hole.[29]

Quantum tic-tac-toe

Quantum tic tac toe allows players to place a quantum superposition of numbers on the board, i.e. the players' moves are "superpositions" of plays in the original classical game. This variation was invented by Allan Goff of Novatia Labs.[30]

A complete game of Wild tic-tac-toe.

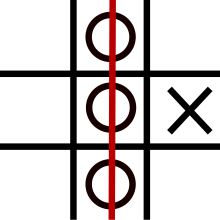
Wild tic-tac-toe

In wild tic-tac-toe, players can choose to place either X or O on each move.[7][31][32][33] It can be played as a normal game where the player who makes three in a row wins or a misere game where they would lose.[7] This game is also called your-choice tic-tac-toe[34] or Devil's tic-tac-toe.

SOS

In the game SOS, the players on each turn choose to play a "S" or an "O" in an empty square.[35] If a player creates the sequence, SOS vertically, horizontally or diagonally they get a point and also take another turn.[36] The player with the most points (SOSs) is the winner.[35][36]

Treblecross

A completed game of Treblecross

In Treblecross, both players play with the same symbol (a X[13] or black chip[37]). The game is played on a 1 by n board with k equal to 3.[13] The player who creates a three in a row of X's (or black chips) wins the game.[13][37]

Revenge n-in-a-row

In revenge n-in-a-row, the player who creates a n-in-a-row wins unless the opponent can create a n-in-a-row in the next move where they lose.[38][13]

Random turn tic-tac-toe

In the game, random turn tic-tac-toe, a coin flip determines whose turn it is.[7]

Quick Tic-tac-toe

In quick-tac-toe, on each turn the players can play their mark in any squares they want provided that all the marks are in the same vertical or horizontal row. The winner is the player who places the last mark.[39]

Ultimate tic-tac-toe

In ultimate tic-tac-toe, the board is composed of nine tic-tac-toe boards arranged in a 3-by-3 grid. Players take turns playing in the smaller tic-tac-toe boards until one of them wins in the larger tic-tac-toe board.

References

1. Pham, Duc-Nghia; Park, Seong-Bae (2014-11-12). PRICAI 2014: Trends in Artificial Intelligence: 13th Pacific Rim International Conference on Artificial Intelligence, PRICAI 2014, Gold Coast, QLD, Australia, December 1-5, 2014, Proceedings. Springer. ISBN 9783319135601. Archived from the original on 2017-08-23.
2. Beck, József (2008). Combinatorial Games: Tic-Tac-Toe Theory. Cambridge University Press. ISBN 9780521461009.
3. Epstein, Richard A. (2014-06-28). The Theory of Gambling and Statistical Logic, Revised Edition. Gulf Professional Publishing. ISBN 9780080571843. Archived from the original on 2016-12-21.
4. Kisačanin, Branislav; Gelautz, Margrit (2014-11-26). Advances in Embedded Computer Vision. Springer. ISBN 9783319093871. Archived from the original on 2017-11-30.
5. "Roman Board Games -- Terni Lapilli". www.aerobiologicalengineering.com. Archived from the original on 2016-12-01. Retrieved 2016-12-03.
6. Zaslavsky, Claudia (1982). Tic Tac Toe: And Other Three-In-A Row Games from Ancient Egypt to the Modern Computer. Crowell. ISBN 0-690-04316-3.
7. Epstein, Richard A. (2012-12-28). The Theory of Gambling and Statistical Logic. Academic Press. ISBN 9780123978707. Archived from the original on 2017-11-30.
8. Canisius College – Morris Games Archived 2013-03-13 at the Wayback Machine
9. Oren Patashnik, "Qubic: 4 x 4 x 4 Tic-Tac-Toe", Mathematical Magazine 53 (1980) 202–216.
10. Golomb, Solomon W.; Hales, Alfred W. (2002), "Hypercube tic-tac-toe", More games of no chance (Berkeley, CA, 2000), Math. Sci. Res. Inst. Publ., 42, Cambridge: Cambridge Univ. Press, pp. 167–182, MR 1973012.
11. Averbach, Bonnie; Chein, Orin (1980), Problem Solving Through Recreational Mathematics, Dover, p. 252, ISBN 9780486131740, archived from the original on 2016-08-04.
12. "Tic-tac-toe (Math Lair)". mathlair.allfunandgames.ca. Archived from the original on 2016-12-20. Retrieved 2016-12-03.
13. Ma, Wei Ji. "Generalized Tic-tac-toe". www.weijima.com. Archived from the original on 2017-11-30. Retrieved 2016-12-11.
14. Armstrong, Tricia (2016-12-18). The Whole-Brain Solution: Thinking Tools to Help Students Observe, Make Connections and Solve Problems. Pembroke Publishers Limited. ISBN 9781551381565. Archived from the original on 2017-11-30.
15. Silverman, David L. (1991). Your Move: Logic, Math and Word Puzzles for Enthusiasts. Courier Corporation. ISBN 9780486267319.
16. Cram, Scott. "How to Play and Win Notakto". Archived from the original on 2016-11-25. Retrieved 2016-12-02.
17. Cram, Scott. "Secrets of Nim (Notakto)". Archived from the original on 2016-11-25. Retrieved 2016-12-12.
18. "Quixo (R)". www.math.uaa.alaska.edu. Archived from the original on 2015-09-04. Retrieved 2016-12-18.
19. "Quixo - Games - Galapemy". www.galapemy.com. Archived from the original on 2016-12-20. Retrieved 2016-12-18.
20. "Quixio" (PDF). Archived (PDF) from the original on September 8, 2014. Retrieved December 18, 2016.
21. Golladay, Sonja Musser (2007-01-01). Los Libros de Acedrex Dados E Tablas: Historical, Artistic and Metaphysical Dimensions of Alfonso X's "Book of Games". ProQuest. ISBN 9780549274346. Archived from the original on 2017-02-15.
22. Juul, Jesper (2011-08-19). Half-Real: Video Games Between Real Rules and Fictional Worlds. MIT Press. ISBN 9780262516518. Archived from the original on 2017-11-30.
23. Michon, John A. (1967-01-01). "The Game of JAM: An Isomorph of Tic-Tac-Toe". The American Journal of Psychology. 80 (1): 137–140. doi:10.2307/1420555. JSTOR 1420555.
24. "TicTacToe Magic" (PDF). Archived (PDF) from the original on December 20, 2016. Retrieved December 17, 2016.
25. "Oh Boy! I Get to do Math!: Tic-Tac-Toe as a Magic Square". Oh Boy! I Get to do Math!. 2015-05-30. Archived from the original on 2016-12-21. Retrieved 2016-12-17.
26. Schumer, Peter D. (2004), Mathematical Journeys, John Wiley & Sons, pp. 71–72, ISBN 9780471220664, archived from the original on 2016-08-04.
27. Markowsky, George. "Numerical Tic-Tac-Toe" (PDF). Archived (PDF) from the original on December 20, 2016. Retrieved December 3, 2016.
28. Sandlund, Bryce; Staley, Kerrick; Dixon, Michael; Butler, Steve. "Numerical Tic-Tac-Toe on the 4 × 4 Board" (PDF). Archived (PDF) from the original on 2016-10-20.
29. Check Lines Archived 2016-03-04 at the Wayback Machine, BoardGameGeek, retrieved 2013-09-13.
30. Goff, Allan (November 2006). "Quantum tic-tac-toe: A teaching metaphor for superposition in quantum mechanics". American Journal of Physics. College Park, MD: American Association of Physics Teachers. 74 (11): 962–973. doi:10.1119/1.2213635. ISSN 0002-9505.
31. "Puzzles in Education - Wild Tic-Tac-Toe". puzzles.com. Archived from the original on 2016-11-04. Retrieved 2016-11-29.
32. Mendelson, Elliott (2016-02-03). Introducing Game Theory and its Applications. CRC Press. ISBN 9781482285871. Archived from the original on 2017-11-30.
33. "Variations of Tic Tac Toe" (PDF). Retrieved December 3, 2016.
34. "Camp Games". americanriverresort.com. Archived from the original on 2016-12-20. Retrieved 2016-12-12.
35. Harrelson, Angie (2007-07-01). Patterns - Literature, Arts, and Science. Prufrock Press Inc. ISBN 9781593632618. Archived from the original on 2016-12-21.
36. "SoS Game". SlideME. Archived from the original on 2016-12-20. Retrieved 2016-12-04.
37. Mendelson, Elliott (2004-07-03). Introducing Game Theory and its Applications. CRC Press. ISBN 9781584883005.
38. W., Weisstein, Eric. "Tic-Tac-Toe". mathworld.wolfram.com. Archived from the original on 2016-12-10. Retrieved 2016-12-12.
39. Silverman, David L. (1991-01-01). Your Move: Logic, Math and Word Puzzles for Enthusiasts. Courier Corporation. ISBN 9780486267319.