Square packing in a square

Square packing in a square is a packing problem where the objective is to determine how many squares of side one (unit squares) can be packed into a square of side ${\displaystyle a}$. If ${\displaystyle a}$ is an integer, the answer is ${\displaystyle a^{2}}$, but the precise, or even asymptotic, amount of wasted space for non-integer ${\displaystyle a}$ is an open question.[1]

Unsolved problem in mathematics: What is the asymptotic growth rate of wasted space for square packing in a half-integer square? (more unsolved problems in mathematics)

Small numbers of squares

5 unit squares in a square of side length ${\displaystyle 2+1/{\sqrt {2}}\approx 2.707}$

10 unit squares in a square of side length ${\displaystyle 3+1/{\sqrt {2}}\approx 3.707}$

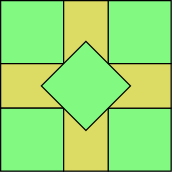
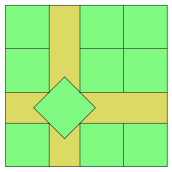
The smallest value of ${\displaystyle a}$ that allows the packing of ${\displaystyle n}$ unit squares is known when ${\displaystyle n}$ is a perfect square (in which case it is ${\displaystyle {\sqrt {n}}}$), as well as for ${\displaystyle n={}}$2, 3, 5, 6, 7, 8, 10, 13, 14, 15, 24, 34, 35, 46, 47, and 48. For most of these numbers (with the exceptions only of 5 and 10), the packing is the natural one with axis-aligned squares, and ${\displaystyle a}$ is ${\displaystyle \lceil {\sqrt {n}}\rceil }$.[2][3] The figure shows the optimal packings for 5 and 10 squares, the two smallest numbers of squares for which the optimal packing involves tilted squares.[4][5]

The smallest unresolved case involves packing 11 unit squares into a larger square. 11 unit squares cannot be packed in a square of side less than ${\displaystyle \textstyle 2+2{\sqrt {4/5}}\approx 3.789}$. By contrast, the tightest known packing of 11 squares is inside a square of side length approximately 3.877084, slightly improving a similar packing found earlier by Walter Trump.[6]

Asymptotic results

For larger values of the side length ${\displaystyle a}$, the exact number of unit squares that can pack an ${\displaystyle a\times a}$ square remains unknown. It is always possible to pack a ${\displaystyle \lfloor a\rfloor \times \lfloor a\rfloor }$ grid of axis-aligned unit squares, but this may leave a large area, approximately ${\displaystyle 2a(a-\lfloor a\rfloor )}$, uncovered and wasted.[4] Instead, Paul Erdős and Ronald Graham showed that for a different packing by tilted unit squares, the wasted space could be significantly reduced to ${\displaystyle o(a^{7/11})}$ (here written in little o notation).[7] In an unpublished manuscript, Graham and Fan Chung further reduced the wasted space, to ${\displaystyle O(a^{3/5})}$.[8] However, as Klaus Roth and Bob Vaughan proved, all solutions must waste space at least ${\displaystyle \Omega {\bigl (}a^{1/2}(a-\lfloor a\rfloor ){\bigr )}}$. In particular, when ${\displaystyle a}$ is a half-integer, the wasted space is at least proportional to its square root.[9] The precise asymptotic growth rate of the wasted space, even for half-integer side lengths, remains an open problem.[1]

Some numbers of unit squares are never the optimal number in a packing. In particular, if a square of size ${\displaystyle a\times a}$ allows the packing of ${\displaystyle n^{2}-2}$ unit squares, then it must be the case that ${\displaystyle a\geq n}$ and that a packing of ${\displaystyle n^{2}}$ unit squares is also possible.[2]

See also

• Circle packing in a square
• Squaring the square

References

1. Brass, Peter; Moser, William; Pach, János (2005), Research Problems in Discrete Geometry, New York: Springer, p. 45, ISBN 978-0387-23815-9, MR 2163782
2. Kearney, Michael J.; Shiu, Peter (2002), "Efficient packing of unit squares in a square", Electronic Journal of Combinatorics, 9 (1), Research Paper 14, 14 pp., MR 1912796.
3. Bentz, Wolfram (2010), "Optimal packings of 13 and 46 unit squares in a square", Electronic Journal of Combinatorics, 17 (1), Research Paper 126, MR 2729375
4. Friedman, Erich (2009), "Packing unit squares in squares: a survey and new results", Electronic Journal of Combinatorics, Dynamic Survey 7, MR 1668055.
5. Stromquist, Walter (2003), "Packing 10 or 11 unit squares in a square", Electronic Journal of Combinatorics, 10, Research Paper 8, MR 2386538.
6. Gensane, Thierry; Ryckelynck, Philippe (2005), "Improved dense packings of congruent squares in a square", Discrete & Computational Geometry, 34 (1): 97–109, doi:10.1007/s00454-004-1129-z, MR 2140885
7. Erdős, P.; Graham, R. L. (1975), "On packing squares with equal squares" (PDF), Journal of Combinatorial Theory, Series A, 19: 119–123, doi:10.1016/0097-3165(75)90099-0, MR 0370368.
8. • Chung, Fan; Graham, Ron, Efficient packings of unit squares in a large square (PDF), retrieved 2019-04-28
9. Roth, K. F.; Vaughan, R. C. (1978), "Inefficiency in packing squares with unit squares", Journal of Combinatorial Theory, Series A, 24 (2): 170–186, doi:10.1016/0097-3165(78)90005-5, MR 0487806.

External links

• Squares in Squares, Erich's Packing Center, Erich Friedman, Stetson University