Spherical pendulum

In physics, a spherical pendulum is a higher dimensional analogue of the pendulum. It consists of a mass m moving without friction on the surface of a sphere. The only forces acting on the mass are the reaction from the sphere and gravity.

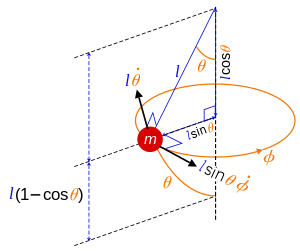
Spherical pendulum: angles and velocities.

Owing to the spherical geometry of the problem, spherical coordinates are used to describe the position of the mass in terms of (r, θ, φ), where r is fixed. In what follows l is the constant length of the pendulum, so r = l.

Lagrangian mechanics

Main article: Lagrangian mechanics

The Lagrangian is [1]

${\displaystyle L={\frac {1}{2}}mr^{2}\left({\dot {\theta }}^{2}+\sin ^{2}\theta \ {\dot {\phi }}^{2}\right)+mgr\cos \theta .}$

The Euler–Lagrange equations give :

${\displaystyle {\frac {d}{dt}}\left(mr^{2}{\dot {\theta }}\right)-mr^{2}\sin \theta \cos \theta {\dot {\phi }}^{2}+mgr\sin \theta =0}$

and

${\displaystyle {\frac {d}{dt}}\left(mr^{2}\sin ^{2}\theta \,{\dot {\phi }}\right)=0}$

showing that angular momentum is conserved.

The conical pendulum refers to the special solutions where ${\displaystyle {\dot {\theta }}=0}$ and ${\displaystyle {\dot {\phi }}}$ is a constant not depending on time.

Hamiltonian mechanics

Main article: Hamiltonian mechanics

The Hamiltonian is

${\displaystyle H=P_{\theta }{\dot {\theta }}+P_{\phi }{\dot {\phi }}-L}$

where

${\displaystyle P_{\theta }={\frac {\partial L}{\partial {\dot {\theta }}}}=mr^{2}{\dot {\theta }}}$

and

${\displaystyle P_{\phi }={\frac {\partial L}{\partial {\dot {\phi }}}}=mr^{2}{\dot {\phi }}\sin ^{2}\theta }$

See also

• Conical Pendulum
• Newton's three laws of motion
• Pendulum
• Pendulum (mathematics)
• Routhian mechanics

References

1. Landau, Lev Davidovich; Evgenii Mikhailovich Lifshitz (1976). Course of Theoretical Physics: Volume 1 Mechanics. Butterworth-Heinenann. pp. 33–34. ISBN 0750628960.

• Weinstein, Alexander (1942). "The spherical pendulum and complex integration". The American Mathematical Monthly. 49 (8): 521–523. doi:10.1080/00029890.1942.11991275.
• Kohn, Walter (1946). "Countour integration in the theory of the spherical pendulum and the heavy symmetrical top". Transactions of the American Mathematical Society. 59 (1): 107–131. doi:10.2307/1990314. JSTOR 1990314.
• Olsson, M. G. (1981). "Spherical pendulum revisited". American Journal of Physics. 49 (6): 531–534. Bibcode:1981AmJPh..49..531O. doi:10.1119/1.12666.
• Horozov, Emil (1993). "On the isoenergetical non-degeneracy of the spherical pendulum". Physics Letters A. 173 (3): 279–283. Bibcode:1993PhLA..173..279H. doi:10.1016/0375-9601(93)90279-9.
• Shiriaev, A. S.; Ludvigsen, H.; Egeland, O. (2004). "Swinging up the spherical pendulum via stabilizatio of its first integrals". Automatica. 40: 73–85. doi:10.1016/j.automatica.2003.07.009.
• Essen, Hanno; Apazidis, Nicholas (2009). "Turning points of the spherical pendulum and the golden ration". European Journal of Physics. 30 (2): 427–432. Bibcode:2009EJPh...30..427E. doi:10.1088/0143-0807/30/2/021.
• Dullin, Holger R. (2013). "Semi-global symplectic invariants of the spherical pendulum". Journal of Differential Equations. 254 (7): 2942–2963. doi:10.1016/j.jde.2013.01.018.