Sextic equation

In algebra, a sextic (or hexic) polynomial is a polynomial of degree six. A sextic equation is a polynomial equation of degree six—that is, an equation whose left hand side is a sextic polynomial and whose right hand side is zero. More precisely, it has the form:

${\displaystyle ax^{6}+bx^{5}+cx^{4}+dx^{3}+ex^{2}+fx+g=0,\,}$

Graph of a sextic function, with 6 real roots (crossings of the x axis) and 5 critical points. Depending on the number and vertical locations of minima and maxima, the sextic could have 6, 4, 2, or no real roots. The number of complex roots equals 6 minus the number of real roots.

where a ≠ 0 and the coefficients a, b, c, d, e, f, g may be integers, rational numbers, real numbers, complex numbers or, more generally, members of any field.

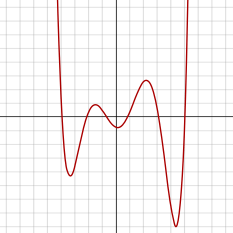
A sextic function is a function defined by a sextic polynomial. Because they have an even degree, sextic functions appear similar to quartic functions when graphed, except they may possess an additional local maximum and local minimum each. The derivative of a sextic function is a quintic function.

Since a sextic function is defined by a polynomial with even degree, it has the same infinite limit when the argument goes to positive or negative infinity. If the leading coefficient a is positive, then the function increases to positive infinity at both sides and thus the function has a global minimum. Likewise, if a is negative, the sextic function decreases to negative infinity and has a global maximum.

Solvable sextics

Some sixth degree equations, such as ax⁶ + dx³ + g = 0, can be solved by factorizing into radicals, but other sextics cannot. Évariste Galois developed techniques for determining whether a given equation could be solved by radicals which gave rise to the field of Galois theory.[1]

It follows from Galois theory that a sextic equation is solvable in term of radicals if and only if its Galois group is contained either in the group of order 48 which stabilizes a partition of the set of the roots into three subsets of two roots or in the group of order 72 which stabilizes a partition of the set of the roots into two subsets of three roots.

There are formulas to test either case, and, if the equation is solvable, compute the roots in term of radicals.[2]

The general sextic equation can be solved in terms of Kampé de Fériet functions.[1] A more restricted class of sextics can be solved in terms of generalised hypergeometric functions in one variable using Felix Klein's approach to solving the quintic equation.[1]

Examples

Watt's curve, which arose in the context of early work on the steam engine, is a sextic in two variables.

One method of solving the cubic equation involves transforming variables to obtain a sextic equation having terms only of degrees 6, 3, and 0, which can be solved as a quadratic equation in the cube of the variable.

Etymology

The describer "sextic" comes from the Latin prefix for 6 or 6th ("sexa-"), and the Greek suffix meaning "pertaining to" ("-tic"). The much less common "hexic" uses Greek for both its prefix ("hex-") and its suffix ("-ic"). In both cases, the prefix refers to the degree of the function. Often, these type of functions will simply be referred to as "6th degree functions".

See also

• Cayley's sextic
• Cubic function
• Septic equation

References

1. Mathworld - Sextic Equation
2. T. R. Hagedorn, General formulas for solving solvable sextic equations, J. Algebra 233 (2000), 704-757