7-limit tuning

7-limit or septimal tunings and intervals are musical instrument tunings that have a limit of seven: the largest prime factor contained in the interval ratios between pitches is seven. Thus, for example, 50:49 is a 7-limit interval, but 14:11 is not.

Harmonic seventh Play , septimal seventh.
Septimal chromatic semitone on C Play .
9/7 major third from C to E [1] Play . This, "extremely large third," may resemble a neutral third or blue note.[2]
Septimal minor third on C Play .

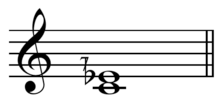
For example, the greater just minor seventh, 9:5 Play  is a 5-limit ratio, the harmonic seventh has the ratio 7:4 and is thus a septimal interval. Similarly, the septimal chromatic semitone, 21:20, is a septimal interval as 21÷7=3. The harmonic seventh is used in the barbershop seventh chord and music. (Play ) Compositions with septimal tunings include La Monte Young's The Well-Tuned Piano, Ben Johnston's String Quartet No. 4, and Lou Harrison's Incidental Music for Corneille's Cinna.

The Great Highland Bagpipe is tuned to a ten-note seven-limit scale:[3] 1:1, 9:8, 5:4, 4:3, 27:20, 3:2, 5:3, 7:4, 16:9, 9:5.

In the 2nd century Ptolemy described the septimal intervals: 7/4, 8/7, 7/6, 12/7, 7/5, and 10/7.[4] Those considering 7 to be consonant include Marin Mersenne,[5] Giuseppe Tartini, Leonhard Euler, François-Joseph Fétis, J. A. Serre, Moritz Hauptmann, Alexander John Ellis, Wilfred Perrett, Max Friedrich Meyer.[4] Those considering 7 to be dissonant include Gioseffo Zarlino, René Descartes, Jean-Philippe Rameau, Hermann von Helmholtz, A. J. von Öttingen, Hugo Riemann, Colin Brown, and Paul Hindemith ("chaos"[6]).[4]

Lattice and tonality diamond

The 7-limit tonality diamond:

7/4
3/27/5
5/46/57/6
1/11/11/11/1
8/55/312/7
4/310/7
8/7

This diamond contains four identities (1, 3, 5, 7 [P8, P5, M3, H7]). Similarly, the 2,3,5,7 pitch lattice contains four identities and thus 3-4 axes, but a potentially infinite number of pitches. LaMonte Young created a lattice containing only identities 3 and 7, thus requiring only two axes, for The Well-Tuned Piano.

Approximation using equal temperament

It is possible to approximate 7-limit music using equal temperament, for example 31-ET.

FractionCentsDegree (31-ET)Name (31-ET)
1/100.0C
8/72316.0D or E
7/62676.9D♯
6/53168.2E♭
5/438610.0E
4/349812.9F
7/558315.0F♯
10/761716.0G♭
3/270218.1G
8/581421.0A♭
5/388422.8A
12/793324.1A or B
7/496925.0A♯
2/1120031.0C
gollark: It's going slowly because programming is hard and I'm lazy and conflicted on some design aspects.
gollark: Minoteaur (v2.0.0 really early alpha) is a server-rendered webapp using SQLite/Node.js/Express. I briefly experimented with making UI-type stuff run on the client but it was annoying.
gollark: On the one hand that encourages non-stateful backends (using the database and FS for storage and not holding important stuff in RAM), which I do anyway, but on the others it's inefficient and annoying.
gollark: I like Node.js/Express for my random bodging because it's less evil than PHP (especially when type checked), has really great libraries available, and doesn't do the silly (conventional for PHP) "one execution of your script per request" thing.
gollark: On the PHP thing, popular does not mean or imply good.

See also

Sources
  1. Fonville, John. "Ben Johnston's Extended Just Intonation- A Guide for Interpreters", p.112, Perspectives of New Music, Vol. 29, No. 2 (Summer, 1991), pp. 106-137.
  2. Fonville (1991), p.128.
  3. Benson, Dave (2007). Music: A Mathematical Offering, p.212. ISBN 9780521853873.
  4. Partch, Harry (2009). Genesis of a Music: An Account of a Creative Work, Its Roots, and Its Fulfillments, p.90-1. ISBN 9780786751006.
  5. Shirlaw, Matthew (1900). Theory of Harmony, p.32. ISBN 978-1-4510-1534-8.
  6. Hindemith, Paul (1942). Craft of Musical Composition, v.1, p.38. ISBN 0901938300.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.