Gamma scale
The γ (gamma) scale is a non-octave repeating musical scale invented by Wendy Carlos while preparing Beauty in the Beast (1986) though it does not appear on the album. It is derived from approximating just intervals using multiples of a single interval without, as is standard in equal temperaments, requiring an octave (2:1). It may be approximated by splitting the perfect fifth (3:2) into 20 equal parts (3:21⁄20≈35.1 cents), by splitting the neutral third into two equal parts, or ten equal parts of approximately 35.1 cents each (![]()
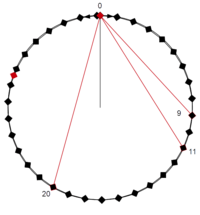
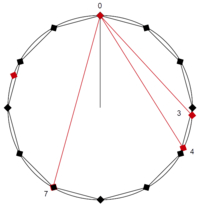
The scale step may also precisely be derived from using 20:11 (B↓, 1035 cents, ![]()
![]()
and (![]()
"It produces nearly perfect triads."[3] "A 'third flavor,' sort of intermediate to 'alpha' and 'beta', although a melodic diatonic scale is easily available."[1]
| interval name | size (steps) |
size (cents) |
just ratio |
just (cents) |
error |
| minor third | 9 | 315.89 | 6:5 | 315.64 | +0.25 |
| major third | 11 | 386.09 | 5:4 | 386.31 | −0.22 |
| perfect fifth | 20 | 701.98 | 3:2 | 701.96 | +0.02 |
See also
- Alpha scale
- Beta scale
- Delta scale
- Bohlen–Pierce scale
- Gamma chord
Sources
- Carlos, Wendy (1989–96). "Three Asymmetric Divisions of the Octave", WendyCarlos.com.
- Benson, Dave (2006). Music: A Mathematical Offering, p.232-233. ISBN 0-521-85387-7. "Carlos has 34.188 γ-scale degrees to the octave, corresponding to a scale degree of 35.1 cents."
- Milano, Dominic (November 1986). "A Many-Colored Jungle of Exotic Tunings", Keyboard.


