Schwarz alternating method

In mathematics, the Schwarz alternating method or alternating process is an iterative method introduced in 1869-1870 by Hermann Schwarz in the theory of conformal mapping. Given two overlapping regions in the complex plane in each of which the Dirichlet problem could be solved, Schwarz described an iterative method for solving the Dirichlet problem in their union, provided their intersection was suitably well behaved. This was one of several constructive techniques of conformal mapping developed by Schwarz as a contribution to the problem of uniformization, posed by Riemann in the 1850s and first resolved rigorously by Koebe and Poincaré in 1907. It furnished a scheme for uniformizing the union of two regions knowing how to uniformize each of them separately, provided their intersection was topologically a disk or an annulus. From 1870 onwards Carl Neumann also contributed to this theory.

In the 1950s Schwarz's method was generalized in the theory of partial differential equations to an iterative method for finding the solution of an elliptic boundary value problem on a domain which is the union of two overlapping subdomains. It involves solving the boundary value problem on each of the two subdomains in turn, taking always the last values of the approximate solution as the next boundary conditions. It is used in numerical analysis, under the name multiplicative Schwarz method (in opposition to additive Schwarz method) as a domain decomposition method.

History
DDM original logo: representation of the problem considered by H. A. Schwarz in 1870. The blue rectangle was originally a square

It was first formulated by H. A. Schwarz [1] and served as a theoretical tool: its convergence for general second order elliptic partial differential equations was first proved much later, in 1951, by Solomon Mikhlin.[2]

The algorithm

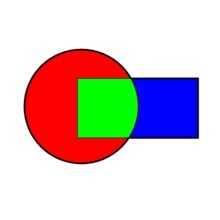
The original problem considered by Schwarz was a Dirichlet problem (with the Laplace's equation) on a domain consisting of a circle and a partially overlapping square. To solve the Dirichlet problem on one of the two subdomains (the square or the circle), the value of the solution must be known on the border: since a part of the border is contained in the other subdomain, the Dirichlet problem must be solved jointly on the two subdomains. An iterative algorithm is introduced:

  1. Make a first guess of the solution on the circle's boundary part that is contained in the square
  2. Solve the Dirichlet problem on the circle
  3. Use the solution in (2) to approximate the solution on the square's boundary
  4. Solve the Dirichlet problem on the square
  5. Use the solution in (4) to approximate the solution on the circle's boundary, then go to step (2).

At convergence, the solution on the overlap is the same when computed on the square or on the circle.

Optimized Schwarz methods

The convergence speed depends on the size of the overlap between the subdomains, and on the transmission conditions (boundary conditions used in the interface between the subdomains). It is possible to increase the convergence speed of the Schwarz methods by choosing adapted transmission conditions: theses methods are then called Optimized Schwarz methods.[3]

gollark: You want the KristPay plugin.
gollark: all > php
gollark: I have a vague idea how, I just really can't be bothered and don't want to encourage this sort of thing.
gollark: No, it can do that sort of thing natively.
gollark: Not exactly.

See also

Notes
  1. See his paper (Schwarz 1870b)
  2. See the paper (Mikhlin 1951): a comprehensive exposition was given by the same author in later books
  3. Gander, Martin J.; Halpern, Laurence; Nataf, Frédéric (2001), "Optimized Schwarz Methods", 12th International Conference on Domain Decomposition Methods (PDF)

References

Original papers

Conformal mapping and harmonic functions

  • Nevanlinna, Rolf (1939), "Über das alternierende Verfahren von Schwarz", J. Reine Angew. Math., 180: 121–128
  • Nevanlinna, Rolf (1939), "Bemerkungen zum alternierenden Verfahren", Monatshefte für Mathematik und Physik, 48: 500–508, doi:10.1007/bf01696203
  • Nevanlinna, Rolf (1953), Uniformisierung, Die Grundlehren der Mathematischen Wissenschaften in Einzeldarstellungen mit besonderer Berücksichtigung der Anwendungsgebiete, 64, Springer
  • Sario, Leo (1953), "Alternating method on arbitrary Riemann surfaces", Pacific J. Math., 3 (3): 631–645, doi:10.2140/pjm.1953.3.631
  • Morgenstern, Dietrich (1956), "Begründung des alternierenden Verfahrens durch Orthogonalprojektion", Z. Angew. Math. Mech., 36 (7–8): 255–256, doi:10.1002/zamm.19560360711, hdl:10338.dmlcz/100409
  • Cohn, Harvey (1980), Conformal mapping on Riemann surfaces, Dover, pp. 242–262, ISBN 0-486-64025-6, Chapter 12, Alternating Procedures
  • Garnett, John B.; Marshall, Donald E. (2005), Harmonic Measure, Cambridge University Press, ISBN 1139443097
  • Freitag, Eberhard (2011), Complex analysis. 2. Riemann surfaces, several complex variables, abelian functions, higher modular functions, Springer, ISBN 978-3-642-20553-8
  • de Saint-Gervais, Henri Paul (2016), Uniformization of Riemann Surfaces: revisiting a hundred-year-old theorem, translated by Robert G. Burns, European Mathematical Society, doi:10.4171/145, ISBN 978-3-03719-145-3, translation of French text
  • Chorlay, Renaud (2007), L'émergence du couple local-global dans les théories géométriques, de Bernhard Riemann à la théorie des faisceaux (PDF), pp. 123–134 (cited in de Saint-Gervais)
  • Bottazzini, Umberto; Gray, Jeremy (2013), Hidden Harmony—Geometric Fantasies: The Rise of Complex Function Theory, Sources and Studies in the History of Mathematics and Physical Sciences, Springer, ISBN 978-1461457251

PDEs and numerical analysis

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.