Right conoid
In geometry, a right conoid is a ruled surface generated by a family of straight lines that all intersect perpendicularly to a fixed straight line, called the axis of the right conoid.
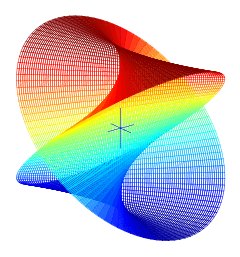
A right conoid as a ruled surface.
Using a Cartesian coordinate system in three-dimensional space, if we take the z-axis to be the axis of a right conoid, then the right conoid can be represented by the parametric equations:
where h(u) is some function for representing the height of the moving line.
Examples
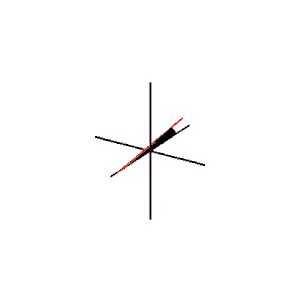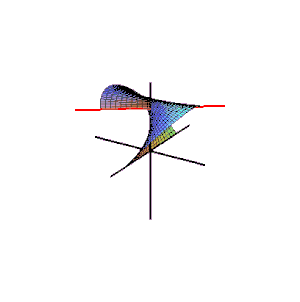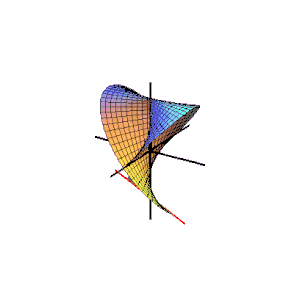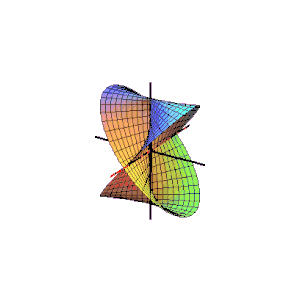
Generation of a typical right conoid
A typical example of right conoids is given by the parametric equations
The image on the right shows how the coplanar lines generate the right conoid.
Other right conoids include:
- Helicoid:
- Whitney umbrella:
- Wallis's conical edge:
- Plücker's conoid:
- hyperbolic paraboloid: (with x-axis and y-axis as its axes).
gollark: Hmm, "satan 2.0" is still ahead in the auction.
gollark: Unfortunately, HTech™ bad engines™ continue to generate additional web standards.
gollark: Fortunately, we were able to neutralize them.
gollark: Briefly.
gollark: Do those even work nowadays?
See also
External links
- "Conoid", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Right Conoid from MathWorld.
- Plücker's conoid from MathWorld
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.