Quantum jump method

The quantum jump method, also known as the Monte Carlo wave function (MCWF) method, is a technique in computational physics used for simulating open quantum systems and quantum dissipation. The quantum jump method was developed by Dalibard, Castin and Mølmer, with a very similar method also developed by Carmichael in the same time frame. Other contemporaneous works on wave-function-based Monte Carlo approaches to open quantum systems include those of Dum, Zoller and Ritsch and Hegerfeldt and Wilser.[1][2]

Method
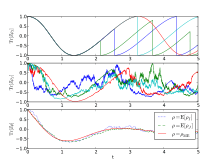
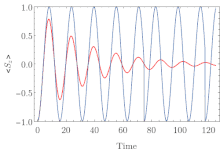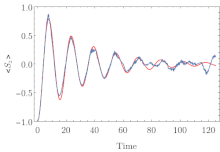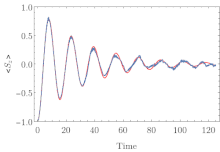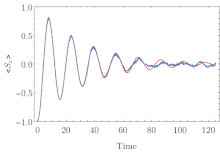
An example of the quantum jump method being used to approximate the density matrix of a two-level atom undergoing damped Rabi oscillations. The random jumps can clearly be seen in the top subplot, and the bottom subplot compares the fully simulated density matrix to the approximation obtained using the quantum jump method.
Animation of the Monte Carlo prediction (blue) for the population of a coherently-driven, damped two-level system as more trajectories are added to the ensemble average, compared to the master equation prediction (red).

The quantum jump method is an approach which is much like the master-equation treatment except that it operates on the wave function rather than using a density matrix approach. The main component of the method is evolving the system's wave function in time with a pseudo-Hamiltonian; where at each time step, a quantum jump (discontinuous change) may take place with some probability. The calculated system state as a function of time is known as a quantum trajectory, and the desired density matrix as a function of time may be calculated by averaging over many simulated trajectories. For a Hilbert space of dimension N, the number of wave function components is equal to N while the number of density matrix components is equal to N2. Consequently, for certain problems the quantum jump method offers a performance advantage over direct master-equation approaches.[1]


gollark: Thanks!
gollark: Wait, WHAT?!
gollark: Yes, go.
gollark: nXg5XAR in about 20 seconds.
gollark: ToD xx:25:11, AR at xx:23:11, I'll post the code when it's time.

References
  1. Mølmer, K.; Castin, Y.; Dalibard, J. (1993). "Monte Carlo wave-function method in quantum optics". Journal of the Optical Society of America B. 10 (3): 524. Bibcode:1993JOSAB..10..524M. doi:10.1364/JOSAB.10.000524.
  2. The associated primary sources are, respectively:
    • Dalibard, Jean; Castin, Yvan; Mølmer, Klaus (February 1992). "Wave-function approach to dissipative processes in quantum optics". Physical Review Letters. 68 (5): 580–583. arXiv:0805.4002. Bibcode:1992PhRvL..68..580D. doi:10.1103/PhysRevLett.68.580. PMID 10045937.
    • Carmichael, Howard (1993). An Open Systems Approach to Quantum Optics. Springer-Verlag. ISBN 978-0-387-56634-4.
    • Dum, R.; Zoller, P.; Ritsch, H. (1992). "Monte Carlo simulation of the atomic master equation for spontaneous emission". Physical Review A. 45 (7): 4879–4887. Bibcode:1992PhRvA..45.4879D. doi:10.1103/PhysRevA.45.4879. PMID 9907570.
    • Hegerfeldt, G. C.; Wilser, T. S. (1992). "Ensemble or Individual System, Collapse or no Collapse: A Description of a Single Radiating Atom". In H.D. Doebner; W. Scherer; F. Schroeck, Jr. (eds.). Classical and Quantum Systems (PDF). Proceedings of the Second International Wigner Symposium. World Scientific. pp. 104–105.

Further reading
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.