Pseudo-deltoidal icositetrahedron
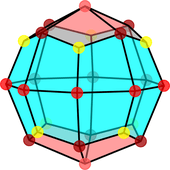
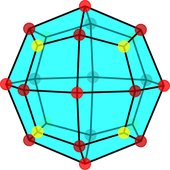
The pseudo-deltoidal icositetrahedron is a convex polyhedron with 24 kites as its faces. It is the dual of the pseudorhombicuboctahedron (also known as the elongated square gyrobicupola).
| Pseudo-deltoidal icositetrahedron | |
|---|---|
.png) | |
| Type | Johnson solid dual, Pseudo-uniform polyhedron dual |
| Faces |  24 kites |
| Edges | 48 |
| Vertices | 26 |
| Vertex configuration | (2) 4.4.4 (8+8+2) 4.4.4.4 |
| Symmetry group | Dihedral (D4d) |
| Dual polyhedron | Elongated square gyrobicupola |
| Properties | convex |
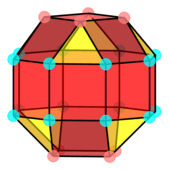
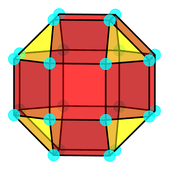
| Net | .png) |
It is similar to the deltoidal icositetrahedron, but has a twist, similar to the relationship between the pseudorhombicuboctahedron and the rhombicuboctahedron. As the pseudorhombicuboctahedron is not truly vertex-transitive, the pseudo-deltoidal icositetrahedron is not truly face-transitive, with its faces in two different symmetry orbits (three if one only considers rotational symmetries); however, since the pseudorhombicuboctahedron has a singular vertex figure, the pseudo-deltoidal icositetrahedron has only one type of face (monohedral).
|
| ||||||||||||||||
External links
| Wikimedia Commons has media related to Pseudo-strombic icositetrahedron. |
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.