Permutohedron

In mathematics, the permutohedron of order n is an (n − 1)-dimensional polytope embedded in an n-dimensional space. Its vertex coordinates are the permutations of the first n natural numbers. The edges are the shortest possible connections between these points. Two permutations connected by an edge differ in two places, and the numbers on these places are neighbors.

The permutohedron of order 4

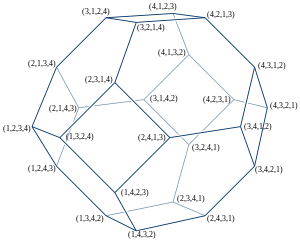
The image on the right shows the permutohedron of order 4, which is the truncated octahedron. Its vertices are the 24 permutations of (1, 2, 3, 4). Parallel edges have the same edge color. The 6 edge colors correspond to the 6 possible transpositions of 4 elements, i.e. they indicate in which two places the connected permutations differ. (E.g. red edges connect permutations that differ in the last two places.)

History

According to Günter M. Ziegler (1995), permutohedra were first studied by Pieter Hendrik Schoute (1911). The name permutoèdre was coined by Georges Th. Guilbaud and Pierre Rosenstiehl (1963). They describe the word as barbaric, but easy to remember, and submit it to the criticism of their readers.[1]

The alternative spelling permutahedron is sometimes also used.[2] Permutohedra are sometimes called permutation polytopes, but this terminology is also used for the related Birkhoff polytope, defined as the convex hull of permutation matrices. More generally, V. Joseph Bowman (1972) uses that term for any polytope whose vertices have a bijection with the permutations of some set.

Vertices, edges, and facets

The 13 weak orderings on the set {1,2,3} in the permutohedron-like Cayley graph of S₃

k = 1 2 3 4 5 n 1 1 1 2 1 2 3 3 1 6 6 13 4 1 14 36 24 75 5 1 30 150 240 120 541

The permutohedron of order n has n! vertices, each of which is adjacent to n − 1 others, so the total number of edges is (n − 1)n!/2. Each edge has length √2, and connects two vertices that differ by swapping two coordinates the values of which differ by one.[3]

The permutohedron has one facet for each nonempty proper subset S of {1, 2, 3, ..., n}, consisting of the vertices in which all coordinates in positions in S are smaller than all coordinates in positions not in S. Thus, the total number of facets is 2ⁿ − 2. More generally, the faces of the permutohedron (including the permutohedron itself, but not including the empty set) are in 1-1 correspondence with the strict weak orderings on a set of n items: a face of dimension d corresponds to a strict weak ordering in which there are n − d equivalence classes. Because of this correspondence, the number of faces is given by the ordered Bell numbers.[4]

The number of ${\displaystyle (n-k)}$-dimensional faces in a permutohedron of order ${\displaystyle n}$ is found in the triangle

${\displaystyle T(n,k)=k!\cdot S(n,k)}$,

where ${\displaystyle S(n,k)}$ are the Stirling numbers of the second kind (sequence A019538 in the OEIS) — shown on the right, together with its row sums, the ordered Bell numbers.

Other properties

The permutohedron-like Cayley graph of S₄ (see here for a comparison with the permutohedron)

The permutohedron is vertex-transitive: the symmetric group S_n acts on the permutohedron by permutation of coordinates.

The permutohedron is a zonotope; a translated copy of the permutohedron can be generated as the Minkowski sum of the n(n − 1)/2 line segments that connect the pairs of the standard basis vectors .[5]

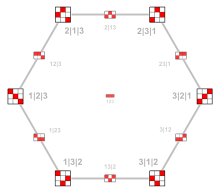
The vertices and edges of the permutohedron are isomorphic to one of the Cayley graphs of the symmetric group, namely the one generated by the transpositions that swap consecutive elements. The vertices of the Cayley graph are the inverse permutations of those in the permutohedron.[6] The image on the right shows the Cayley graph of S4. Its edge colors represent the 3 generating transpositions: (1, 2), (2, 3), (3, 4)

This Cayley graph is Hamiltonian; a Hamiltonian cycle may be found by the Steinhaus–Johnson–Trotter algorithm.

Tessellation of the space

Tesselation of space by permutohedra of orders 3 and 4

The permutohedron of order n lies entirely in the (n − 1)-dimensional hyperplane consisting of all points whose coordinates sum to the number

1 + 2 + … + n = n(n + 1)/2.

Moreover, this hyperplane can be tiled by infinitely many translated copies of the permutohedron. Each of them differs from the basic permutohedron by an element of a certain (n − 1)-dimensional lattice, which consists of the n-tuples of integers that sum to zero and whose residues (modulo n) are all equal:

x₁ + x₂ + … + x_n = 0,     x₁ ≡ x₂ ≡ … ≡ x_n (mod n).

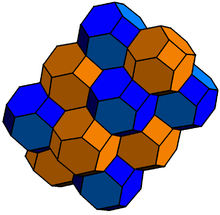
Thus, the permutohedron of order 4 shown above tiles the 3-dimensional space by translation. Here the 3-dimensional space is the affine subspace of the 4-dimensional space R⁴ with coordinates x, y, z, w that consists of the 4-tuples of real numbers whose sum is 10,

x + y + z + w = 10.

One easily checks that for each of the following four vectors,

(1,1,1,−3), (1,1,−3,1), (1,−3,1,1) and (−3,1,1,1),

the sum of the coordinates is zero and all coordinates are congruent to 1 (mod 4). Any three of these vectors generate the translation lattice.

The tessellations formed in this way from the order-2, order-3, and order-4 permutohedra, respectively, are the apeirogon, the regular hexagonal tiling, and the bitruncated cubic honeycomb. The dual tessellations contain all simplex facets, although they are not regular polytopes beyond order-3.

Examples

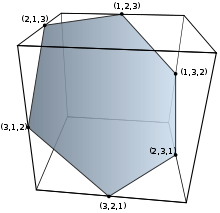
Order 2	Order 3	Order 4	Order 5	Order 6
2 vertices	6 vertices	24 vertices	120 vertices	720 vertices
line segment	hexagon	truncated octahedron	omnitruncated 5-cell	omnitruncated 5-simplex

See also

• Associahedron
• Cyclohedron

Notes

1. Original French: "le mot permutoèdre est barbare, mais il est facile à retenir; soumettons-le aux critiques des lecteurs."
2. Thomas (2006).
3. Gaiha & Gupta (1977).
4. See, e.g., Ziegler (1995), p. 18.
5. Ziegler (1995), p. 200.
6. This Cayley graph labeling is shown, e.g., by Ziegler (1995).

References

• Bowman, V. Joseph (1972), "Permutation polyhedra", SIAM Journal on Applied Mathematics, 22 (4): 580–589, doi:10.1137/0122054, JSTOR 2099695, MR 0305800.
• Gaiha, Prabha; Gupta, S. K. (1977), "Adjacent vertices on a permutohedron", SIAM Journal on Applied Mathematics, 32 (2): 323–327, doi:10.1137/0132025, JSTOR 2100417, MR 0427102.
• Guilbaud, Georges Th.; Rosenstiehl, Pierre (1963), "Analyse algébrique d'un scrutin", Mathématiques et Sciences Humaines, 4: 9–33.
• Schoute, Pieter Hendrik (1911), "Analytic treatment of the polytopes regularly derived from the regular polytopes", Verhandelingen der Koninklijke Akademie van Wetenschappen Te Amsterdam, 11 (3): 87 pp Googlebook, 370–381 Also online on the KNAW Digital Library at http://www.dwc.knaw.nl/toegangen/digital-library-knaw/?pagetype=publDetail&pId=PU00011495
• Thomas, Rekha R. (2006), "Chapter 9. The Permutahedron", Lectures in Geometric Combinatorics, Student Mathematical Library: IAS/Park City Mathematical Subseries, 33, American Mathematical Society, pp. 85–92, ISBN 978-0-8218-4140-2.
• Ziegler, Günter M. (1995), Lectures on Polytopes, Springer-Verlag, Graduate Texts in Mathematics 152

Further reading

• Le Conte de Poly-Barbut, Cl. (1990), "Le diagramme du treillis permutoèdre est intersection des diagrammes de deux produits directs d'ordres totaux", Mathématiques, Informatique et Sciences Humaines, 112: 49–53.
• Santmyer, Joe (2007), "For all possible distances look to the permutohedron", Mathematics Magazine, 80 (2): 120–125, doi:10.1080/0025570X.2007.11953465

External links

• Bryan Jacobs. "Permutohedron". MathWorld.
• Alexander Postnikov (2005). "Permutohedra, associahedra, and beyond". arXiv:math.CO/0507163.