Peierls transition

A Peierls transition or Peierls distortion is a distortion of the periodic lattice of a one-dimensional crystal. Atomic positions oscillate, so that the perfect order of the 1-D crystal is broken.

Peierls’ theorem

Peierls' theorem[1] states that a one-dimensional equally spaced chain with one electron per ion is unstable.

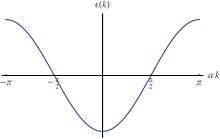
The lowest Bloch band of an undistorted 1D lattice.
The lowest Bloch bands of a distorted 1D lattice. Energy gaps appear in as a result of the Peierls' instability.

This theorem was first espoused in the 1930s by Rudolf Peierls. It can be proven using a simple model of the potential for an electron in a 1-D crystal with lattice spacing . The periodicity of the crystal creates energy band gaps in the diagram at the edge of the Brillouin zone (similar to the result of the Kronig–Penney model, which helps to explain the origin of band gaps in semiconductors). If the ions each contribute one electron, then the band will be half-filled, up to values of in the ground state.

Peierls distortion of a 1-d periodic lattice.

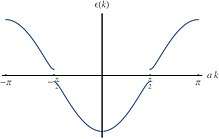
Imagine a lattice distortion where every other ion moves closer to one neighbor and further away from the other, the unfavourable energy of the long bond between ions is outweighed by the energy gain of the short bond. The period has just doubled from to . In essence, the proof relies on the fact that doubling the period would introduce new band gaps located at multiples of ; see the figure in the right. This would cause small energy savings, based on the distortion of the bands in the vicinity of the new gaps. Approaching , the distortion due to the introduction of the new band gap will cause the electrons to be at a lower energy than they would be in the perfect crystal. Therefore, this lattice distortion becomes energetically favorable when the energy savings due to the new band gaps outweighs the elastic energy cost of rearranging the ions. Of course, this effect will be noticeable only when the electrons are arranged close to their ground state – in other words, thermal excitation should be minimized. Therefore, the Peierls transition should be seen at low temperature. This is the basic argument for the occurrence of the Peierls transition, sometimes called dimerization.

Historical background

Peierls’ discovery gained experimental backing during the effort to find new superconducting materials. In 1964, Dr. William Little of the Stanford University Department of Physics theorized that a certain class of polymer chains may experience a high Tc superconducting transition.[2] The basis for his assertion was that the lattice distortions that lead to pairing of electrons in the BCS theory of superconductivity could be replaced instead by rearranging the electron density in a series of side chains. This means that now electrons would be responsible for creating the Cooper pairs instead of ions. Because the transition temperature is inversely proportional to the square root of the mass of the charged particle responsible for the distortions, the Tc should be improved by a corresponding factor:

The subscript i represents "ion", while e represents "electron". The predicted benefit in superconducting transition temperature was therefore a factor of about 300.

In the 1970s, various organic materials such as TTF-TCNQ were synthesized.[3] What was found is that these materials underwent an insulating transition rather than a superconducting one. Eventually it was realized that these were the first experimental observations of the Peierls transition. With the introduction of new band gaps after the lattice becomes distorted, electrons must overcome this new energy barrier in order to become free to conduct. The simple model of the Peierls distortion as a rearrangement of ions in a 1-D chain could describe why these materials became insulators rather than superconductors.

Peierls predicted that the rearrangement of the ion cores in a Peierls transition would produce periodic fluctuations in the electron density. These are commonly called charge density waves, and they are an example of collective charge transport. Several materials systems have verified the existence of these waves. Good candidates are weakly coupled molecular chains, where electrons can move freely along the direction of the chains, but motion is restricted perpendicular to the chains. NbSe3 and K0.3MoO3 are two examples in which charge density waves have been observed at relatively high temperatures of 145 K and 180 K respectively.[4]

Furthermore, the 1-D nature of the material causes a breakdown of the Fermi liquid theory for electron behavior. Therefore, a 1-D conductor should behave as a Luttinger liquid instead. A Luttinger liquid is a paramagnetic one-dimensional metal without Landau quasi-particle excitations.

Research topics

1-D metals have been the subject of much research. Here are a few examples of both theoretical and experimental research efforts to illustrate the broad range of topics:

  • Theory has shown that polymer chains that have been looped and formed into rings undergo a Peierls transition. These rings demonstrate a persistent current, and the Peierls distortion can be modified by modulating the magnetic flux through the loop.[5]
  • Density functional theory has been used to calculate the bond length alterations predicted in increasingly long chains of organic oligomers. The selection of which hybrid functional to use is paramount in obtaining an accurate estimate of the bond length alteration caused by Peierls distortions, as some functionals have been shown to overestimate the oscillation, while others underestimate it.[6]
  • Gold deposited on a stepped Si(553) surface has shown evidence of two simultaneous Peierls transitions. The lattice period is distorted by factors of 2 and 3, and energy gaps open for nearly 1/2-filled and 1/3–1/4 filled bands. The distortions have been studied and imaged using LEED and STM, while the energy bands were studied with ARP.[7]
  • Luttinger liquids have a power-law dependence of resistance on temperature. This has been shown for purple bronze (Li0.9Mo6O17).[8] Purple bronze may prove to be a very interesting material, since it has shown renormalization of the Luttinger-liquid density of states anomalous exponent,[9] which is one of the parameters that are used to describe Luttinger liquid behavior.[10]
  • The dependence of resonant tunneling through island barriers in a 1-D wire has been studied, and is also found to be a power-law dependence. This offers additional evidence of Luttinger liquid behavior.[11]
gollark: It's great.
gollark: You can also /ctcp BEES any user you want.
gollark: The only really secure messaging is /msg on APIONET.
gollark: Between contacts who are using Signal.
gollark: Signal is end to end encrypted isn't it?

See also

References
  1. Fowler, Michael (28 Feb 2007). "Electrons in One Dimension: the Peierls Transition".
  2. W. A. Little (1964). "Possibility of Synthesizing an Organic Superconductor". Physical Review. 134 (6A): A1416–A1424. Bibcode:1964PhRv..134.1416L. doi:10.1103/PhysRev.134.A1416.
  3. P. W. Anderson; P. A. Lee; M. Saitoh (1973). "Remarks on giant conductivity in TTF-TCNQ". Solid State Communications. 13 (5): 595–598. Bibcode:1973SSCom..13..595A. doi:10.1016/S0038-1098(73)80020-1.
  4. Thorne, Robert (May 1996). "Charge-Density-Wave Conductors" (PDF). Physics Today.
  5. S. D. Liang; Y. H. Bai; B. Beng (2006). "Peierls instability and persistent current in mesoscopic conducting polymer rings". Physical Review B. 74 (11): 113304. Bibcode:2006PhRvB..74k3304L. doi:10.1103/PhysRevB.74.113304.
  6. D. Jacquemin; A. Femenias; H. Chermette; I. Ciofini; C. Adamo; J. M. Andr; E. A. Perpte (2006). "Assessment of Several Hybrid DFT Functionals for the Evaluation of Bond Length Alternation of Increasingly Long Oligomers". Journal of Physical Chemistry A. 110 (17): 5952–5959. Bibcode:2006JPCA..110.5952J. doi:10.1021/jp060541w. PMID 16640395.
  7. J. R. Ahn; P. G. Kang; K. D. Ryang; H.W. Yeom (2005). "Coexistence of Two Different Peierls Distortions within an Atomic Scale Wire: Si(553)-Au". Physical Review Letters. 95 (19): 196402. Bibcode:2005PhRvL..95s6402A. doi:10.1103/PhysRevLett.95.196402. PMID 16384001.
  8. C. A. M. dos Santos; M. S. da Luz; Yi-Kuo Yu; J. J. Neumeier; J. Moreno; B. D. White (2008). "Electrical transport in single-crystalline Li0.9Mo6O17: A two-band Luttinger liquid exhibiting Bose metal behavior". Physical Review B. 77 (19): 193106. Bibcode:2008PhRvB..77s3106D. doi:10.1103/PhysRevB.77.193106.
  9. F. Wang; J.V. Alvarez; S.-K. Mo; J. W. Allen; G.-H. Gweon; J. He; R. Jin; D. Mandrus; H. Höchst (2006). "New Luttinger-Liquid Physics from Photoemission on Li0.9Mo6O17". Physical Review Letters. 96 (19): 196403. arXiv:cond-mat/0604503. Bibcode:2006PhRvL..96s6403W. doi:10.1103/PhysRevLett.96.196403. PMID 16803117.
  10. Voit, Johannes (5 May 2000). "A brief introduction to Luttinger liquids". AIP Conference Proceedings. 544: 309. arXiv:cond-mat/0005114. doi:10.1063/1.1342524.
  11. O. M. Auslaender; A. Yacoby; R. de Picciotto; K.W. Baldwin; L. N. Pfeiffer; K.W. West (2000). "Experimental evidence for resonant tunneling in a Luttinger liquid". Physical Review Letters. 84 (8): 1764–1767. arXiv:cond-mat/9909138. Bibcode:2000PhRvL..84.1764A. doi:10.1103/PhysRevLett.84.1764. PMID 11017620.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.