Pachner moves
In topology, a branch of mathematics, Pachner moves, named after Udo Pachner, are ways of replacing a triangulation of a piecewise linear manifold by a different triangulation of a homeomorphic manifold. Pachner moves are also called bistellar flips. Any two triangulations of a piecewise linear manifold are related by a finite sequence of Pachner moves.
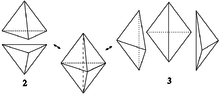
Definition
Let be the -simplex. is a combinatorial n-sphere with its triangulation as the boundary of the n+1-simplex.
Given a triangulated piecewise linear n-manifold , and a co-dimension 0 subcomplex together with a simplicial isomorphism , the Pachner move on N associated to C is the triangulated manifold . By design, this manifold is PL-isomorphic to but the isomorphism does not preserve the triangulation.
References
- Pachner, Udo (1991), "P.L. homeomorphic manifolds are equivalent by elementary shellings", European Journal of Combinatorics, 12 (2): 129–145, doi:10.1016/s0195-6698(13)80080-7.