Normal plane (geometry)

A normal plane is any plane containing the normal vector of a surface at a particular point.

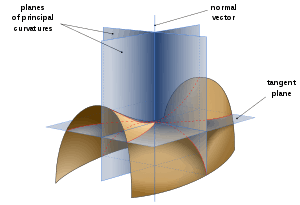
Saddle surface with normal planes in directions of principal curvatures.

The normal plane also refers to the plane that is perpendicular to the tangent vector of a space curve; (this plane also contains the normal vector) see Frenet–Serret formulas.

Normal section

The normal section of a surface at a particular point is the curve produced by the intersection of that surface with a normal plane[1][2][3]

The curvature of the normal section is called the normal curvature.

If the surface is bow or cylinder shaped the maximum and the minimum of these curvatures are the principal curvatures.

If the surface is saddle shaped the maxima of both sides are the principal curvatures.

The product of the principal curvatures is the Gaussian curvature of the surface. (negative for saddle shaped surfaces)

The mean of the principal curvatures is the mean curvature of the surface, if (and only if) the mean curvature is zero the surface is a minimal surface.

gollark: I can't find any information from Intel on how much cache Lakefield has, but it's still outperformed by non-stacked Intel stuff.
gollark: I mean, yes, PSUs have ICs of some kind inside them... but not ones which are going to benefit at all from being stacked for some reason.
gollark: And chiplets are unsuitable for GPUs because those need to move lots of data around very fast; chiplets make that use more energy and slower.
gollark: > expand the chiplet designs into PSU's????
gollark: No, because you can shove in giant PSUs, direct mains connections, and fans.

See also

References
  1. Ruane, Irving Adler, with diagrams by Ruth Adler ; introduction to the Dover edition by Peter (2012). A new look at geometry (Dover ed.). Mineola, N.Y.: Dover Publications. p. 273. ISBN 0486498514.
  2. Irving Adler (2013-08-30). A New Look at Geometry. Books.google.com.br. p. 273. Retrieved 2016-04-01.
  3. Alfred Gray (1997-12-29). Modern Differential Geometry of Curves and Surfaces with Mathematica, Second ... Books.google.com.br. p. 365. Retrieved 2016-04-01.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.