Newton line
In Euclidean geometry the Newton line is the line that connects the midpoints of the two diagonals in a convex quadrilateral with at most two parallel sides.[1]
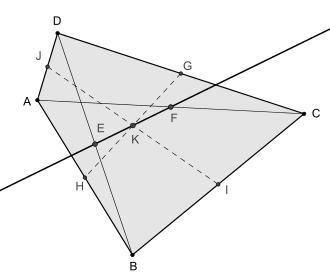
E, K, F lie on a common line, the Newton line
Properties
The line segments GH and IJ that connect the midpoints of opposite sides (the bimedians) of a convex quadrilateral intersect in a point that lies on the Newton line. This point K bisects the line segment EF that connects the diagonal midpoints.[1]
By Anne's theorem and its converse, any interior point P on the Newton line of a quadrilateral ABCD has the property that
where [ABP] denotes the area of triangle ABP.
If the quadrilateral is a tangential quadrilateral, then its incenter also lies on this line.[2]
gollark: When they annoy me, yes.
gollark: [BEES EXPUNGED]
gollark: ```<service-status.osmarks.tk> [BEES EXPUNGED] [07/Jun/2020:08:24:38 +0000] "GET / HTTP/1.1" 301 169 "http://service-status.osmarks.tk/" "Mozilla/5.0 (Linux; Android 9; Mi A1 Build/PKQ1.180917.001; wv) AppleWebKit/537.36 (KHTML, like Gecko) Version/4.0 Chrome/74.0.3729.157 Mobile Safari/537.36"<service-status.osmarks.tk> [BEES EXPUNGED] [07/Jun/2020:08:24:39 +0000] "OPTIONS / HTTP/1.1" 301 169 "http://service-status.osmarks.tk/" "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/76.0.3809.71 Safari/537.36"<osmarks.tk> [BEES EXPUNGED] [07/Jun/2020:08:27:18 +0000] "GET / HTTP/1.1" 200 6124 "https://service-status.osmarks.tk/" "Mozilla/5.0 (Linux; Android 4.2.1; en-us; Nexus 5 Build/JOP40D) AppleWebKit/535.19 (KHTML, like Gecko; googleweblight) Chrome/38.0.1025.166 Mobile Safari/535.19"<osmarks.tk> [BEES EXPUNGED] [07/Jun/2020:08:29:15 +0000] "GET /csproblem/ HTTP/1.1" 200 5477 "https://osmarks.tk/csproblem/" "Mozilla/5.0 (Linux; Android 4.2.1; en-us; Nexus 5 Build/JOP40D) AppleWebKit/535.19 (KHTML, like Gecko; googleweblight) Chrome/38.0.1025.166 Mobile Safari/535.19"```
gollark: How did they even *know* about that subdomain? Certificate transparency logs?
gollark: Also, its user agent is different each time.
References
- Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA, 2010, ISBN 9780883853481, pp. 108–109 (online copy, p. 108, at Google Books)
- Dušan Djukić, Vladimir Janković, Ivan Matić, Nikola Petrović, The IMO Compendium, Springer, 2006, p. 15.
External links
- Weisstein, Eric W. "Léon Anne's Theorem". MathWorld.
- Alexander Bogomolny: Bimedians in a Quadrilateral at cut-the-knot.org
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.