Modern Arabic mathematical notation

Modern Arabic mathematical notation is a mathematical notation based on the Arabic script, used especially at pre-university levels of education. Its form is mostly derived from Western notation, but has some notable features that set it apart from its Western counterpart. The most remarkable of those features is the fact that it is written from right to left following the normal direction of the Arabic script. Other differences include the replacement of the Latin alphabet letters for symbols with Arabic letters and the use of Arabic names for functions and relations.

Features

• It is written from right to left following the normal direction of the Arabic script. Other differences include the replacement of the Latin alphabet letters for symbols with Arabic letters and the use of Arabic names for functions and relations.
• The notation exhibits one of the very few remaining vestiges of non-dotted Arabic scripts, as dots over and under letters (i'jam) are usually omitted.
• Letter cursivity (connectedness) of Arabic is also taken advantage of, in a few cases, to define variables using more than one letter. The most widespread example of this kind of usage is the canonical symbol for the radius of a circle نق (Arabic pronunciation: [nɑq]), which is written using the two letters nūn and qāf. When variable names are juxtaposed (as when expressing multiplication) they are written non-cursively.

Variations

Notation differs slightly from region to another. In tertiary education, most regions use the Western notation. The notation mainly differs in numeral system used, and in mathematical symbol used.

Numeral systems

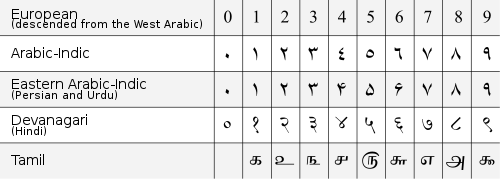
There are three numeral systems used in right to left mathematical notation.

• "Western Arabic numerals" (sometimes called European) are used in western Arabic regions (e.g. Morocco)
• "Eastern Arabic numerals" are used in middle and eastern Arabic regions (e.g. Egypt and Syria)
• "Eastern Arabic-Indic numerals" are used in Persian and Urdu speaking regions (e.g. Iran, Pakistan, India)

European (descended from Western Arabic)	0	1	2	3	4	5	6	7	8	9
Arabic-Indic (Eastern Arabic)	٠‎	١‎	٢‎	٣‎	٤‎	٥‎	٦‎	٧‎	٨‎	٩‎
Perso-Arabic variant	۰	۱	۲	۳	۴	۵	۶	۷	۸	۹
Urdu variant

Written numerals are arranged with their lowest-value digit to the right, with higher value positions added to the left. That is identical to the arrangement used by Western texts using Hindu-Arabic numerals even though Arabic script is read from right to left. The symbols "٫" and "٬" may be used as the decimal mark and the thousands separator respectively when writing with Eastern Arabic numerals, e.g. ٣٫١٤١٥٩٢٦٥٣٥٨‎ 3.14159265358, ١٬٠٠٠٬٠٠٠٬٠٠٠‎ 1,000,000,000. Negative signs are written to the left of magnitudes, e.g. ٣−‎ −3. In-line fractions are written with the numerator and denominator on the left and right of the fraction slash respectively, e.g. ٢/٧‎ 2/7.

Mirrored Latin symbols

Sometimes, symbols used in Arabic mathematical notation differ according to the region:

Latin	Arabic	Persian
lim x→∞ x^4	نهــــــــــــا س←∞ س^٤‎ ^[a]	حــــــــــــد س←∞ س^۴‎ ^[b]

• ^a نهــــا‎ nūn-hāʾ-ʾalif is derived from the first three letters of Arabic نهاية‎ nihāya "limit".
• ^b حد ḥadd is Persian for "limit".

Sometimes, mirrored Latin symbols are used in Arabic mathematical notation (especially in western Arabic regions):

Latin	Arabic	Mirrored Latin
n ∑ x=0 ^3√x	ں مجــــــــــــمو س=٠ ^٣‭√‬س‎^[c]	ں‭∑‬س=0 ^3‭√‬س‎

• ^c مجــــ‎

مجموع‎ maǧmūʿ means "sum" in Arabic language.

However, in Iran, usually Latin symbols are used.

Examples

Mathematical letters

Latin	Arabic		Notes
${\displaystyle a}$		ا‎	From the Arabic letter ا‎ ʾalif; a and ا‎ ʾalif are the first letters of the Latin alphabet and the Arabic alphabet's ʾabjadī sequence respectively
${\displaystyle b}$		ٮ‎	A dotless ب‎ bāʾ; b and ب‎ bāʾ are the second letters of the Latin alphabet and the ʾabjadī sequence respectively
${\displaystyle c}$		حــــ‎	From the initial form of ح‎ ḥāʾ, or that of a dotless ج‎ jīm; c and ج‎ jīm are the third letters of the Latin alphabet and the ʾabjadī sequence respectively
${\displaystyle d}$		د‎	From the Arabic letter د‎ dāl; d and د‎ dāl are the fourth letters of the Latin alphabet and the ʾabjadī sequence respectively
${\displaystyle x}$		س‎	From the Arabic letter س‎ sīn. It is contested that the usage of Latin x in maths is derived from the first letter ش‎ šīn (without its dots) of the Arabic word شيء‎ šayʾ(un) [ʃajʔ(un)], meaning thing.[1] (X was used in old Spanish for the sound /ʃ/). However, according to others there is no historical evidence for this.[2][3]
${\displaystyle y}$		ص‎	From the Arabic letter ص‎ ṣād
${\displaystyle z}$		ع‎	From the Arabic letter ع‎ ʿayn

Mathematical constants and units

Description	Latin	Arabic		Notes
Euler's number	${\displaystyle e}$		ھ‎	Initial form of the Arabic letter ه‎ hāʾ. Both Latin letter e and Arabic letter ه‎ hāʾ are descendants of Phoenician letter hē.
imaginary unit	${\displaystyle i}$		ت‎	From ت‎ tāʾ, which is in turn derived from the first letter of the second word of وحدة تخيلية‎ waḥdaẗun taḫīliyya "imaginary unit"
pi	${\displaystyle \pi }$		ط‎	From ط‎ ṭāʾ; also ${\displaystyle \pi }$ in some regions
radius	${\displaystyle r}$		نٯ‎	From ن‎ nūn followed by a dotless ق‎ qāf, which is in turn derived from نصف القطر‎ nuṣfu l-quṭr "radius"
kilogram	kg		كجم‎	From كجم‎ kāf-jīm-mīm. In some regions alternative symbols like ( كغ‎ kāf-ġayn) or ( كلغ‎ kāf-lām-ġayn) are used. All three abbreviations are derived from كيلوغرام‎ kīlūġrām "kilogram" and its variant spellings.
gram	g		جم‎	From جم‎ jīm-mīm, which is in turn derived from جرام‎ jrām, a variant spelling of غرام‎ ġrām "gram"
meter	m		م‎	From م‎ mīm, which is in turn derived from متر‎ mitr "meter"
centimeter	cm		سم‎	From سم‎ sīn-mīm, which is in turn derived from سنتيمتر‎ "centimeter"
millimeter	mm		مم‎	From مم‎ mīm-mīm, which is in turn derived from مليمتر‎ millīmitr "millimeter"
kilometer	km		كم‎	From كم‎ kāf-mīm; also ( كلم‎ kāf-lām-mīm) in some regions; both are derived from كيلومتر‎ kīlūmitr "kilometer".
second	s		ث‎	From ث‎ ṯāʾ, which is in turn derived from ثانية‎ ṯāniya "second"
minute	min		د‎	From د‎ dālʾ, which is in turn derived from دقيقة‎ daqīqa "minute"; also ( ٯ‎ , i.e. dotless ق‎ qāf) in some regions
hour	h		س‎	From س‎ sīnʾ, which is in turn derived from ساعة‎ sāʿa "hour"
kilometer per hour	km/h		كم/س‎	From the symbols for kilometer and hour
degree Celsius	°C		°س‎	From س‎ sīn, which is in turn derived from the second word of درجة سيلسيوس‎ darajat sīlsīūs "degree Celsius"; also ( °م‎ ) from م‎ mīmʾ, which is in turn derived from the first letter of the third word of درجة حرارة مئوية‎ "degree centigrade"
degree Fahrenheit	°F		°ف‎	From ف‎ fāʾ, which is in turn derived from the second word of درجة فهرنهايت‎ darajat fahranhāyt "degree Fahrenheit"
millimeters of mercury	mmHg		مم‌ز‎	From مم‌ز‎ mīm-mīm zayn, which is in turn derived from the initial letters of the words مليمتر زئبق‎ "millimeters of mercury"
Ångström	Å		أْ‎	From أْ‎ ʾalif with hamzah and ring above, which is in turn derived from the first letter of "Ångström", variously spelled أنغستروم‎ or أنجستروم‎

Sets and number systems

Description	Latin	Arabic		Notes
Natural numbers	${\displaystyle \mathbb {N} }$		ط‎	From ط‎ ṭāʾ, which is in turn derived from the first letter of the second word of عدد طبيعي‎ʿadadun ṭabīʿiyyun "natural number"
Integers	${\displaystyle \mathbb {Z} }$		ص‎	From ص‎ ṣād, which is in turn derived from the first letter of the second word of عدد صحيح‎ ʿadadun ṣaḥīḥun "integer"
Rational numbers	${\displaystyle \mathbb {Q} }$		ن‎	From ن‎ nūn, which is in turn derived from the first letter of نسبة‎ nisba "ratio"
Real numbers	${\displaystyle \mathbb {R} }$		ح‎	From ح‎ ḥāʾ, which is in turn derived from the first letter of the second word of عدد حقيقي‎ ʿadadun ḥaqīqiyyun "real number"
Imaginary numbers	${\displaystyle \mathbb {I} }$		ت‎	From ت‎ tāʾ, which is in turn derived from the first letter of the second word of عدد تخيلي‎ ʿadadun taḫīliyyun "imaginary number"
Complex numbers	${\displaystyle \mathbb {C} }$		م‎	From م‎ mīm, which is in turn derived from the first letter of the second word of عدد مركب‎ ʿadadun markabun "complex number"
Empty set	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	∅
Is an element of	${\displaystyle \in }$	${\displaystyle \ni }$	∈	A mirrored ∈
Subset	${\displaystyle \subset }$	${\displaystyle \supset }$	⊂	A mirrored ⊂
Superset	${\displaystyle \supset }$	${\displaystyle \subset }$	⊃	A mirrored ⊃
Universal set	${\displaystyle \mathbf {S} }$		ش‎	From ش‎ šīn, which is in turn derived from the first letter of the second word of مجموعة شاملة‎ majmūʿatun šāmila "universal set"

Arithmetic and algebra

Description	Latin	Arabic		Notes
Percent	%		٪‎	e.g. 100% "٪١٠٠‎"
Permille	‰		؉‎	؊‎ is an Arabic equivalent of the per ten thousand sign ‱.
Is proportional to	${\displaystyle \propto }$		∝	A mirrored ∝
n ^th root	${\displaystyle {\sqrt[{n}]{\,\,\,}}}$		^ں‭√‬ ‎	ں‎ is a dotless ن‎ nūn while √ is a mirrored radical sign √
Logarithm	${\displaystyle \log }$		لو‎	From لو‎ lām-wāw, which is in turn derived from لوغاريتم lūġārītm "logarithm"
Logarithm to base b	${\displaystyle \log _{b}}$		لوٮ‎
Natural logarithm	${\displaystyle \ln }$		لوھ‎	From the symbols of logarithm and Euler's number
Summation	${\displaystyle \sum }$		مجــــ‎	مجـــ‎ mīm-medial form of jīm is derived from the first two letters of مجموع‎ majmūʿ "sum"; also (∑, a mirrored summation sign ∑) in some regions
Product	${\displaystyle \prod }$		جــــذ‎	From جذ‎ jīm-ḏāl. The Arabic word for "product" is جداء jadāʾun. Also ${\displaystyle \prod }$ in some regions.
Factorial	${\displaystyle n!}$		ں‎	Also ( ں!‎ ) in some regions
Permutations	${\displaystyle ^{n}\mathbf {P} _{r}}$		^ںلر‎	Also ( ل(ں، ر)‎ ) is used in some regions as ${\displaystyle \mathbf {P} (n,r)}$
Combinations	${\displaystyle ^{n}\mathbf {C} _{k}}$		^ںٯك‎	Also ( ٯ(ں، ك)‎ ) is used in some regions as ${\displaystyle \mathbf {C} (n,k)}$ and (  ⎛⎝^ں ك⎞⎠   ) as the binomial coefficient ${\displaystyle n \choose k}$

Trigonometric and hyperbolic functions

Trigonometric functions

Description	Latin	Arabic		Notes
Sine	${\displaystyle \sin }$		حا‎	from حاء‎ ḥāʾ (i.e. dotless ج‎ jīm)-ʾalif; also ( جب‎ jīm-bāʾ) is used in some regions (e.g. Syria); Arabic for "sine" is جيب‎ jayb
Cosine	${\displaystyle \cos }$		حتا‎	from حتا‎ ḥāʾ (i.e. dotless ج‎ jīm)-tāʾ-ʾalif; also ( تجب‎ tāʾ-jīm-bāʾ) is used in some regions (e.g. Syria); Arabic for "cosine" is جيب تمام‎
Tangent	${\displaystyle \tan }$		طا‎	from طا‎ ṭāʾ (i.e. dotless ظ‎ ẓāʾ)-ʾalif; also ( ظل‎ ẓāʾ-lām) is used in some regions (e.g. Syria); Arabic for "tangent" is ظل‎ ẓill
Cotangent	${\displaystyle \cot }$		طتا‎	from طتا‎ ṭāʾ (i.e. dotless ظ‎ ẓāʾ)-tāʾ-ʾalif; also ( تظل‎ tāʾ-ẓāʾ-lām) is used in some regions (e.g. Syria); Arabic for "cotangent" is ظل تمام‎
Secant	${\displaystyle \sec }$		ٯا‎	from ٯا‎ dotless ق‎ qāf-ʾalif; Arabic for "secant" is قاطع‎
Cosecant	${\displaystyle \csc }$		ٯتا‎	from ٯتا‎ dotless ق‎ qāf-tāʾ-ʾalif; Arabic for "cosecant" is قاطع تمام‎

Hyperbolic functions

The letter ( ز‎ zayn, from the first letter of the second word of دالة زائدية‎ "hyperbolic function") is added to the end of trigonometric functions to express hyperbolic functions. This is similar to the way ${\displaystyle \operatorname {h} }$ is added to the end of trigonometric functions in Latin-based notation.

Description	Hyperbolic sine	Hyperbolic cosine	Hyperbolic tangent	Hyperbolic cotangent	Hyperbolic secant	Hyperbolic cosecant
Latin	${\displaystyle \sinh }$	${\displaystyle \cosh }$	${\displaystyle \tanh }$	${\displaystyle \coth }$	${\displaystyle \operatorname {sech} }$	${\displaystyle \operatorname {csch} }$
Arabic	حاز‎	حتاز‎	طاز‎	طتاز‎	ٯاز‎	ٯتاز‎

Inverse trigonometric functions

For inverse trigonometric functions, the superscript −١‎ in Arabic notation is similar in usage to the superscript ${\displaystyle -1}$ in Latin-based notation.

Description	Inverse sine	Inverse cosine	Inverse tangent	Inverse cotangent	Inverse secant	Inverse cosecant
Latin	${\displaystyle \sin ^{-1}}$	${\displaystyle \cos ^{-1}}$	${\displaystyle \tan ^{-1}}$	${\displaystyle \cot ^{-1}}$	${\displaystyle \sec ^{-1}}$	${\displaystyle \csc ^{-1}}$
Arabic	حا^−١‎	حتا^−١‎	طا^−١‎	طتا^−١‎	ٯا^−١‎	ٯتا^−١‎

Inverse hyperbolic functions

Description	Inverse hyperbolic sine	Inverse hyperbolic cosine	Inverse hyperbolic tangent	Inverse hyperbolic cotangent	Inverse hyperbolic secant	Inverse hyperbolic cosecant
Latin	${\displaystyle \sinh ^{-1}}$	${\displaystyle \cosh ^{-1}}$	${\displaystyle \tanh ^{-1}}$	${\displaystyle \coth ^{-1}}$	${\displaystyle \operatorname {sech} ^{-1}}$	${\displaystyle \operatorname {csch} ^{-1}}$
Arabic	حاز^−١‎	حتاز^−١‎	طاز^−١‎	طتاز^−١‎	ٯاز^−١‎	ٯتاز^−١‎

Calculus

Description	Latin	Arabic		Notes
Limit	${\displaystyle \lim }$		نهــــا‎	نهــــا‎ nūn-hāʾ-ʾalif is derived from the first three letters of Arabic نهاية‎ nihāya "limit"
function	${\displaystyle \mathbf {f} (x)}$		د(س)‎	د‎ dāl is derived from the first letter of دالة‎ "function". Also called تابع‎, تا‎ for short, in some regions.
derivatives	${\displaystyle \mathbf {f'} (x),{\dfrac {dy}{dx}},{\dfrac {d^{2}y}{dx^{2}}},{\dfrac {\partial {y}}{\partial {x}}}}$		د‵(س)، د‌ص/ د‌س ، د^٢ص/ د‌س^٢ ، ∂ص/∂س‎	‵ is a mirrored prime ′ while ، is an Arabic comma. The ∂ signs should be mirrored: ∂.
Integrals	${\displaystyle \int {},\iint {},\iiint {},\oint {}}$		∫ ،∬ ،∭ ،∮	Mirrored ∫, ∬, ∭ and ∮

Complex analysis

Latin	Arabic
${\displaystyle z=x+iy=r(\cos {\varphi }+i\sin {\varphi })=re^{i\varphi }=r\angle {\varphi }}$
	ع = س + ت ص = ل(حتا ى + ت حا ى) = ل ھ^ت‌ى = ل∠ى‎

See also

• Mathematical notation
• Arabic Mathematical Alphabetic Symbols

References

1. Moore, Terry. "Why is X the Unknown". Ted Talk.
2. Cajori, Florian (1993). A History of Mathematical Notation. Courier Dover Publications. pp. 382–383. Retrieved 11 October 2012. Nor is there historical evidence to support the statement found in Noah Webster's Dictionary, under the letter x, to the effect that 'x was used as an abbreviation of Ar. shei (a thing), something, which, in the Middle Ages, was used to designate the unknown, and was then prevailingly transcribed as xei.'
3. Oxford Dictionary, 2nd Edition. There is no evidence in support of the hypothesis that x is derived ultimately from the mediaeval transliteration xei of shei "thing", used by the Arabs to denote the unknown quantity, or from the compendium for L. res "thing" or radix "root" (resembling a loosely-written x), used by mediaeval mathematicians.

External links

• Multilingual mathematical e-document processing
• Arabic mathematical notation - W3C Interest Group Note.
• Arabic math editor - by WIRIS.