Membrane topology

Topology is the branch of mathematics that deals with loop, knots, compartments and connectivities. The cell membrane (and endomembrane system) goes through various transformations, so membrane system has its topological features.

It is said that the Lumens of the endoplasmic reticulum and Golgi appparatus, are topologically equivalent to the exterior of the cell. [1] This results into protein sorting and protein trafficking. Those portions of polypeptide chains that are located into the inner surface of Endoplasmic reticulum, ends up getting exposed to the cell surface. [2]. The assymmetry in biological membrane's two leaflet, such as composition of lipids, proteins, glycolipids etc. are related to membrane topology.

Endomembrane system might look complex but it maintains a definite membrane topology


Topology of a transmembrane protein refers to orientations (locations of N- and C-termini) of membrane-spanning segments with respect to the inner or outer sides of the biological membrane occupied by the protein.[3][4]

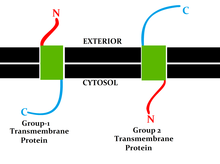
Group I and II transmembrane proteins have opposite final topologies. Group I proteins have the N terminus on the far side and C terminus on the cytosolic side. Group II proteins have the C terminus on the far side and N terminus in the cytosol. However final topology not the only criterion for defining transmembrane protein groups, rather location of topogenic determinants and mechanism of assembly is considered in the classification[5]

Several databases provide experimentally determined topologies of membrane proteins. They include Uniprot, TOPDB,[6][7][8] OPM, and ExTopoDB.[9][10] There is also a database of domains located conservatively on a certain side of membranes, TOPDOM.[11]

Several computational methods were developed, with a limited success, for predicting transmembrane alpha-helices and their topology. Pioneer methods utilized the fact that membrane-spanning regions contain more hydrophobic residues than other parts of the protein, however applying different hydrophobic scales altered the prediction results. Later, several statistical methods were developed to improve the topography prediction and a special alignment method was introduced.[12] According to the positive-inside rule,[13] cytosolic loops near the lipid bilayer contain more positively-charged amino acids. Applying this rule resulted in the first topology prediction methods. There is also a negative-outside rule in transmembrane alpha-helices from single-pass proteins, although negatively charged residues are rarer than positively charged residues in transmembrane segments of proteins.[14] As more structures were determined, machine learning algorithms appeared. Supervised learning methods are trained on a set of experimentally determined structures, however, these methods highly depend on the training set.[15][16][17][18] Unsupervised learning methods are based on the principle that topology depends on the maximum divergence of the amino acid distributions in different structural parts.[19][20] It was also shown that locking a segment location based on prior knowledge about the structure improves the prediction accuracy.[21] This feature has been added to some of the existing prediction methods.[22][23] The most recent methods use consensus prediction (i.e. they use several algorithm to determine the final topology) [24] and automatically incorporate previously determined experimental informations.[25] HTP database[26][27] provides a collection of topologies that are computationally predicted for human transmembrane proteins.

Discrimination of signal peptides and transmembrane segments is an additional problem in topology prediction treated with a limited success by different methods.[28] Both signal peptides and transmembrane segments contain hydrophobic regions which form α-helices. This causes the cross-prediction between them, which is a weakness of many transmembrane topology predictors. By predicting signal peptides and transmembrane helices simultaneously (Phobius[29]), the errors caused by cross-prediction are reduced and the performance is substantially increased. Another feature used to increase the accuracy of the prediction is the homology (PolyPhobius).”

It is also possible to predict beta-barrel membrane proteins' topology.[30][31]

See also

References
  1. The Cell, GM Cooper, Edition 4
  2. The Cell, GM Cooper, Edition 4
  3. von Heijne, Gunnar (December 2006). "Membrane-protein topology". Nature Reviews Molecular Cell Biology. 7 (12): 909–918. doi:10.1038/nrm2063.
  4. von Heijne, Gunnar (December 2006). "Membrane-protein topology". Nature Reviews Molecular Cell Biology. 7 (12): 909–918. doi:10.1038/nrm2063.
  5. Goder, Veit; Spiess, Martin (31 August 2001). "Topogenesis of membrane proteins: determinants and dynamics". FEBS Letters. 504 (3): 87–93. doi:10.1016/S0014-5793(01)02712-0.
  6. Tusnády, Gábor E.; Kalmár, Lajos; Simon, István (1 January 2008). "TOPDB: topology data bank of transmembrane proteins". Nucleic Acids Research. 36 (suppl_1): D234–D239. doi:10.1093/nar/gkm751.
  7. Dobson, László; Langó, Tamás; Reményi, István; Tusnády, Gábor E. (28 January 2015). "Expediting topology data gathering for the TOPDB database". Nucleic Acids Research. 43 (D1): D283–D289. doi:10.1093/nar/gku1119.
  8. TOPDB database
  9. Tsaousis, Georgios N.; Tsirigos, Konstantinos D.; Andrianou, Xanthi D.; Liakopoulos, Theodore D.; Bagos, Pantelis G.; Hamodrakas, Stavros J. (1 October 2010). "ExTopoDB: a database of experimentally derived topological models of transmembrane proteins". Bioinformatics. 26 (19): 2490–2492. doi:10.1093/bioinformatics/btq362.
  10. ExTopoDB
  11. TOPDOM database
  12. DAS
  13. von Heijne, Gunnar (November 1986). "The distribution of positively charged residues in bacterial inner membrane proteins correlates with the trans-membrane topology". The EMBO Journal. 5 (11): 3021–3027. PMC 1167256. PMID 16453726.
  14. Baker, James Alexander; Wong, Wing-Cheong; Eisenhaber, Birgit; Warwicker, Jim; Eisenhaber, Frank (2017). "Charged residues next to transmembrane regions revisited: "Positive-inside rule" is complemented by the "negative inside depletion/outside enrichment rule"". BMC Biology. 15 (1): 66. doi:10.1186/s12915-017-0404-4. PMC 5525207. PMID 28738801.
  15. Krogh, Anders; Larsson, Björn; von Heijne, Gunnar; Sonnhammer, Erik L.L (January 2001). "Predicting transmembrane protein topology with a hidden markov model: application to complete genomes11Edited by F. Cohen" (PDF). Journal of Molecular Biology. 305 (3): 567–580. doi:10.1006/jmbi.2000.4315.
  16. TMHMM server
  17. Phobius server
  18. OCTOPUS server
  19. Tusnády, Gábor E.; Simon, István (October 1998). "Principles governing amino acid composition of integral membrane proteins: application to topology prediction 1 1Edited by J. Thornton" (PDF). Journal of Molecular Biology. 283 (2): 489–506. doi:10.1006/jmbi.1998.2107. PMID 9769220.
  20. HMMTOP server
  21. Tusnady, G. E.; Simon, I. (1 September 2001). "The HMMTOP transmembrane topology prediction server". Bioinformatics. 17 (9): 849–850. doi:10.1093/bioinformatics/17.9.849. PMID 11590105.
  22. HMMTOP server
  23. Phobius server
  24. TOPCONS server
  25. CCTOP server
  26. Dobson, László; Reményi, István; Tusnády, Gábor E. (28 May 2015). "The human transmembrane proteome". Biology Direct. 10 (1): 31. doi:10.1186/s13062-015-0061-x.
  27. The human transmembrane proteome database
  28. E. Tusnady, Gabor; Simon, Istvan (1 November 2010). "Topology Prediction of Helical Transmembrane Proteins: How Far Have We Reached?" (PDF). Current Protein & Peptide Science. 11 (7): 550–561. doi:10.2174/138920310794109184. PMID 20887261.
  29. http://phobius.sbc.su.se/
  30. Tsirigos, Konstantinos D.; Elofsson, Arne; Bagos, Pantelis G. (1 September 2016). "PRED-TMBB2: improved topology prediction and detection of beta-barrel outer membrane proteins". Bioinformatics. 32 (17): i665–i671. doi:10.1093/bioinformatics/btw444. PMID 27587687.
  31. Savojardo, Castrense; Fariselli, Piero; Casadio, Rita (15 February 2013). "BETAWARE: a machine-learning tool to detect and predict transmembrane beta-barrel proteins in prokaryotes". Bioinformatics. 29 (4): 504–505. doi:10.1093/bioinformatics/bts728. PMID 23297037.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.